第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1. 如图,点D在△ABC的边AB上,DE交AC于点E,∠ADE = ∠B,点F在AD上,且AD² = AF·AB.
求证:(1)$\frac{AD}{AB}=\frac{AE}{AC}$;
(2)△AEF∽△ACD.
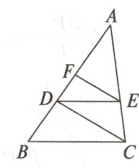
求证:(1)$\frac{AD}{AB}=\frac{AE}{AC}$;
(2)△AEF∽△ACD.

答案:
证明:
(1)
∵∠ADE=∠B,
∴DE//BC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$.
(2)
∵AD²=AF.AB,
∴$\frac{AD}{AB}$=$\frac{AF}{AD}$
由
(1),得$\frac{AD}{AB}$=$\frac{AE}{AC}$,
∴$\frac{AE}{AC}$=$\frac{AF}{AD}$.
∵∠A=∠A,
∴△AEF∽△ACD.
(1)
∵∠ADE=∠B,
∴DE//BC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$.
(2)
∵AD²=AF.AB,
∴$\frac{AD}{AB}$=$\frac{AF}{AD}$
由
(1),得$\frac{AD}{AB}$=$\frac{AE}{AC}$,
∴$\frac{AE}{AC}$=$\frac{AF}{AD}$.
∵∠A=∠A,
∴△AEF∽△ACD.
2. 如图,在四边形ABCD中,AC与BD相交于点O,直线l平行于BD,且与AB,DC,BC,AD及AC的延长线分别相交于点M,N,R,S和P. 求证:PM·PN = PR·PS.
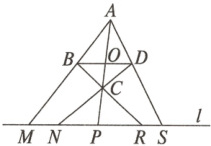

答案:
证明:
∵直线L//BD,
∴$\frac{PN}{OD}$=$\frac{CP}{CO}$=$\frac{PR}{OB}$,得$\frac{PN}{PR}$-$\frac{OD}{OB}$①,
$\frac{PM}{OB}$=$\frac{AP}{AO}$=$\frac{PS}{OD}$,得$\frac{PS}{PM}$=$\frac{OD}{OB}$②,
由①②,得$\frac{PN}{PR}$=$\frac{PS}{PM}$,即PM.PN=PR.PS.
∵直线L//BD,
∴$\frac{PN}{OD}$=$\frac{CP}{CO}$=$\frac{PR}{OB}$,得$\frac{PN}{PR}$-$\frac{OD}{OB}$①,
$\frac{PM}{OB}$=$\frac{AP}{AO}$=$\frac{PS}{OD}$,得$\frac{PS}{PM}$=$\frac{OD}{OB}$②,
由①②,得$\frac{PN}{PR}$=$\frac{PS}{PM}$,即PM.PN=PR.PS.
3. 如图1,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.
(1)求证:PE·PF = PC²;
(2)如图2,连接AC交BD于点O,连接OE,若CE⊥BC,求证:△POC∽△AEC.
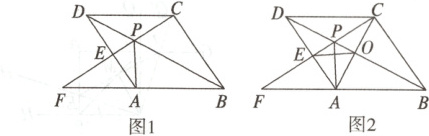
(1)求证:PE·PF = PC²;
(2)如图2,连接AC交BD于点O,连接OE,若CE⊥BC,求证:△POC∽△AEC.

答案:
证明:
(1)
∵四边形ABCD是菱形,
∴AD=CD,∠CDP=∠ADP,CD//AB.
CD=AD,
在△CDP和△ADP中,{∠CDP=∠ADP,
DP=DP,
∴△CDP≌△ADP(SAS),
∴PC=PA,∠DCP=∠DAP.
∵CD//AB,
∴∠DCP=∠F,
∴∠DAP=∠F.
∵∠APE=∠FPA,
∴△PAE∽△PFA,
∴$\frac{PA}{PF}$=$\frac{PE}{AP}$,
∴PA²=PE.PF,
∴PE.PF=PC².
(2)
∵CE⊥BC,
∴∠ECB=90°.
∵四边形ABCD是菱形,
∴AC⊥BD,AD//BC,
∠COP=90°,∠AEC=180°−∠BCE=180°−90°=90°,
∴∠COP=∠CEA.
∵∠OCP=∠ECA,
∴△POC∽△AEC.
(1)
∵四边形ABCD是菱形,
∴AD=CD,∠CDP=∠ADP,CD//AB.
CD=AD,
在△CDP和△ADP中,{∠CDP=∠ADP,
DP=DP,
∴△CDP≌△ADP(SAS),
∴PC=PA,∠DCP=∠DAP.
∵CD//AB,
∴∠DCP=∠F,
∴∠DAP=∠F.
∵∠APE=∠FPA,
∴△PAE∽△PFA,
∴$\frac{PA}{PF}$=$\frac{PE}{AP}$,
∴PA²=PE.PF,
∴PE.PF=PC².
(2)
∵CE⊥BC,
∴∠ECB=90°.
∵四边形ABCD是菱形,
∴AC⊥BD,AD//BC,
∠COP=90°,∠AEC=180°−∠BCE=180°−90°=90°,
∴∠COP=∠CEA.
∵∠OCP=∠ECA,
∴△POC∽△AEC.
4. 如图,在边长为6的正方形ABCD中,Q在CD的延长线上,H在CB的延长线上,∠HCQ绕点C逆时针旋转∠HCH′<45°,得到∠H′CQ′,交AB于点E,交AD的延长线于点N,交BD于点F,NE与BD的交点为M,连接CM. 当BE = 2时.
(1)求ND的长;
(2)求证:CF·EF = MF·BF;
(3)求CM的长.
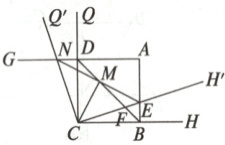
(1)求ND的长;
(2)求证:CF·EF = MF·BF;
(3)求CM的长.

答案:
(1)解:
∵四边形ABCD是正方形,
∴∠ABC=∠CDG=90°,BC=CD,
∵∠HCQ绕点C逆时针旋转∠HCH'<45°,得到H'CQy,
∴∠BCE=∠DCN,
∴△BCE≌△DCN(ASA),
∴DN=BE=2.
(2)证明:
∵四边形ABCD是正方形,
∴∠QCH=∠DCB=90°,∠CBD=∠ABD=45°,
由
(1)△BCE≌DCN,得CE=CN.
由旋转,得∠NCE=∠QCH=90°,
∴△CNE是等腰直角三角形,
∴∠CEN=45°,
∴∠CEN=∠CBD.
∵∠CFB=AFE,
∴△BCF∽△EMF,
∴$\frac{CF}{MF}$=$\frac{BF}{EF}$
∴CF.EF=MF.BF.
(3)解:
∵$\frac{CF}{MF}$=$\frac{BF}{EF}$,∠CFM=∠BFE,
∴△CFM△BFE,,, E= E=45°.
∵△CNE是等腰直角三角形,
∴CM=$\frac{1}{2}$NE.
在Rt△ANE中,
∵AN=ND+AD=2+6=8,AE=
AB−BE=6−2=4,
∴由勾股定理,得
NE= $\sqrt{AN²+AE²}$= $\sqrt{8²+4²}$=4$\sqrt{5}$,
∴CM=$\frac{1}{2}$×4√5=2√5.
(1)解:
∵四边形ABCD是正方形,
∴∠ABC=∠CDG=90°,BC=CD,
∵∠HCQ绕点C逆时针旋转∠HCH'<45°,得到H'CQy,
∴∠BCE=∠DCN,
∴△BCE≌△DCN(ASA),
∴DN=BE=2.
(2)证明:
∵四边形ABCD是正方形,
∴∠QCH=∠DCB=90°,∠CBD=∠ABD=45°,
由
(1)△BCE≌DCN,得CE=CN.
由旋转,得∠NCE=∠QCH=90°,
∴△CNE是等腰直角三角形,
∴∠CEN=45°,
∴∠CEN=∠CBD.
∵∠CFB=AFE,
∴△BCF∽△EMF,
∴$\frac{CF}{MF}$=$\frac{BF}{EF}$
∴CF.EF=MF.BF.
(3)解:
∵$\frac{CF}{MF}$=$\frac{BF}{EF}$,∠CFM=∠BFE,
∴△CFM△BFE,,, E= E=45°.
∵△CNE是等腰直角三角形,
∴CM=$\frac{1}{2}$NE.
在Rt△ANE中,
∵AN=ND+AD=2+6=8,AE=
AB−BE=6−2=4,
∴由勾股定理,得
NE= $\sqrt{AN²+AE²}$= $\sqrt{8²+4²}$=4$\sqrt{5}$,
∴CM=$\frac{1}{2}$×4√5=2√5.
查看更多完整答案,请扫码查看


