《2025年正大图书练测考八年级数学下册鲁教版》

1. 在四边形ABCD中，若AD//BC，AD = BC，∠B = 90°，AB = BC，则四边形ABCD的形状是 （ ）
A. 平行四边形
B. 矩形
C. 菱形
D. 正方形

答案： D

2.（绵阳中考）如图是以正方形的边长为直径，在正方形内画半圆得到的图形，则此图形的对称轴有 （ ）

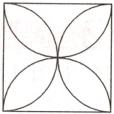
A. 2条
B. 4条
C. 6条
D. 8条

答案： B

3.（2024·淄博高青县期中）正方形具有而菱形不一定具有的性质是 （ ）
A. 四条边都相等
B. 对角线互相垂直且平分
C. 对角线相等
D. 对角线平分一组对角

答案： C

4. 如图，在正方形ABCD中，F是边CD上的一点，AF交对角线BD于点E，连接CE. 若∠EAB = 58°，则∠CEF的度数为 （ ）

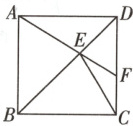
A. 26°
B. 32°
C. 52°
D. 58°

答案： A

5. 如图，把正方形ABCD放在平面直角坐标系中，直角顶点A落在第二象限，顶点B，D分别落在y轴、x轴上，已知点A(-2,2)，B(0,-3)，则点D的坐标为 （ ）

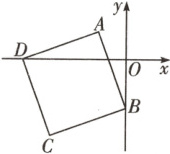
A.（-4,0）
B.（-7,0）
C.（-5,0）
D.（-8,0）

答案： B

6. 如图，E，F分别是正方形ABCD的边CD，BC上的点，且CE = BF，AF，BE相交于点G，下列结论中正确的是 （ ）
①AF = BE； ②AF⊥BE；
③AG = GE； ④$S_{\triangle ABG}=S_{四边形CEGF}$.

A. ①②③
B. ①②④
C. ①③④
D. ②③④

答案： B

7.[教材P23随堂练习T2变式] 如图，在正方形ABCD中，P为对角线AC上一点，∠ABP = 15°，则∠DPC的度数为______.

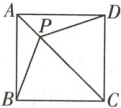
答案： 60°

8. 小明用七巧板拼了一个对角线长为2的正方形，再用这副七巧板拼成一个长方形（如图所示），则长方形的周长为______.

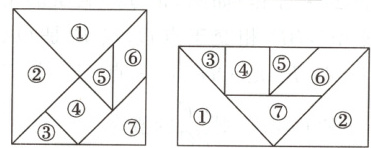
答案： 6

9. 如图，在正方形ABCD中，对角线AC，BD相交于点O，点E，F是对角线AC上的两点，且AE = CF. 连接DE，DF，BE，BF. 求证：四边形DEBF是菱形.

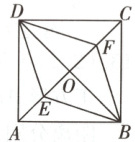
答案： 证明:
∵在正方形ABCD中，对角线AC，BD相交于点O，
∴BD⊥AC,OB=OD,OA=OC.
∵AE=CF,
∴OA−AE=OC−CF,
　即OE=OF,
∴四边形DEBF为平行四边形.
　又
∵BD⊥EF,
∴四边形DEBF是菱形.