第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1. 下列式子中,可能不是二次根式的是( )
A. $\sqrt{3}$
B. $\sqrt{\frac{1}{2}}$
C. $\sqrt{x^{2}-1}$
D. $\sqrt{x^{2}+1}$
A. $\sqrt{3}$
B. $\sqrt{\frac{1}{2}}$
C. $\sqrt{x^{2}-1}$
D. $\sqrt{x^{2}+1}$
答案:
C
2. 下列各式中,正确的是( )
A. $(\sqrt{5})^{2}=5$
B. $-\sqrt{3.6}=-0.6$
C. $\sqrt{(-13)^{2}}=-13$
D. $\sqrt{36}=\pm6$
A. $(\sqrt{5})^{2}=5$
B. $-\sqrt{3.6}=-0.6$
C. $\sqrt{(-13)^{2}}=-13$
D. $\sqrt{36}=\pm6$
答案:
A
3. 式子$\frac{\sqrt{3 - x}}{\sqrt{x - 1}}=\frac{\sqrt{3 - x}}{\sqrt{x - 1}}$成立的条件是( )
A. $x\geq3$
B. $x\leq1$
C. $1\leq x\leq3$
D. $1<x\leq3$
A. $x\geq3$
B. $x\leq1$
C. $1\leq x\leq3$
D. $1<x\leq3$
答案:
D
4. 化简二次根式$-\sqrt{8a^{3}}$的结果为( )
A. $2a\sqrt{2a}$
B. $-2\sqrt{2a^{3}}$
C. $2a\sqrt{-2a}$
D. $-2a\sqrt{2a}$
A. $2a\sqrt{2a}$
B. $-2\sqrt{2a^{3}}$
C. $2a\sqrt{-2a}$
D. $-2a\sqrt{2a}$
答案:
D
5. 已知$a$,$b$分别为等腰三角形的两条边长,且$a$,$b$满足$a = 5\sqrt{b - 6}-4\sqrt{12 - 2b}+3$,则此三角形的周长为________.
答案:
15 解析:由α=5 $\sqrt{b−6}$−4$\sqrt{12−2b}$+3,
得b−6≥0,12−2b≥0,即b≥6,b≤6,
∴b=6,
∴a=5$\sqrt{b−6}$−4$\sqrt{12−2b}$+3=3.
由a,b分别为等腰三角形的两条边长,3+3=6,
可知该等腰三角形是以b=6为腰,a=3为底,
故此三角形的周长为6+6+3=15.
得b−6≥0,12−2b≥0,即b≥6,b≤6,
∴b=6,
∴a=5$\sqrt{b−6}$−4$\sqrt{12−2b}$+3=3.
由a,b分别为等腰三角形的两条边长,3+3=6,
可知该等腰三角形是以b=6为腰,a=3为底,
故此三角形的周长为6+6+3=15.
6. 已知实数$a$,$b$,$c$在数轴上的位置如图所示,且$|a| = |b|$.
$c$ $a$ $0$ $b$
化简:$|a|-b|a + b|+\sqrt{(a - c)^{2}}-\sqrt{c^{2}}$.
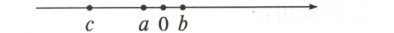
$c$ $a$ $0$ $b$
化简:$|a|-b|a + b|+\sqrt{(a - c)^{2}}-\sqrt{c^{2}}$.
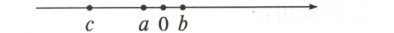
答案:
解:由题意,可得c<a<0<b,,
∴a−c>0.
∵la|=|b|,
∴a+b=0,
∴|a|−bla+b|+ $\sqrt{(a−c)²}$−$\sqrt{c2}$
=−a−0+(a−c)−(−c)
=−a−0+a−c+c
=0.
∴a−c>0.
∵la|=|b|,
∴a+b=0,
∴|a|−bla+b|+ $\sqrt{(a−c)²}$−$\sqrt{c2}$
=−a−0+(a−c)−(−c)
=−a−0+a−c+c
=0.
7. (2024·德州宁津县校级月考)下列各组二次根式中,化简后属于同类二次根式的一组是( )
A. $\sqrt{3}$和$\sqrt{9}$
B. $\sqrt{24}$和$\sqrt{54}$
C. $\sqrt{18}$和$\sqrt{3}$
D. $\sqrt{2\frac{1}{2}}$和$\sqrt{5}$
A. $\sqrt{3}$和$\sqrt{9}$
B. $\sqrt{24}$和$\sqrt{54}$
C. $\sqrt{18}$和$\sqrt{3}$
D. $\sqrt{2\frac{1}{2}}$和$\sqrt{5}$
答案:
B解析:A.$\sqrt{9}$=3,故 $\sqrt{3}$和$\sqrt{9}$不是同类二次根式,故本选项不合题意;
B. $\sqrt{24}$=2√6, $\sqrt{54}$=3$\sqrt{6}$,故$\sqrt{24}$和$\sqrt{54}$是同类二次根式,故本选项符合题意;
C. $\sqrt{18}$=3$\sqrt{2}$,故$\sqrt{18}$与$\sqrt{3}$不是同类二次根式,故本选项不合题意;
D. $\sqrt{\frac{1}{2}}$2 =$\frac{\sqrt{10}}{2}$, $\sqrt{2\frac{1}{2}}$与$\sqrt{5}$不是同类二次根式,故本选项不合题意.
故选B.
B. $\sqrt{24}$=2√6, $\sqrt{54}$=3$\sqrt{6}$,故$\sqrt{24}$和$\sqrt{54}$是同类二次根式,故本选项符合题意;
C. $\sqrt{18}$=3$\sqrt{2}$,故$\sqrt{18}$与$\sqrt{3}$不是同类二次根式,故本选项不合题意;
D. $\sqrt{\frac{1}{2}}$2 =$\frac{\sqrt{10}}{2}$, $\sqrt{2\frac{1}{2}}$与$\sqrt{5}$不是同类二次根式,故本选项不合题意.
故选B.
8. (2024·德州市校级月考)设$\sqrt{2}$的整数部分用$a$表示,小数部分用$b$表示,$4-\sqrt{2}$的整数部分用$c$表示,则$a + b + c$值为( )
A. $2+\sqrt{2}$
B. $2-\sqrt{2}$
C. $2$
D. $1$
A. $2+\sqrt{2}$
B. $2-\sqrt{2}$
C. $2$
D. $1$
答案:
A 解析:
∵1<2<4,
∴1< $\sqrt{2}$<2,
∴a=1,b=√2−1,
2<4−$\sqrt{2}$<3,
∴c=2,
∴a+b+c=1+$\sqrt{2}$−1+2=2+ $\sqrt{2}$
故选A.
∵1<2<4,
∴1< $\sqrt{2}$<2,
∴a=1,b=√2−1,
2<4−$\sqrt{2}$<3,
∴c=2,
∴a+b+c=1+$\sqrt{2}$−1+2=2+ $\sqrt{2}$
故选A.
9. 当$x = \sqrt{13}-1$时,代数式$x^{2}+2x + 2025$的值是________.
答案:
2037
10. 计算:
(1)$3^{0}+|1-\sqrt{3}|-\frac{1}{\sqrt{3}+\sqrt{2}}+\sqrt{18}$;
(2)$(2\sqrt{3}+1)^{2}-(\sqrt{2}+1)(\sqrt{2}-1)$.
(1)$3^{0}+|1-\sqrt{3}|-\frac{1}{\sqrt{3}+\sqrt{2}}+\sqrt{18}$;
(2)$(2\sqrt{3}+1)^{2}-(\sqrt{2}+1)(\sqrt{2}-1)$.
答案:
解:
(1)3°+|1-$\sqrt{3}$|−$\frac{1}{3+\sqrt{2}}$+$\sqrt{18}$
=1+$\sqrt{3}$−1−($\sqrt{3}$$\sqrt{2}$)+3$\sqrt{2}$
=1+$\sqrt{3}$−1| $\sqrt{3}$+$\sqrt{2}$+3$\sqrt{2}$
=4$\sqrt{2}$
(2)(2$\sqrt{3}$+1)²−($\sqrt{2}$+1)($\sqrt{2}$−1)
=12+4$\sqrt{3}$+1−(2−1)
=12+4$\sqrt{3}$+1−1
=12+4$\sqrt{3}$
(1)3°+|1-$\sqrt{3}$|−$\frac{1}{3+\sqrt{2}}$+$\sqrt{18}$
=1+$\sqrt{3}$−1−($\sqrt{3}$$\sqrt{2}$)+3$\sqrt{2}$
=1+$\sqrt{3}$−1| $\sqrt{3}$+$\sqrt{2}$+3$\sqrt{2}$
=4$\sqrt{2}$
(2)(2$\sqrt{3}$+1)²−($\sqrt{2}$+1)($\sqrt{2}$−1)
=12+4$\sqrt{3}$+1−(2−1)
=12+4$\sqrt{3}$+1−1
=12+4$\sqrt{3}$
11. 直角三角形两条直角边长分别为$\sqrt{5}-\sqrt{3}$和$\sqrt{5}+\sqrt{3}$,则该直角三角形斜边上的中线长为( )
A. $\frac{1}{2}$
B. $\sqrt{2}$
C. $1$
D. $2$
A. $\frac{1}{2}$
B. $\sqrt{2}$
C. $1$
D. $2$
答案:
D
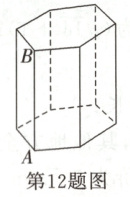
12. (2024·潍坊高密市模拟)如图,直棱柱包装盒子的上、下底面边长都是$6\ cm$的正六边形,侧棱长$8\ cm$,如果用丝线从点$A$处开始经过六个侧面缠绕$n$圈到达点$B$,则丝线长最短需要________$cm$.

答案:
4$\sqrt{4+81n²}$ 解析:如图,将直棱
柱展开,连接AB.
 从点A开始经过6个侧面缠绕
从点A开始经过6个侧面缠绕
n圈到达点B,相当于两条直角边分别是36ncm和8cm,根据两点之间线段最短,可知丝线长最短需要AB的长度.
由勾股定理,得AB= $\sqrt{8²+(36n)²}$=4$\sqrt{4+81n²}$(cm).故丝线长最短需要4$\sqrt{4+81n²}$cm.
4$\sqrt{4+81n²}$ 解析:如图,将直棱
柱展开,连接AB.
 从点A开始经过6个侧面缠绕
从点A开始经过6个侧面缠绕n圈到达点B,相当于两条直角边分别是36ncm和8cm,根据两点之间线段最短,可知丝线长最短需要AB的长度.
由勾股定理,得AB= $\sqrt{8²+(36n)²}$=4$\sqrt{4+81n²}$(cm).故丝线长最短需要4$\sqrt{4+81n²}$cm.
查看更多完整答案,请扫码查看


