《2025年正大图书练测考八年级数学下册鲁教版》

1. 顺次连接四边形ABCD各边中点得到的四边形是菱形，那么AC与BD只需满足（ ）
A. 垂直
B. 相等
C. 互相平分
D. 互相平分且垂直

答案： B

2. 如图，AC，BD是四边形ABCD的对角线，点E，F分别是AD，BC的中点，点M，N分别是AC，BD的中点. 若AB = CD，AB⊥CD，则四边形EMFN是（ ）

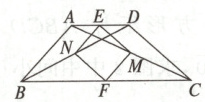
A. 平行四边形
B. 矩形
C. 菱形
D. 正方形

答案： D

3.（2024·泰安岱岳区期中改编）如图，边长为2的菱形ABCD中，∠B = 60°，点E，F分别是BC，CD的中点，则△AEF的周长是（ ）

A. 6
B. 2$\sqrt{3}$
C. 3
D. 3$\sqrt{3}$

答案：
D 解析：
如图，连接AC.
∵四边形ABCD是菱形，∠B = 60°，
∴△ABC是等边三角形.
∵点E是BC的中点，
∴BE = 1，BE⊥AE，
∴AE² + BE² = AB²，
即AE² + 1² = 2²，即AE = √3，且∠EAC = 30°.
同理可得AF = √3，∠FAC = 30°，
∴AE = AF，∠EAC = ∠FAC = 30°，
∴△AEF是等边三角形，
∴△AEF的周长为3×√3 = 3√3.
故选D.

4. 如图，E，F，G，H分别是矩形ABCD各边的中点，AB = 8，BC = 6，则四边形EFGH的面积是________.

答案： 24

5. 如图，在四边形ABCD中，对角线AC，BD相交于点O，点E，F，G，H分别是AB，BC，CD，AD的中点，顺次连接E，F，G，H. 若AC = BD = 4，∠COD = 120°，则四边形EFGH的面积为________.

答案： 2√3

6. 如图，BD，AC是四边形ABCD的对角线，点E，F，G，H分别是线段AD，DB，BC，AC的中点.
（1）求证：线段EG，FH互相平分；
（2）四边形ABCD满足什么条件时，EG⊥FH？证明你得到的结论.

答案：

(1)证明：
如图，连接EF，GF，GH，HE.
∵点E，F分别是线段AD，DB的中点，
∴EF//AB，EF = 1/2AB.
∵点G，H分别是线段BC，AC的中点，
∴GH//AB，GH = 1/2AB，
∴EF//GH，EF = GH，
∴四边形EFGH为平行四边形，
∴线段EG，FH互相平分.
(2)解：当AB = CD时，EG⊥FH，理由如下：
∵点G，F分别是线段BC，BD的中点，
∴GF = 1/2CD.
∵EF = 1/2AB，AB = CD，
∴EF = GF，
∴平行四边形EFGH是菱形，
∴EG⊥FH.