第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
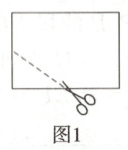
1. 如图,将一个长为20 cm,宽为16 cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图1),再打开,得到如图2所示的小菱形的面积为( )

A. 20 cm²
B. 40 cm²
C. 60 cm²
D. 80 cm²


A. 20 cm²
B. 40 cm²
C. 60 cm²
D. 80 cm²
答案:
B 解析:由题意可得:题图 1 中所得矩形的长为 10 cm,宽为 8 cm,
∵虚线的端点为该矩形两邻边的中点,
∴AC = 8 cm,BD = 10 cm,
∴题图 2 所示的菱形的面积为$\frac{1}{2}×8×10 = 40(cm^{2})$。
故选 B。
∵虚线的端点为该矩形两邻边的中点,
∴AC = 8 cm,BD = 10 cm,
∴题图 2 所示的菱形的面积为$\frac{1}{2}×8×10 = 40(cm^{2})$。
故选 B。
2. 如图,菱形OABC的顶点A在x轴上,CD⊥AB于点D,将菱形沿CD所在直线折叠,点B的对应点为B'。若∠AOC = 45°,点B'的横坐标为4,则点B的坐标为( )
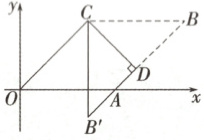
A. (4$\sqrt{2}$+4,4)
B. (8,4)
C. (4$\sqrt{2}$+4,2$\sqrt{2}$)
D. (8,2$\sqrt{2}$)

A. (4$\sqrt{2}$+4,4)
B. (8,4)
C. (4$\sqrt{2}$+4,2$\sqrt{2}$)
D. (8,2$\sqrt{2}$)
答案:
A 解析:如图,令 OA 与 B′C 的交点为 E。
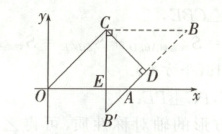
∵四边形 OABC 是菱形,∠AOC = 45°,
∴OC = BC,BC//OA,∠B = ∠AOC = 45°。
∵CD⊥AB,菱形沿 CD 所在直线折叠,点 B 的对应点为 B′,
∴∠B′ = ∠B = 45°,
∴∠BCB′ = 90°,即 BC⊥B′C,
∴OA⊥B′C。
∵点 B′的横坐标为 4,
∴OE = 4。
∵△CEO 是等腰直角三角形,
∴OE = CE = 4,
∴OC = $\sqrt{OE^{2}+CE^{2}}$ = 4$\sqrt{2}$,
∴BC = 4$\sqrt{2}$,
∴点 B 的坐标为(4$\sqrt{2}$ + 4,4)。
故选 A。
A 解析:如图,令 OA 与 B′C 的交点为 E。

∵四边形 OABC 是菱形,∠AOC = 45°,
∴OC = BC,BC//OA,∠B = ∠AOC = 45°。
∵CD⊥AB,菱形沿 CD 所在直线折叠,点 B 的对应点为 B′,
∴∠B′ = ∠B = 45°,
∴∠BCB′ = 90°,即 BC⊥B′C,
∴OA⊥B′C。
∵点 B′的横坐标为 4,
∴OE = 4。
∵△CEO 是等腰直角三角形,
∴OE = CE = 4,
∴OC = $\sqrt{OE^{2}+CE^{2}}$ = 4$\sqrt{2}$,
∴BC = 4$\sqrt{2}$,
∴点 B 的坐标为(4$\sqrt{2}$ + 4,4)。
故选 A。
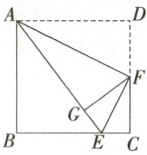
3. (2024·东营期末)如图,在边长为8的正方形纸片ABCD中,E是边BC上的一点,BE = 6,连接AE,将正方形纸片折叠,使点D落在线段AE上的点G处,折痕为AF,则DF的长为________。

答案:
4 解析:
∵四边形 ABCD 是边长为 8 的正方形纸片,BE = 6,
∴AB = BC = CD = DA = 8,∠B = ∠D = ∠C = 90°,
∴AE = $\sqrt{AB^{2}+BE^{2}}$ = 10,CE = BC - BE = 8 - 6 = 2。
由翻折可知 DF = FG,AG = AD = 8,∠AGF = ∠D = 90°,
∴EG = AE - AG = 10 - 8 = 2。
∵FC = DC - DF = 8 - DF,
在 Rt△FGE 和 Rt△FCE 中,FG² + GE² = FC² + EC²,
∴DF² + 2² = (8 - DF)² + 2²,
解得 DF = 4。
∵四边形 ABCD 是边长为 8 的正方形纸片,BE = 6,
∴AB = BC = CD = DA = 8,∠B = ∠D = ∠C = 90°,
∴AE = $\sqrt{AB^{2}+BE^{2}}$ = 10,CE = BC - BE = 8 - 6 = 2。
由翻折可知 DF = FG,AG = AD = 8,∠AGF = ∠D = 90°,
∴EG = AE - AG = 10 - 8 = 2。
∵FC = DC - DF = 8 - DF,
在 Rt△FGE 和 Rt△FCE 中,FG² + GE² = FC² + EC²,
∴DF² + 2² = (8 - DF)² + 2²,
解得 DF = 4。
4. 矩形折叠探究
在矩形纸片ABCD中,AB = 8,BC = 32,点M是边BC上的一点。
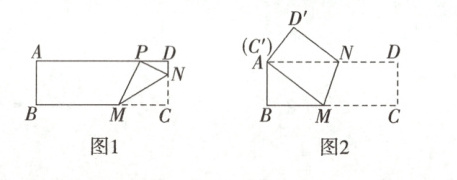
(1)如图1,王欢在边CD上取一点N,将纸片沿直线MN折叠,使点C落在边AD上,记为点P,若DP = 4,求CN的长;
(2)如图2,张乐在边AD上取一点N,将纸片沿直线MN折叠,当点C与点A重合时,求MN的长。
在矩形纸片ABCD中,AB = 8,BC = 32,点M是边BC上的一点。

(1)如图1,王欢在边CD上取一点N,将纸片沿直线MN折叠,使点C落在边AD上,记为点P,若DP = 4,求CN的长;
(2)如图2,张乐在边AD上取一点N,将纸片沿直线MN折叠,当点C与点A重合时,求MN的长。
答案:
解:
(1)
∵四边形 ABCD 是矩形,
∴AB = DC = 8,AD = BC = 32,∠BAD = ∠ABC = ∠BCD = ∠CDA = 90°。
设 CN = x,则 DN = CD - CN = 8 - x,
由折叠可得 PN = CN = x,
在 Rt△PDN 中,DP² + DN² = PN²,
即 4² + (8 - x)² = x²,
解得 x = 5,
即 CN = 5。
(2)当点 C 与点 A 重合时,
设 DN = y,则 AN = AD - DN = 32 - y,
由折叠可得 D′N = DN = y,AD′ = CD = 8,∠AD′N = ∠CDA = 90°。
在 Rt△AD′N 中,AD′² + D′N² = AN²,
即 8² + y² = (32 - y)²,
解得 y = 15,
即 DN = 15。
如图,过点 M 作 MH⊥AD。
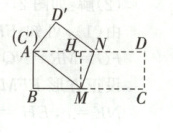
∵四边形 ABCD 是矩形,MH⊥AD,
∴四边形 ABMH,DCMH 是矩形,
则设 HN = a。
∴AH = BM = 32 - 15 - a = 17 - a,HD = MC = AM = 15 + a。
在 Rt△ABM 中,AM² = AB² + MB²,
∴(15 + a)² = 8² + (17 - a)²,
解得 a = 2。
在 Rt△HNM 中,MN² = HM² + HN² = 8² + 2² = 68,
∴MN = $\sqrt{68}$ = 2$\sqrt{17}$。
解:
(1)
∵四边形 ABCD 是矩形,
∴AB = DC = 8,AD = BC = 32,∠BAD = ∠ABC = ∠BCD = ∠CDA = 90°。
设 CN = x,则 DN = CD - CN = 8 - x,
由折叠可得 PN = CN = x,
在 Rt△PDN 中,DP² + DN² = PN²,
即 4² + (8 - x)² = x²,
解得 x = 5,
即 CN = 5。
(2)当点 C 与点 A 重合时,
设 DN = y,则 AN = AD - DN = 32 - y,
由折叠可得 D′N = DN = y,AD′ = CD = 8,∠AD′N = ∠CDA = 90°。
在 Rt△AD′N 中,AD′² + D′N² = AN²,
即 8² + y² = (32 - y)²,
解得 y = 15,
即 DN = 15。
如图,过点 M 作 MH⊥AD。

∵四边形 ABCD 是矩形,MH⊥AD,
∴四边形 ABMH,DCMH 是矩形,
则设 HN = a。
∴AH = BM = 32 - 15 - a = 17 - a,HD = MC = AM = 15 + a。
在 Rt△ABM 中,AM² = AB² + MB²,
∴(15 + a)² = 8² + (17 - a)²,
解得 a = 2。
在 Rt△HNM 中,MN² = HM² + HN² = 8² + 2² = 68,
∴MN = $\sqrt{68}$ = 2$\sqrt{17}$。
5. 如图,以正方形ABCD对角线所在的直线为轴建立平面直角坐标系,其中A(0,1),OD = 1,菱形ABEF的边BE在x轴上,将菱形ABEF绕点O逆时针旋转,每次旋转45°,则第2024次旋转结束时,点F₂₀₂₄的坐标为( )

A. (-1,$\sqrt{2}$)
B. ($\sqrt{2}$,1)
C. (-$\sqrt{2}$,-1)
D. (-$\sqrt{2}$,1)

A. (-1,$\sqrt{2}$)
B. ($\sqrt{2}$,1)
C. (-$\sqrt{2}$,-1)
D. (-$\sqrt{2}$,1)
答案:
B
6. [教材P27习题6.8T4变式]如图,有两个边长为4 cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )

A. 无法确定
B. 8 cm²
C. 16 cm²
D. 4 cm²

A. 无法确定
B. 8 cm²
C. 16 cm²
D. 4 cm²
答案:
D 解析:如图,
∵四边形 ABCD 为正方形,
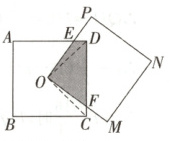
∴OD = OC,∠ODA = ∠OCD = 45°,∠DOC = 90°,
而∠POM = 90°,
即∠DOF + ∠COF = 90°,∠DOE + ∠DOF = 90°,
∴∠DOE = ∠COF。
在△ODE 和△OCF 中,
$\begin{cases}\angle DOE = \angle COF \\OD = OC \\\angle ODE = \angle OCF\end{cases}$
∴△ODE≌△OCF(ASA),
∴$S_{\triangle ODE}$ = $S_{\triangle OCF}$,
∴$S_{四边形 EOFD}$ = $S_{\triangle DOC}$ = $\frac{1}{4}S_{正方形 ABCD}$ = $\frac{1}{4}×4^{2}$ = 4(cm²)。
故选 D。
D 解析:如图,
∵四边形 ABCD 为正方形,

∴OD = OC,∠ODA = ∠OCD = 45°,∠DOC = 90°,
而∠POM = 90°,
即∠DOF + ∠COF = 90°,∠DOE + ∠DOF = 90°,
∴∠DOE = ∠COF。
在△ODE 和△OCF 中,
$\begin{cases}\angle DOE = \angle COF \\OD = OC \\\angle ODE = \angle OCF\end{cases}$
∴△ODE≌△OCF(ASA),
∴$S_{\triangle ODE}$ = $S_{\triangle OCF}$,
∴$S_{四边形 EOFD}$ = $S_{\triangle DOC}$ = $\frac{1}{4}S_{正方形 ABCD}$ = $\frac{1}{4}×4^{2}$ = 4(cm²)。
故选 D。
查看更多完整答案,请扫码查看


