第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1.情境题·数学文化 (2024广西中考)《九章算术》是我国古代重要的数学著作,其中记载了一个问题,大致意思为:现有田出租,第一年3亩1钱,第二年4亩1钱,第三年5亩1钱.三年共得100钱.问:出租的田有多少亩? 设出租的田有x亩,可列方程为 ( )
A.$\frac{x}{3}+\frac{x}{4}+\frac{x}{5}=1$
B.$\frac{x}{3}+\frac{x}{4}+\frac{x}{5}=100$
C.$3x + 4x + 5x = 1$
D.$3x + 4x + 5x = 100$
A.$\frac{x}{3}+\frac{x}{4}+\frac{x}{5}=1$
B.$\frac{x}{3}+\frac{x}{4}+\frac{x}{5}=100$
C.$3x + 4x + 5x = 1$
D.$3x + 4x + 5x = 100$
答案:
根据题意得$\frac{x}{3}×1+\frac{x}{4}×1+\frac{x}{5}×1 = 100$,整理得$\frac{x}{3}+\frac{x}{4}+\frac{x}{5}=100$。故选B。
2.(2024贵州中考)小红学习了等式的性质后,在甲、乙两台天平的左右两边分别放入“■”“●”“▲”三种物体,如图所示,天平都保持平衡.
若设“■”与“●”的质量分别为x,y,则下列关系式正确的是 ( )
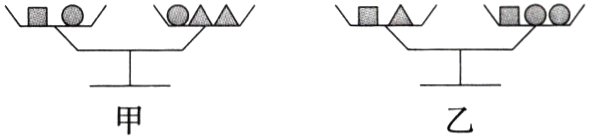
A.$x = y$
B.$x = 2y$
C.$x = 4y$
D.$x = 5y$
若设“■”与“●”的质量分别为x,y,则下列关系式正确的是 ( )

A.$x = y$
B.$x = 2y$
C.$x = 4y$
D.$x = 5y$
答案:
设“△”的质量为z。根据甲天平,得$x + y = y + 2z$①,根据乙天平,得$x + z = x + 2y$②。根据等式的基本性质1,将①的两边同时减y,得$x = 2z$③,根据等式的基本性质1,将②的两边同时减x,得$z = 2y$④,根据等式的基本性质2,将④的两边同时乘2,得$2z = 4y$,
∴$x = 4y$。故选C。
∴$x = 4y$。故选C。
3.(2024山东泰安中考)我国古代《四元玉鉴》中记载“二果问价”问题,其内容大致如下:用九百九十九文钱,可买甜果苦果共一千个,若……,试问买甜果苦果各几个?
设买甜果x个,买苦果y个,可列出符合题意的二元一次方程组$\begin{cases}x + y = 1000,\\\frac{11}{9}x+\frac{4}{7}y = 999,\end{cases}$根据已有信息,题中用“……”表示的缺失的条件应为 ( )
A.甜果七个用四文钱,苦果九个用十一文钱
B.甜果十一个用九文钱,苦果四个用七文钱
C.甜果四个用七文钱,苦果十一个用九文钱
D.甜果九个用十一文钱,苦果七个用四文钱
设买甜果x个,买苦果y个,可列出符合题意的二元一次方程组$\begin{cases}x + y = 1000,\\\frac{11}{9}x+\frac{4}{7}y = 999,\end{cases}$根据已有信息,题中用“……”表示的缺失的条件应为 ( )
A.甜果七个用四文钱,苦果九个用十一文钱
B.甜果十一个用九文钱,苦果四个用七文钱
C.甜果四个用七文钱,苦果十一个用九文钱
D.甜果九个用十一文钱,苦果七个用四文钱
答案:
根据列出的二元一次方程组,可得缺失的条件应为甜果九个用十一文钱,苦果七个用四文钱。故选D。
4.(2024黑龙江齐齐哈尔中考)校团委开展以“我爱读书”为主题的演讲比赛活动,为奖励表现突出的学生,计划拿出200元钱全部用于购买单价分别为8元和10元的两种笔记本(两种都要购买)作为奖品,则购买方案有 ( )
A.5种
B.4种
C.3种
D.2种
A.5种
B.4种
C.3种
D.2种
答案:
设购买8元的笔记本x本,10元的笔记本y本,依题意得$8x + 10y = 200$,整理得$y = 20 - \frac{4}{5}x$,
∵x、y均为正整数,
∴ $\begin{cases}x = 5 \\ y = 16\end{cases}$或$\begin{cases}x = 10 \\ y = 12\end{cases}$或$\begin{cases}x = 15 \\ y = 8\end{cases}$或$\begin{cases}x = 20 \\ y = 4\end{cases}$,
∴购买方案有4种。故选B。
∵x、y均为正整数,
∴ $\begin{cases}x = 5 \\ y = 16\end{cases}$或$\begin{cases}x = 10 \\ y = 12\end{cases}$或$\begin{cases}x = 15 \\ y = 8\end{cases}$或$\begin{cases}x = 20 \\ y = 4\end{cases}$,
∴购买方案有4种。故选B。
5.情境题·现实生活 (2024湖南长沙中考)为庆祝中国改革开放46周年,某中学举办了一场精彩纷呈的庆祝活动,现场参与者均为在校中学生.其中有一个活动项目是“选数字猜出生年份”,该活动项目主持人要求参与者从1,2,3,4,5,6,7,8,9这九个数字中任取一个数字,先乘10,再加上4.6,将此时的运算结果再乘10,然后加上1978,最后减去参与者的出生年份(注:出生年份是一个四位数,比如2010年对应的四位数是2010),得到最终的运算结果.只要参与者报出最终的运算结果,主持人立马就知道参与者的出生年份.若某位参与者报出的最终的运算结果是915,则这位参与者的出生年份是________.
答案:
答案 2009
解析 设这位参与者的出生年份为x,选取的数字为m,则$(10m + 4.6)×10 + 1978 - x = 915$,
∴ $100m + 46 + 1978 - x = 915$,
∴ $x = 1109 + 100m$,
∵此时中学生的出生时间应该在2000年后,
∴ $m = 9$,
∴ $x = 2009$。
解析 设这位参与者的出生年份为x,选取的数字为m,则$(10m + 4.6)×10 + 1978 - x = 915$,
∴ $100m + 46 + 1978 - x = 915$,
∴ $x = 1109 + 100m$,
∵此时中学生的出生时间应该在2000年后,
∴ $m = 9$,
∴ $x = 2009$。
6.(2024浙江中考)解方程组:$\begin{cases}2x - y = 5,\\4x + 3y = -10.\end{cases}$
答案:
解析 $\begin{cases}2x - y = 5① \\ 4x + 3y = -10②\end{cases}$,
①×3 + ②,得$10x = 5$,解得$x = \frac{1}{2}$,
把$x = \frac{1}{2}$代入①,得$2×\frac{1}{2}-y = 5$,解得$y = -4$,
所以方程组的解是$\begin{cases}x = \frac{1}{2} \\ y = -4\end{cases}$。
①×3 + ②,得$10x = 5$,解得$x = \frac{1}{2}$,
把$x = \frac{1}{2}$代入①,得$2×\frac{1}{2}-y = 5$,解得$y = -4$,
所以方程组的解是$\begin{cases}x = \frac{1}{2} \\ y = -4\end{cases}$。
查看更多完整答案,请扫码查看


