《2025年5年中考3年模拟九年级数学下册人教版》

1.(2024湖南张家界桑植期末)下列函数不是反比例函数的是 ( )
A. $y = 3x^{-1}$
B. $y = -\frac{x}{3}$
C. $xy = 5$
D. $y = \frac{1}{2x}$

答案： B A. $y = 3x^{-1}=\frac{3}{x}$，是反比例函数，故A不合题意；B. $y = -\frac{x}{3}$，是正比例函数，故B符合题意；C. $xy = 5$即$y=\frac{5}{x}$，是反比例函数，故C不合题意；D. $y=\frac{1}{2x}=\frac{\frac{1}{2}}{x}$，是反比例函数，故D不合题意. 故选B.

2.两个变量$x$和$y$具有下列关系,其中$y$与$x$成反比例函数关系的是 ( )
A.互为相反数
B.互为倒数
C.相等
D.绝对值相等

答案： B 选项A，$\because x,y$互为相反数，$\therefore y = -x$，则$y$是$x$的正比例函数；选项B，$\because x,y$互为倒数，$\therefore xy = 1$，即$y=\frac{1}{x}$，则$y$是$x$的反比例函数；选项C，$\because x,y$相等，$\therefore y = x$，则$y$是$x$的正比例函数；选项D，$\because x,y$的绝对值相等，$\therefore |y| = |x|$，显然，$y$与$x$不成反比例函数关系. 故选B.

3.(2023湖南株洲中考)下列哪个点在反比例函数$y=\frac{4}{x}$的图象上? ( )
A. $P_1(1,-4)$
B. $P_2(4,-1)$
C. $P_3(2,4)$
D. $P_4(2\sqrt{2},\sqrt{2})$

答案： D $\because 1\times(-4)=4\times(-1)= -4\neq4$，$\therefore P_1(1,-4)$和$P_2(4,-1)$不在反比例函数$y=\frac{4}{x}$的图象上；$\because 2\times4 = 8\neq4$，$\therefore P_3(2,4)$不在反比例函数$y=\frac{4}{x}$的图象上；$\because 2\sqrt{2}\times\sqrt{2}=4$，$\therefore P_4(2\sqrt{2},\sqrt{2})$在反比例函数$y=\frac{4}{x}$的图象上. 故选D.

4.(2024湖南长沙开福三模)若正比例函数$y = -2x$与反比例函数$y = \frac{k}{x}$的图象交于点$(1,-2)$,则另一个交点坐标为(M9226003) ( )
A. $(2,1)$
B. $(-1,2)$
C. $(-2,-1)$
D. $(-2,1)$

答案： B $\because$正比例函数的图象与反比例函数的图象均关于原点对称，$\therefore$两函数图象的交点关于原点对称，$\because$其中一个交点的坐标是$(1,-2)$，$\therefore$另一个交点的坐标是$(-1,2)$. 故选B.

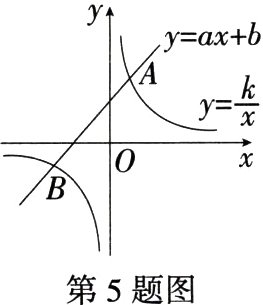
5.(2024辽宁营口一模)如图,一次函数$y = ax + b$与反比例函数$y = \frac{k}{x}$的图象交于点$A(1,2)$,$B(m,-1)$,则$ax + b\geqslant\frac{k}{x}$的解集是 ( )
A. $x ＜ -2$或$0 ＜ x ＜ 1$ B. $x\leqslant -2$或$0 ＜ x\leqslant 1$
C. $-2 ＜ x ＜ 0$或$x ＞ 1$ D. $-2\leqslant x ＜ 0$或$x\geqslant 1$
　　

答案： D $\because A(1,2)$在反比例函数图象上，$\therefore k = 1\times2 = 2$，$\therefore$反比例函数解析式为$y=\frac{2}{x}$，$\because B(m,-1)$在反比例函数图象上，$\therefore -1=\frac{2}{m}$，$\therefore m = -2$，$\therefore B(-2,-1)$，观察图象可知，$ax + b\geqslant\frac{k}{x}$的解集为$-2\leqslant x\lt0$或$x\geqslant1$. 故选D.

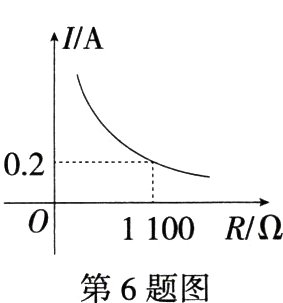
6.(2024山西晋中榆次二模)近几年青少年近视的情况越来越多,为保护视力,某公司推出一款亮度可调节的台灯.我们知道,导体中的电流$I$与导体的电阻$R$、导体两端的电压$U$之间满足关系式$U = IR$,所以台灯灯光亮度的改变,可以通过调节电阻控制电流的变化来实现.如图所示的是该款台灯的电流$I(A)$与电阻$R(\Omega)$成反比例函数关系的图象.根据图象可知,下列说法正确的是(M9226004) ( )
A. $I$与$R$的函数关系式是$I = \frac{1100}{R}(R ＞ 0)$
B.当$R = 500$时,$I = 2$
C.当电阻$R(\Omega)$越大时,该台灯的电流$I(A)$也越大
D.当$500 ＜ R ＜ 880$时,$I$的取值范围是$0.25 ＜ I ＜ 0.44$
　　

答案： D A. $I$与$R$的函数关系式是$I=\frac{220}{R}(R\gt0)$，原说法错误，不符合题意；B. 当$R = 500$时，$I = 0.44$，原说法错误，不符合题意；C. 当电阻$R(\Omega)$越大时，该台灯的电流$I(A)$越小，原说法错误，不符合题意；D. 当$500\lt R\lt880$时，$I$的取值范围是$0.25\lt I\lt0.44$，正确，符合题意. 故选D.

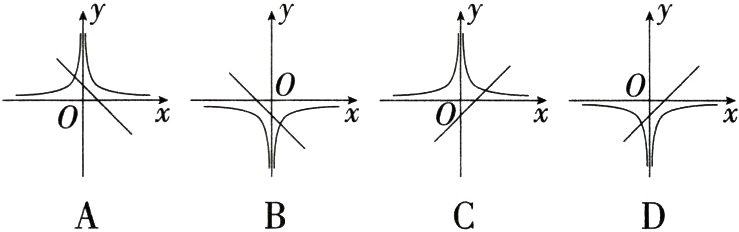
7.(2024黑龙江大庆中考)在同一平面直角坐标系中,函数$y = kx - k(k\neq 0)$与$y = \frac{k}{\vert x\vert}$的图象可能为 ( )
　

答案： C 将$x = 1$代入$y = kx - k$得，$y = k - k = 0$，$\therefore$函数$y = kx - k$的图象过定点$(1,0)$，故选项B不符合；当$k\gt0$时，函数$y = kx - k$的图象经过第一、三、四象限，$y=\frac{k}{|x|}\gt0$，即函数$y=\frac{k}{|x|}$的图象在$x$轴的上方，$\therefore$选项D不符合，C符合；当$k\lt0$时，函数$y = kx - k$的图象经过第一、二、四象限，$y=\frac{k}{|x|}\lt0$，即函数$y=\frac{k}{|x|}$的图象在$x$轴的下方，$\therefore$选项A不符合. 故选C.

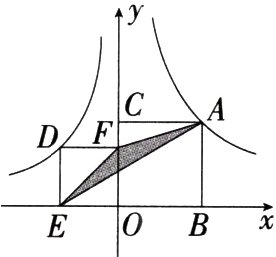
8.(2024甘肃天水秦安三模)如图,反比例函数$y = -\frac{4}{x}$,$y = \frac{6}{x}$的图象分别经过正方形$DEOF$、正方形$ACOB$的顶点$D$、$A$,连接$EF$、$AE$、$AF$,则$\triangle AEF$的面积等于 ( )
A. 2 B. 3 C. 1 D. 5
　　　　　　

答案： A 如图，连接$AO$，$\because$四边形$DEOF$和四边形$ACOB$都是正方形，$\therefore \angle FEO=\angle AOB = 45^{\circ}$，$\therefore EF// AO$，$\therefore S_{\triangle AEF}=S_{\triangle OEF}=\frac{1}{2}\times|-4| = 2$. 故选A.