《2025年5年中考3年模拟九年级数学下册人教版》

11.(2023广东佛山禅城期末)如图，四边形ABCD和四边形EFGH相似，且顶点都在方格纸的格点上，四边形ABCD与四边形EFGH的相似比是 （ ）

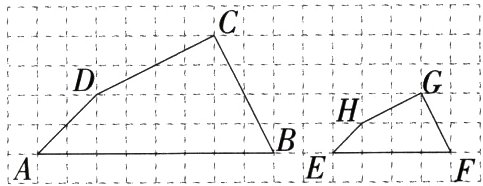
A.1 : 2
B.1 : 4
C.2 : 1
D.4 : 1

答案： 11 C 设方格纸中每个小方格的边长为1，
∵四边形ABCD∽四边形EFGH，
∴相似比$=\frac{AB}{EF}=\frac{8}{4}=2$.故选C.

12.(2023四川成都锦江期末)如图所示的两个四边形相似，则下列结论不正确的是 （ ）

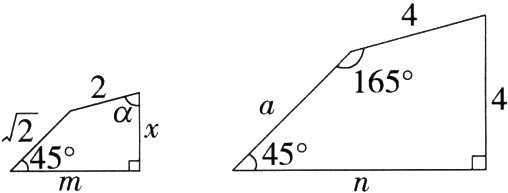
A.a = 2$\sqrt{2}$
B.m = 2n
C.x = 2
D.∠α = 60°

答案： 12 B
∵两个四边形相似，相似比为$2:4 = 1:2$，
∴$\sqrt{2}:a=x:4=m:n = 1:2$，得$a = 2\sqrt{2}$，$x = 2$，$2m = n$，又
∵$\angle\alpha=360^{\circ}-45^{\circ}-90^{\circ}-165^{\circ}=60^{\circ}$，
∴只有选项B结论不正确，符合题意.故选B.

13.(2024辽宁沈阳沈北新区期末)如图，把矩形ABCD对折，折痕为MN，如果矩形DMNC和矩形ABCD相似，那么它们的相似比为 （ ）

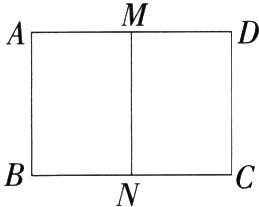
A.$\frac{\sqrt{2}}{2}$
B.$\sqrt{2}$
C.2
D.$\frac{1}{2}$

答案： 13 A 设矩形ABCD的长$AD = x$，宽$AB = y$，则$DM=\frac{1}{2}AD=\frac{1}{2}x$，
∵矩形DMNC与矩形ABCD相似，
∴$\frac{DM}{AB}=\frac{DC}{AD}$，即$\frac{\frac{1}{2}x}{y}=\frac{y}{x}$，即$y^{2}=\frac{1}{2}x^{2}$.
∴$y:x = 1:\sqrt{2}=\frac{\sqrt{2}}{2}$，即矩形DMNC与矩形ABCD的相似比为$\frac{\sqrt{2}}{2}$，故选A.

14.方程思想 (2022湖南衡阳中考,11,★☆☆)在设计人体雕像时，使雕像上部(腰部以上)与下部(腰部以下)的高度比等于下部与全部的高度比，可以增加视觉美感.如图，按此比例设计一座高度为2 m的雷锋雕像，那么该雕像的下部设计高度约是(参考数据:$\sqrt{5}$≈2.236)(M9227001) （ ）

A.0.73 m
B.1.24 m
C.1.37 m
D.1.42 m

答案： 14 B 设下部的高度为$x$ m，则上部的高度是$(2 - x)$ m，
∵雕像上部(腰部以上)与下部(腰部以下)的高度比等于下部与全部的高度比，
∴$\frac{2 - x}{x}=\frac{x}{2}$，解得$x=\sqrt{5}-1$或$x = -\sqrt{5}-1$(舍去)，
∴$x=\sqrt{5}-1\approx1.24$.故选B.

15.设参法 (2021黑龙江大庆中考,12,★☆☆)已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$，则$\frac{x^{2}+xy}{yz}$=________.(M9227001)

答案： 15 答案 $\frac{5}{6}$
解析 设$\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=k(k\neq0)$，则$x = 2k$，$y = 3k$，$z = 4k$，
∴$\frac{x^{2}+xy}{yz}=\frac{4k^{2}+2k\cdot3k}{3k\cdot4k}=\frac{10k^{2}}{12k^{2}}=\frac{5}{6}$.
方法解读
设参法：当题目中出现比例、连等时，设比值等于一个参数(如$k$)，然后把比中的未知数用参数表示，最后在运算时约去参数从而解决问题.

16.(2024河南平顶山郏县期末,13,★☆☆)书画经装裱后更便于收藏.如图，四边形ABCD为长90 cm、宽30 cm的矩形，装裱后整幅画为矩形A'B'C'D'，两矩形的对应边互相平行，且AB与A'B'的距离、CD与C'D'的距离都等于4 cm.当AD与A'D'的距离、BC与B'C'距离都等于a cm，且矩形ABCD∽矩形A'B'C'D'时，整幅书画最美观，此时a的值为________.(M9227002)

答案： 16 答案 12
解析 由题意知$AD = 30$ cm，$AB = 90$ cm，$A'B'=(90 + 2a)$ cm，$A'D' = 30 + 8 = 38$ cm，
∵矩形ABCD∽矩形$A'B'C'D'$，
∴$\frac{A'B'}{AB}=\frac{A'D'}{AD}$，
∴$\frac{90 + 2a}{90}=\frac{38}{30}$，解得$a = 12$.

17.(2024浙江宁波鄞州期末,14,★☆☆)如图，矩形ABCD被分割为3个面积相等的小矩形，已知矩形AFED与原矩形ABCD相似，则原矩形的较长边与较短边的比值是________.(M9227002)

答案： 17 答案 $\sqrt{3}$
解析 设$AF = a$，$AD = b$，
∵矩形ABCD被分割为3个面积相等的小矩形，
∴$NC=\frac{1}{2}b$，$EC = 2a$，
∴$CD = 3a$，
∵矩形AFED与矩形ABCD相似，
∴$\frac{AF}{AD}=\frac{AD}{CD}$，即$\frac{a}{b}=\frac{b}{3a}$，
∴$b=\sqrt{3}a$，
∴原矩形的较长边与较短边的比值为$\frac{3a}{b}=\frac{3a}{\sqrt{3}a}=\sqrt{3}$.

18.推理能力 (2023山东威海中考)四边形ABCD是一张矩形纸片，将其按如图所示的方式折叠，使DA边落在DC边上，点A落在点H处，折痕为DE；使CB边落在CD边上，点B落在点G处，折痕为CF.若矩形HEFG与原矩形ABCD相似，AD = 1，则CD的长为 （ ）

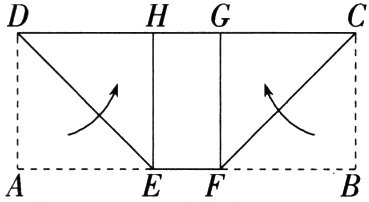
A.$\sqrt{2}-1$
B.$\sqrt{5}-1$
C.$\sqrt{2}+1$
D.$\sqrt{5}+1$

答案： 18 C 设$HG = x$，
∵四边形ABCD是矩形，
∴$\angle A=\angle ADH = 90^{\circ}$，$AD = BC = 1$.由折叠得$GC = BC = 1$，$\angle A=\angle DHE = 90^{\circ}$，$AD = DH = 1$，
∴四边形ADHE是正方形，
∴$AD = HE = 1$.
∵矩形HEFG与原矩形ABCD相似，
∴$\frac{GH}{AD}=\frac{HE}{DC}$，
∴$\frac{x}{1}=\frac{1}{1 + x+1}$，解得$x=\sqrt{2}-1$或$x = -\sqrt{2}-1$(舍去)，
∴$DC = 2 + x=\sqrt{2}+1$.故选C.