《2025年5年中考3年模拟九年级数学下册人教版》

8.(2024江苏南通如皋期末,6,★☆☆)如图,点P在△ABC的边AC上,若只添加一个条件,就可以判定△ABP∽△ACB,下面四种添加条件的方法中,正确的是（M9227004） （ ）

A.$\frac{AB}{AC}=\frac{BP}{BC}$
B.$BP^{2}=AP\cdot PC$
C.$AB^{2}=AP\cdot AC$
D.$BC^{2}=CP\cdot AC$

答案： 8C 当$AB^{2}=AP\cdot AC$时，$\frac{AB}{AC}=\frac{AP}{AB}$，
∵∠A = ∠A，
∴△ABP∽△ACB.故选C.

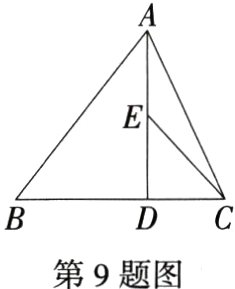
9.(2023海南儋州期末,12,★★☆)如图,在△ABC中,已知AB = 3,AD⊥BC,垂足为D,BD = 2CD.若E是AD的中点,则EC等于（M9227004） （ ）

A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.1
D.$\frac{3}{2}$

答案： 9D
∵$BD = 2CD$，
∴$\frac{CD}{BD}=\frac{1}{2}$，
∵E是AD的中点，
∴$\frac{ED}{AD}=\frac{1}{2}$，
∴$\frac{CD}{BD}=\frac{ED}{AD}$，又
∵$AD\perp BC$，
∴∠ADB = ∠EDC = 90°，
∴△ADB∽△EDC，
∴$\frac{EC}{AB}=\frac{CD}{BD}=\frac{1}{2}$，
∵$AB = 3$，
∴$EC=\frac{3}{2}$.故选D.

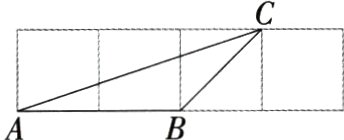
10.(2024江苏盐城东台一模,7,★★☆)如图,在4×1的方格中,每一个小正方形的顶点叫做格点,以其中三个格点为顶点的三角形称为格点三角形.△ABC就是一个格点三角形,现从△ABC的三个顶点所在格点中选取两个,再从余下的格点(除A、B、C外的格点)中选取一个,所能连接成的所有格点三角形中,与△ABC相似的有 （ ）

A.1个
B.2个
C.3个
D.4个

答案：
10C 如图，△ABC∽△CDA，△ABC∽△BCE，△ABC∽△CBF.故选C.
　　　　　　　

11.[情境题·中华优秀传统文化](2024山东济南槐荫期中,13,★★☆)中国象棋是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.如图所示的是中国象棋棋盘的一部分(设各个小正方形的边长均为1),根据“马走日”的规则,“马”落在位置_______(从①②③④中选择合适的序号填写)处,能使“马”“炮”“兵”所在位置的格点连接成的三角形与“帅”“车”“相”所在位置的格点连接成的三角形相似.（M9227004）

答案： 11答案　②
解析　由题图可知“帅”“车”“相”所在位置的格点连接成的三角形的三边长分别为4,2,$2\sqrt{5}$，“兵”“炮”所在位置的格点之间的距离为2，“炮”与②所在位置的格点之间的距离为1，“兵”与②所在位置的格点之间的距离为$\sqrt{5}$，
∵$\frac{4}{2}=\frac{2}{1}=\frac{2\sqrt{5}}{\sqrt{5}}=\frac{2}{1}$，
∴马落在②的位置处时，两个三角形相似.

12.(2024广东茂名茂南期末,20,★★☆)如图,在正方形ABCD中,E、F分别是边AD、CD上的点,且AE = ED,DF = $\frac{1}{4}$DC,连接EF并延长交BC的延长线于点G.（M9227004）
(1)求证:△ABE∽△DEF.
(2)若正方形ABCD的边长为4,求BG的长.

答案： 12解析　
(1)证明：
∵四边形ABCD为正方形，
∴∠A = ∠D = 90°，$AD = AB = DC = BC$，
∵$ED = AE$，
∴$\frac{DE}{AB}=\frac{1}{2}$.
∵$DF=\frac{1}{4}DC$，
∴$\frac{DF}{AE}=\frac{1}{2}$，
∴$\frac{DE}{AB}=\frac{DF}{AE}$，
∴△ABE∽△DEF.
(2)
∵四边形ABCD为正方形，
∴$BG// ED$，
∴△EDF∽△GCF，
∴$\frac{ED}{CG}=\frac{DF}{CF}$.
又
∵$DF=\frac{1}{4}DC$，$AE = ED$，正方形ABCD的边长为4，
∴$\frac{DF}{CF}=\frac{1}{3}$，$ED = 2$，
∴$\frac{2}{CG}=\frac{1}{3}$，
∴$CG = 6$，
∴$BG = BC + CG = 10$.

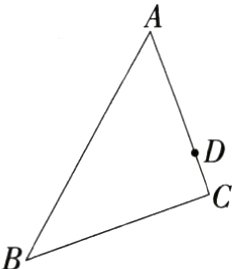
13.[推理能力](2024内蒙古赤峰一模)如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB = 12,AC = 8,AD = 6,当AP的长度为_______时,△ADP和△ABC相似 （ ）

A.9
B.6
C.4或9
D.6或9

答案： 13C 由题意知∠PAD = ∠BAC，则有以下两种情况：
①当$AP:AB = AD:AC$时，△APD∽△ABC，
∴$AP:12 = 6:8$，
∴$AP = 9$；②当$AP:AC = AD:AB$时，△APD∽△ACB，
∴$AP:8 = 6:12$，
∴$AP = 4$.
∴AP的长度为4或9时，△ADP和△ABC相似.故选C.