《2025年5年中考3年模拟九年级数学下册人教版》

1.(2024广西桂林期末)两个相似三角形的相似比是1∶2,则其对应中线之比是 （ ）
A.1∶1
B.1∶2
C.1∶3
D.1∶4

答案： B 两个相似三角形的对应中线之比等于相似比.

2.(2024江西赣州经开区期末)如果两个相似三角形对应边的比为2∶3,那么它们对应高线的比是 (M9227005) （ ）
A.2∶3
B.2∶5
C.4∶9
D.8∶27

答案：
∵两个相似三角形对应边的比为2∶3,
∴两个相似三角形的相似比为2∶3,
∴它们对应高线的比为2∶3.故选A.

3.(2024陕西西安雁塔月考)已知△ABC∽△A₁B₁C₁,AD、A₁D₁分别是△ABC、△A₁B₁C₁的角平分线,BC = 6 cm,B₁C₁ = 4 cm,AD = 4.8 cm,则A₁D₁的长为________cm.

答案： 答案 3.2
解析
∵△ABC∽△A₁B₁C₁,AD、A₁D₁分别是△ABC、△A₁B₁C₁的角平分线,
∴BC∶B₁C₁ = AD∶A₁D₁,
∵BC = 6 cm,B₁C₁ = 4 cm,AD = 4.8 cm,
∴6∶4 = 4.8∶A₁D₁,
∴A₁D₁ = 3.2 cm.

4.(2024辽宁鞍山模拟)如图所示的是伸缩折叠不锈钢晾衣架的侧面示意图,AD与CB相交于点O,AB//CD,根据图中的数据可得x的值为________.(M9227005)

答案：
答案 0.96
解析 如图,过点O作MN⊥AB于点M,MN交CD于点N,则ON = x,OM = 1.2,
∵AB//CD,
∴△OCD∽△OBA,
∴$\frac{ON}{OM}=\frac{CD}{AB}$,即$\frac{x}{1.2}=\frac{0.8}{1}$,
∴x = 0.96.

5.(2024四川内江中考)已知△ABC与△DEF相似,且相似比为1∶3,则△ABC与△DEF的周长之比是 （ ）
A.1∶1
B.1∶3
C.1∶6
D.1∶9

答案： B 两个相似三角形的周长之比等于相似比.

6.(2023重庆中考A卷)若两个相似三角形周长的比为1∶4,则这两个三角形对应边的比是 (M9227005) （ ）
A.1∶2
B.1∶4
C.1∶8
D.1∶16

答案：
∵两个相似三角形周长的比为1∶4,
∴由相似三角形周长的比等于相似比得这两个三角形对应边的比为1∶4.故选B.

7.(2024甘肃张掖甘州模拟)已知△ABC∽△DEF,相似比为3∶1,且△ABC的周长为15,则△DEF的周长为 （ ）
A.1
B.3
C.5
D.45

答案： C
∵△ABC∽△DEF,相似比为3∶1,
∴△ABC的周长与△DEF的周长之比为3∶1,
∵△ABC的周长为15,
∴△DEF的周长为5.故选C.

8.(2024上海宝山期中)已知两个相似三角形的一组对应边长分别是14和9,如果它们的周长相差20,那么较大三角形的周长为________.

答案： 答案 56
解析
∵相似三角形的一组对应边长分别为14和9,
∴其相似比为14∶9,
∵相似三角形的相似比等于对应周长的比,
∴设较大的三角形的周长为14x,则另一三角形的周长为9x,
∴14x - 9x = 20,解得x = 4,所以较大三角形的周长为14x = 14×4 = 56.

9.(2024重庆中考A卷)若两个相似三角形的相似比是1∶3,则这两个相似三角形的面积比是 (M9227005) （ ）
A.1∶3
B.1∶4
C.1∶6
D.1∶9

答案：
∵两个相似三角形的相似比是1∶3,
∴这两个相似三角形的面积比是1²∶3² = 1∶9.故选D.

10.(2021四川雅安中考)如图,将△ABC沿BC边向右平移得到△DEF,DE交AC于点G.若BC∶EC = 3∶1,S△ADG = 16,则S△CEG的值为 （ ）

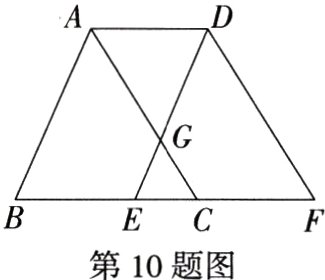
A.2
B.4
C.6
D.8

答案： 由平移的性质可得,AD//BE,AD = BE,
∴△ADG∽△CEG,
∵BC∶EC = 3∶1,
∴BE∶EC = 2∶1,
∴AD∶EC = 2∶1,
∴$\frac{S_{\triangle ADG}}{S_{\triangle CEG}}=(\frac{AD}{EC})^2 = 4$,
∵S_{\triangle ADG}=16,
∴S_{\triangle CEG}=4.故选B.

11.如图,在△ABC中,D、E分别是AB和AC的中点,若S四边形BCED = 15,则S△ABC = (M9227005) （ ）

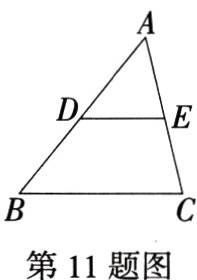
A.30
B.25
C.22.5
D.20

答案：
∵D、E分别是AB和AC的中点,
∴DE是△ABC的中位线,
∴DE//BC,DE=$\frac{1}{2}$BC,
∴△ADE∽△ABC,
∴$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{DE}{BC})^2=\frac{1}{4}$,
∴S_{\triangle ADE}=$\frac{1}{4}$S_{\triangle ABC},
∴S_{四边形BCED}=$\frac{3}{4}$S_{\triangle ABC},
∵S_{四边形BCED}=15,
∴S_{\triangle ABC}=20.故选D.

12.(2024湖南娄底双峰期末)已知△ABC与△A'B'C'相似,相似比为$\frac{2}{3}$,且S△ABC + S△A'B'C' = 91,则△A'B'C'的面积是________.

答案： 答案 63
解析
∵△ABC与△A'B'C'相似,相似比为$\frac{2}{3}$,
∴S_{\triangle ABC}∶S_{\triangle A'B'C'}=4∶9,
∴S_{\triangle ABC}=$\frac{4}{9}$S_{\triangle A'B'C'},
∴S_{\triangle ABC}+S_{\triangle A'B'C'}=$\frac{4}{9}$S_{\triangle A'B'C'}+S_{\triangle A'B'C'}=$\frac{13}{9}$S_{\triangle A'B'C'}=91,
∴S_{\triangle A'B'C'}=63.

13.(2022内蒙古包头中考,9,★☆☆)如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,AC与BD相交于点E,连接AB,CD,则△ABE与△CDE的周长比为(M9227005) （ ）

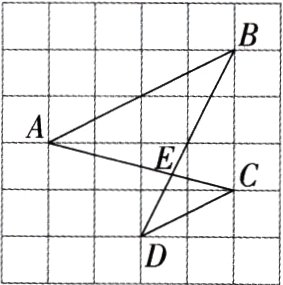
A.1∶4
B.4∶1
C.1∶2
D.2∶1

答案： D 由网格图可知∠BAE = ∠DCA,AB = 2$\sqrt{5}$,CD = $\sqrt{5}$,
∴AB//CD,
∴△ABE∽△CDE,
∴△ABE与△CDE的周长比=$\frac{AB}{CD}$=2.故选D.