第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
7.如图,AD为直角三角形ABC斜边上的高,DE⊥AB于点E,图中相似三角形共有________对.


答案:
答案 10
解析
∵AD是Rt△ABC斜边上的高,DE⊥AB,
∴∠AED=∠ADC=∠BED=∠ADB=∠CAB=90°.
∵∠C=∠C,∠B=∠B,
∴△ACD∽△BCA∽△BDE∽△BAD,
∵∠DAE=∠BAD,
∴△DAE∽△BAD,
∴△ACD∽△BCA∽△BDE∽△BAD∽△DAE,
∴题图中共有10对相似三角形.
解析
∵AD是Rt△ABC斜边上的高,DE⊥AB,
∴∠AED=∠ADC=∠BED=∠ADB=∠CAB=90°.
∵∠C=∠C,∠B=∠B,
∴△ACD∽△BCA∽△BDE∽△BAD,
∵∠DAE=∠BAD,
∴△DAE∽△BAD,
∴△ACD∽△BCA∽△BDE∽△BAD∽△DAE,
∴题图中共有10对相似三角形.
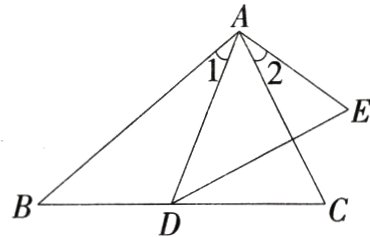
8.(2024广东佛山顺德期末,10,★☆☆)如图,∠1 = ∠2,添加一个条件能判定△ABC∽△ADE的是(M9227004) ( )
①∠C = ∠E;
②∠B = ∠ADE;
③$\frac{AC}{AE}=\frac{BC}{DE}$;
④$\frac{AB}{AD}=\frac{AC}{AE}$.
A.①②③
B.①②④
C.②③④
D.①②③④
①∠C = ∠E;
②∠B = ∠ADE;
③$\frac{AC}{AE}=\frac{BC}{DE}$;
④$\frac{AB}{AD}=\frac{AC}{AE}$.

A.①②③
B.①②④
C.②③④
D.①②③④
答案:
B
∵∠1=∠2,
∴∠DAE=∠BAC.①添加∠C=∠E,可用两角定理判定△ABC∽△ADE,符合题意;②添加∠B=∠ADE,可用两角定理判定△ABC∽△ADE,符合题意;③添加$\frac{AC}{AE}=\frac{BC}{DE}$,无法判定△ABC∽△ADE,不符合题意;④添加$\frac{AB}{AD}=\frac{AC}{AE}$,可用两边夹角定理判定△ABC∽△ADE,符合题意.故选B.
∵∠1=∠2,
∴∠DAE=∠BAC.①添加∠C=∠E,可用两角定理判定△ABC∽△ADE,符合题意;②添加∠B=∠ADE,可用两角定理判定△ABC∽△ADE,符合题意;③添加$\frac{AC}{AE}=\frac{BC}{DE}$,无法判定△ABC∽△ADE,不符合题意;④添加$\frac{AB}{AD}=\frac{AC}{AE}$,可用两边夹角定理判定△ABC∽△ADE,符合题意.故选B.
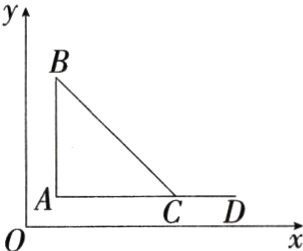
9.(2024陕西西安碑林期末,8,★☆☆)如图,点A,B,C,D的坐标分别是(1,1),(1,5),(5,1),(7,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是(M9227004) ( )
A.(7,-2)
B.(5,-1)
C.(6,0)
D.(7,3)

A.(7,-2)
B.(5,-1)
C.(6,0)
D.(7,3)
答案:
A
∵点A,B,C的坐标分别是(1,1),(1,5),(5,1),
∴AB=AC=4,∠BAC=90°,即△ABC为等腰直角三角形,
∵以C,D,E为顶点的三角形与△ABC相似,
∴△CDE为等腰直角三角形,
∵C,D的坐标分别是(5,1),(7,1),
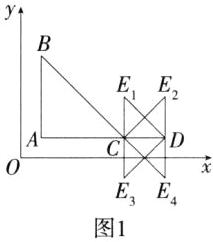
∴CD=2,当CD为腰时,如图1,E₁(5,3)、E₂(7,3)、E₃(5,-1)、E₄(7,-1)符合,当CD为底边时,如图2,E₅(6,2)、E₆(6,0)符合.综上,点E的坐标可能是(5,3),(7,3),(5,-1),(7,-1),(6,2),(6,0).故选A.

A
∵点A,B,C的坐标分别是(1,1),(1,5),(5,1),
∴AB=AC=4,∠BAC=90°,即△ABC为等腰直角三角形,
∵以C,D,E为顶点的三角形与△ABC相似,
∴△CDE为等腰直角三角形,
∵C,D的坐标分别是(5,1),(7,1),
∴CD=2,当CD为腰时,如图1,E₁(5,3)、E₂(7,3)、E₃(5,-1)、E₄(7,-1)符合,当CD为底边时,如图2,E₅(6,2)、E₆(6,0)符合.综上,点E的坐标可能是(5,3),(7,3),(5,-1),(7,-1),(6,2),(6,0).故选A.


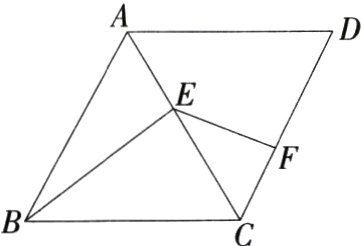
10.(2024广东深圳龙华二模,10,★★☆)如图,在菱形ABCD中,∠ABC = 60°,E是对角线AC上一点,连接BE,作∠BEF = 120°,交CD边于点F,若$\frac{AE}{EC}=\frac{1}{2}$,则$\frac{DF}{FC}$的值为( )
A.$\frac{2\sqrt{3}}{3}$
B.$\frac{\sqrt{10}}{3}$
C.$\frac{4}{3}$
D.$\frac{5}{4}$

A.$\frac{2\sqrt{3}}{3}$
B.$\frac{\sqrt{10}}{3}$
C.$\frac{4}{3}$
D.$\frac{5}{4}$
答案:
D
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠D=∠ABC=60°,
∴△ABC,△ACD是等边三角形,
∴∠BCE=∠ACD=60°,BC=AC,
∴∠CBE+∠BEC=180° - 60° = 120°,
∵∠BEF = 120°,
∴∠CEF +∠BEC=120°,
∴∠CEF=∠CBE,
∵∠ECF=∠BCE,
∴△CEF∽△CBE,
∴CF∶CE=CE∶BC,
∵$\frac{AE}{EC}=\frac{1}{2}$,
∴令AE=x,则EC=2x,
∴AC=x+2x=3x,
∴BC=AC=3x,
∴CF∶2x=2x∶3x,
∴CF=$\frac{4}{3}x$,
∴DF=3x-$\frac{4}{3}x=\frac{5}{3}x$,
∴$\frac{DF}{FC}=\frac{5}{4}$.故选D.
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠D=∠ABC=60°,
∴△ABC,△ACD是等边三角形,
∴∠BCE=∠ACD=60°,BC=AC,
∴∠CBE+∠BEC=180° - 60° = 120°,
∵∠BEF = 120°,
∴∠CEF +∠BEC=120°,
∴∠CEF=∠CBE,
∵∠ECF=∠BCE,
∴△CEF∽△CBE,
∴CF∶CE=CE∶BC,
∵$\frac{AE}{EC}=\frac{1}{2}$,
∴令AE=x,则EC=2x,
∴AC=x+2x=3x,
∴BC=AC=3x,
∴CF∶2x=2x∶3x,
∴CF=$\frac{4}{3}x$,
∴DF=3x-$\frac{4}{3}x=\frac{5}{3}x$,
∴$\frac{DF}{FC}=\frac{5}{4}$.故选D.
11.(2024重庆中考A卷,15,★★☆)如图,在△ABC中,延长AC至点D,使CD = CA,过点D作DE//CB,且DE = DC,连接AE交BC于点F.若∠CAB = ∠CFA,CF = 1,则BF = __________.(M9227004)


答案:
答案 3
解析
∵CD=CA,DE//CB,
∴AF=EF,
∴CF是△ADE的中位线,
∴DE=2CF=2,
∵DE=DC,CD=CA,
∴AC=DE=2,
∵∠CAB=∠CFA,∠ACF=∠ACB,
∴△CAF∽△CBA,
∴AC∶BC=CF∶AC,
∴2∶BC=1∶2,
∴BC=4,
∴BF=BC-FC=3.
解析
∵CD=CA,DE//CB,
∴AF=EF,
∴CF是△ADE的中位线,
∴DE=2CF=2,
∵DE=DC,CD=CA,
∴AC=DE=2,
∵∠CAB=∠CFA,∠ACF=∠ACB,
∴△CAF∽△CBA,
∴AC∶BC=CF∶AC,
∴2∶BC=1∶2,
∴BC=4,
∴BF=BC-FC=3.
12.(2022甘肃武威中考,18,★★☆)如图,在矩形ABCD中,AB = 6 cm,BC = 9 cm,点E,F分别在边AB,BC上,AE = 2 cm,BD,EF交于点G,若G是EF的中点,则BG的长为__________cm.
(M9227004)

(M9227004)

答案:
答案 $\sqrt{13}$
解析
∵四边形ABCD是矩形,
∴CD=AB=6 cm,∠ABC = ∠C = 90°,AB//CD,
∴∠ABD = ∠BDC.
∵AE=2 cm,
∴BE=AB-AE=6-2=4(cm).
∵G是EF的中点,
∴EG = BG=$\frac{1}{2}EF$,
∴∠BEG = ∠ABD,
∴∠BEG=∠BDC,
∴△EBF∽△DCB,
∴$\frac{EB}{DC}=\frac{BF}{CB}$,
∴$\frac{4}{6}=\frac{BF}{9}$,
∴BF = 6 cm,
∴EF = $\sqrt{BE²+BF²}=\sqrt{4²+6²}=2\sqrt{13}$(cm),
∴BG=$\frac{1}{2}EF=\sqrt{13}$(cm).
解析
∵四边形ABCD是矩形,
∴CD=AB=6 cm,∠ABC = ∠C = 90°,AB//CD,
∴∠ABD = ∠BDC.
∵AE=2 cm,
∴BE=AB-AE=6-2=4(cm).
∵G是EF的中点,
∴EG = BG=$\frac{1}{2}EF$,
∴∠BEG = ∠ABD,
∴∠BEG=∠BDC,
∴△EBF∽△DCB,
∴$\frac{EB}{DC}=\frac{BF}{CB}$,
∴$\frac{4}{6}=\frac{BF}{9}$,
∴BF = 6 cm,
∴EF = $\sqrt{BE²+BF²}=\sqrt{4²+6²}=2\sqrt{13}$(cm),
∴BG=$\frac{1}{2}EF=\sqrt{13}$(cm).
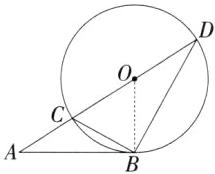
13.(2024广东阳江江城一模,21,★★☆)如图,在△ABD中,O是边AD上的一点,以点O为圆心,OD的长为半径作圆,⊙O恰好与边AB相切于点B,与边AD交于点C,连接BC.
(M9227004)
(1)求证:△ABC∽△ADB.
(2)若AB = 5,AC = 3,求⊙O的半径.

(M9227004)
(1)求证:△ABC∽△ADB.
(2)若AB = 5,AC = 3,求⊙O的半径.

答案:
解析
(1)证明:如图,连接OB,
∵AB与圆O相切于点B,
∴OB⊥AB,
∴∠ABC+∠CBO=90°,
∵CD是圆的直径,
∴∠CBD=90°,
∴∠D+∠OCB=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠D=∠ABC,
∵∠CAB=∠BAD,
∴△ABC∽△ADB.
(2)
∵△ABC∽△ADB,
∴AB∶AD=AC∶AB,
∵AB=5,AC=3,
∴5∶AD=3∶5,
∴AD=$\frac{25}{3}$,
∴CD=AD-AC=$\frac{16}{3}$,
∴☉O的半径是$\frac{1}{2}CD=\frac{8}{3}$.
解析
(1)证明:如图,连接OB,
∵AB与圆O相切于点B,
∴OB⊥AB,
∴∠ABC+∠CBO=90°,
∵CD是圆的直径,
∴∠CBD=90°,
∴∠D+∠OCB=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠D=∠ABC,
∵∠CAB=∠BAD,
∴△ABC∽△ADB.

(2)
∵△ABC∽△ADB,
∴AB∶AD=AC∶AB,
∵AB=5,AC=3,
∴5∶AD=3∶5,
∴AD=$\frac{25}{3}$,
∴CD=AD-AC=$\frac{16}{3}$,
∴☉O的半径是$\frac{1}{2}CD=\frac{8}{3}$.
查看更多完整答案,请扫码查看


