《2025年5年中考3年模拟九年级数学下册人教版》

6.(情境题·数学文化)(2021山东烟台中考)《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示，在井口A处立一根垂直于井口的木杆AB，从木杆的顶端B观察井水水岸D，视线BD与井口的直径AC交于点E，如果测得AB = 1米，AC = 1.6米，AE = 0.4米，那么CD = _______米.(M9227007)
　　　　　　　　　　　　　　

答案： 答案 3
解析
∵AB⊥AC，CD⊥AC，
∴AB//CD，
∴△ABE∽△CDE，
∴$\frac{AB}{CD}=\frac{AE}{CE}$，
∵AC = 1.6米，AE = 0.4米，
∴CE = AC - AE = 1.6 - 0.4 = 1.2(米)，又AB = 1米，
∴$\frac{1}{CD}=\frac{0.4}{1.2}$，
∴CD = 3(米).

7.(2023陕西西安三模)某市为了加快城乡发展，保障市民出行方便，在流经该市的河流上架起一座桥，连通南北，铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥的长.如图，桥AF两侧河岸平行，他们在河岸上选出点B和点C，分别在AB、AC的延长线上取点D、E，使得DE//BC.经测量，BC = 120 m，DE = 210 m，且点E到河岸BC的距离为60 m.已知AF⊥BC，请你根据提供的数据，帮助他们计算桥AF的长度.(M9227007)
　　　　　　　　　　

答案：
解析 如图，过E作EG⊥BC于G，

∵DE//BC，
∴△ABC∽△ADE，
∴$\frac{AC}{AE}=\frac{BC}{DE}=\frac{4}{7}$，
∴$\frac{AC}{EC}=\frac{4}{3}$.
∵AF⊥BC，EG⊥BC，
∴AF//EG，
∴△ACF∽△ECG，
∴$\frac{AF}{EG}=\frac{AC}{EC}$，即$\frac{AF}{60}=\frac{4}{3}$，解得AF = 80(m)，
∴桥AF的长度为80 m.

8.(2024河北邯郸馆陶模拟,12,★★☆)图1所示的是液体沙漏的平面示意图，经过一段时间后的液体如图2所示，此时液面AB =(M9227007)( )
 
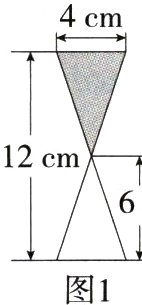
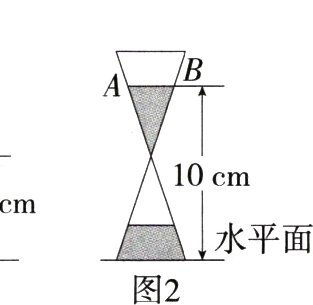
A.$\frac{8}{3}$cm B.3 cm C.$\frac{10}{3}$cm D.4 cm

答案：
A 如图，过O作OM⊥CD，垂足为M，过H作HN⊥AB，垂足为N，由题意可知△CDO∽△ABH，则$\frac{CD}{AB}=\frac{OM}{HN}$，
∵CD = 4 cm，OM = 6 cm，HN = 10 - 6 = 4(cm)，
∴$\frac{4}{AB}=\frac{6}{4}$，
∴AB=$\frac{8}{3}$ cm. 故选A.
　　

9.(2023广东深圳南山三模,7,★★☆)如图，李老师用自制的直角三角形纸板去测“步云阁”的高度，他调整直角三角形纸板的位置，设法使斜边DF保持水平，边DE与点B在同一直线上.已知直角三角形纸板中DE = 18 cm，EF = 12 cm，测得点D离地面的高度为1.8 m，点D到“步云阁”的距离CD为114 m，则“步云阁”的高度AB是(M9227007)( )
　　　　　
A.74.2 m B.77.8 m C.79.6 m D.79.8 m

答案： B 在△DEF和△DCB中，
∵∠D = ∠D，∠DEF = ∠DCB = 90°，
∴△DEF∽△DCB，
∴$\frac{DE}{EF}=\frac{CD}{BC}$，即$\frac{18}{12}=\frac{114}{BC}$，解得BC = 76 m，
∵AC = 1.8 m，
∴AB = AC + BC = 1.8 + 76 = 77.8(m). 故选B.

10.(2024河南南阳西峡期末,8,★★☆)如图，一块材料(△ABC)的形状是锐角三角形，边BC长12 cm，BC边上的高AD为10 cm，把它加工成正方形零件，使正方形的一边GH在BC上，其余两个顶点E、F分别在AB、AC上，则这个正方形零件的边长是(M9227007)( )
　　　　　　　
A.$\frac{60}{11}$cm B.5 cm C.6 cm D.7 cm

答案： A
∵四边形EFHG是正方形，
∴EF//BC，
∴△AEF∽△ABC，又
∵AD⊥BC，
∴$\frac{EF}{BC}=\frac{AK}{AD}$，设正方形零件EFHG的边长为x cm，则AK = (10 - x) cm，
∴$\frac{x}{12}=\frac{10 - x}{10}$，解得x=$\frac{60}{11}$，即这个正方形零件的边长为$\frac{60}{11}$ cm. 故选A.

11.(跨物理·凸透镜成像)(2023河北唐山迁安二模,13,★★☆)凸透镜成像的原理如图所示，O为凸透镜的中心，AD//l//BC，AH⊥l，BD⊥l，CG⊥l，OF₁ = OF₂，若物体到焦点F₁的距离HF₁与焦点F₂到凸透镜中心线DB的距离OF₂之比为3∶2，则该物体缩小为原来的(M9227007)( )
　　　　　
A.$\frac{3}{5}$ B.$\frac{2}{5}$ C.$\frac{2}{3}$ D.$\frac{4}{9}$

答案： C
∵BC//l，CG⊥l，BO⊥l，
∴四边形OBCG为矩形，
∴OB = CG，
∵物体到焦点F₁的距离HF₁与焦点F₂到凸透镜中心线DB的距离OF₂之比为3∶2，
∴$\frac{HF_{1}}{OF_{2}}=\frac{HF_{1}}{OF_{1}}=\frac{3}{2}$，
∵AH⊥HO，BO⊥HO，∠AF₁H = ∠BF₁O，
∴△AHF₁∽△BOF₁，
∴$\frac{AH}{OB}=\frac{HF_{1}}{OF_{1}}=\frac{3}{2}$，
∴$\frac{AH}{CG}=\frac{3}{2}$，
∴$\frac{CG}{AH}=\frac{2}{3}$，即物体缩小为原来的$\frac{2}{3}$. 故选C.