《2025年5年中考3年模拟九年级数学下册人教版》

9.(2023湖南永州中考,9,★☆☆)已知点M(2,a)在反比例函数$y=\frac{k}{x}$的图象上,其中a,k为常数,且k＞0,则点M一定在 ( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： A
∵k ＞ 0，
∴反比例函数y = $\frac{k}{x}$的图象位于第一、三象限，又
∵M(2，a)在该函数图象上，
∴点M一定在第一象限. 故选A.

10.[易错题](2021山西中考,5,★☆☆)已知反比例函数$y=\frac{6}{x}$,则下列描述不正确的是(M9226003) ( )
A.图象位于第一,第三象限
B.图象必经过点$(4,\frac{3}{2})$
C.图象不可能与坐标轴相交
D.y随x的增大而减小

答案： D 选项A，
∵k = 6 ＞ 0，
∴图象位于第一，第三象限，故A描述正确，不符合题意；选项B，
∵4×$\frac{3}{2}$ = 6 = k，
∴图象必经过点(4，$\frac{3}{2}$)，故B描述正确，不符合题意；选项C，
∵x ≠ 0，y ≠ 0，
∴图象不可能与坐标轴相交，故C描述正确，不符合题意；选项D，
∵k = 6 ＞ 0，
∴在每一个象限内，y随x的增大而减小，故D描述错误，符合题意. 故选D.

11.(2024天津中考,8,★☆☆)若点A(x₁,-1),B(x₂,1),C(x₃,5)都在反比例函数$y=\frac{5}{x}$的图象上,则x₁,x₂,x₃的大小关系是 ( )
A.x₁＜x₂＜x₃
B.x₁＜x₃＜x₂
C.x₃＜x₂＜x₁
D.x₂＜x₁＜x₃

答案： B
∵k = 5 ＞ 0，
∴反比例函数y = $\frac{5}{x}$的图象分布在第一、三象限，在每个象限内，y随x的增大而减小.
∵点A(x₁， - 1)，B(x₂，1)，C(x₃，5)都在反比例函数y = $\frac{5}{x}$的图象上，
∴点A(x₁， - 1)位于第三象限，B(x₂，1)，C(x₃，5)位于第一象限，又1 ＜ 5，
∴x₁ ＜ 0，x₂ ＞ x₃ ＞ 0，
∴x₁ ＜ x₃ ＜ x₂. 故选B.

12.(2024北京中考,12,★☆☆)在平面直角坐标系xOy中,若函数$y=\frac{k}{x}(k≠0)$的图象经过点(3,y₁)和(-3,y₂),则y₁+y₂的值是______.

答案： 答案 0
解析
∵函数y = $\frac{k}{x}$(k ≠ 0)的图象经过点(3，y₁)和(- 3，y₂)，
∴y₁ = $\frac{k}{3}$，y₂ = - $\frac{k}{3}$，
∴y₁ + y₂ = 0.

13.[数形结合思想](2024广东梅州兴宁期末,14,★☆☆)一次函数$y=k_1x+b$与反比例函数$y=\frac{k_2}{x}$在同一平面直角坐标系中的图象如图所示,则关于x的不等式$\frac{k_2}{x}＞k_1x+b$的解集为______.

答案： 答案 x ＜ - 2或0 ＜ x ＜ 3
解析 由函数图象看，当x ＜ - 2或0 ＜ x ＜ 3时，双曲线y = $\frac{k_{2}}{x}$在直线y = k₁x + b的上方，故不等式$\frac{k_{2}}{x}$ ＞ k₁x + b的解集为x ＜ - 2或0 ＜ x ＜ 3.

14.(2024江苏南京浦口三模,13,★☆☆)如图,图象①②③分别是反比例函数$y=\frac{a}{x},y=\frac{b}{x},y=\frac{c}{x}(a、b、c为常数)$的部分图象,比较a、b、c的大小:______.(用“＞”连接)(M9226003)

答案： 答案 a ＞ b ＞ c
解析 【解法一】图象③在第四象限，c ＜ 0，图象①②在第三象限，a ＞ 0，b ＞ 0，由图象可知点(- 1， - a)在(- 1， - b)的下方，则 - a ＜ - b，
∴a ＞ b，
∴a ＞ b ＞ c.
【解法二】图象③在第四象限，c ＜ 0，图象①②在第三象限，a ＞ 0，b ＞ 0，
∵相比图象②，图象①离坐标轴更远，
∴a ＞ b，
∴a ＞ b ＞ c.

15.(2024福建福州鼓楼模拟,15,★☆☆)如图所示,点P(3a,a)是反比例函数$y=\frac{k}{x}(k＞0)$的图象与☉O的一个交点,图中阴影部分的面积为10π,则k=______.

答案： 答案 12
解析 因为函数图象关于原点对称，所以阴影部分面积为$\frac{1}{4}$圆的面积，则圆的面积为10π×4 = 40π. 因为P(3a，a)在第一象限，所以a ＞ 0，连接OP，则OP = $\sqrt{(3a)^{2}+a^{2}}$ = $\sqrt{10}a$. 于是π($\sqrt{10}a$)² = 40π，故a = 2(负值已舍去)，所以P点的坐标为(6，2). 将P(6，2)代入y = $\frac{k}{x}$，得k = 6×2 = 12.

16.(2023湖北仙桃模拟,14,★☆☆)已知反比例函数$y=\frac{k}{x}$,当-2≤x≤-1时,y的最大值是4,则当x≥8时,y的最小值为______.(M9226003)

答案： 答案 - $\frac{1}{2}$
解析
∵对于反比例函数y = $\frac{k}{x}$，当 - 2 ≤ x ≤ - 1时，y的最大值是4，
∴函数图象分布在第二、四象限，即k ＜ 0，
∴在每个象限内，y随x的增大而增大，
∴x = - 1时，y取最大值4，
∴4 = $\frac{k}{- 1}$，
∴k = - 4，
∴y = - $\frac{4}{x}$.
∵当x ≥ 8时，y随x的增大而增大，
∴当x = 8时，y取得最小值，此时y = - $\frac{4}{8}$ = - $\frac{1}{2}$.

17.[几何直观](2024湖南岳阳平江二模)如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为$y=\frac{2}{x - 1}$的函数图象.根据这个函数的图象,下列说法正确的是 ( )

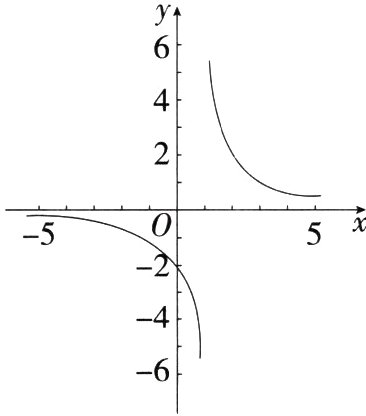
A.图象与x轴没有交点
B.当x＞0时,y＞0
C.函数图象关于原点中心对称
D.y随x的增大而减小

答案： A A中，图象与x轴没有交点，原说法正确；B中，当0 ＜ x ＜ 1时，y ＜ 0，当x ＞ 1时，y ＞ 0，原说法错误；C中，图象关于点(1，0)中心对称，原说法错误；D中，当x ＞ 1时，y随x的增大而减小，当x ＜ 1时，y随x的增大而减小，原说法错误. 故选A.