第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
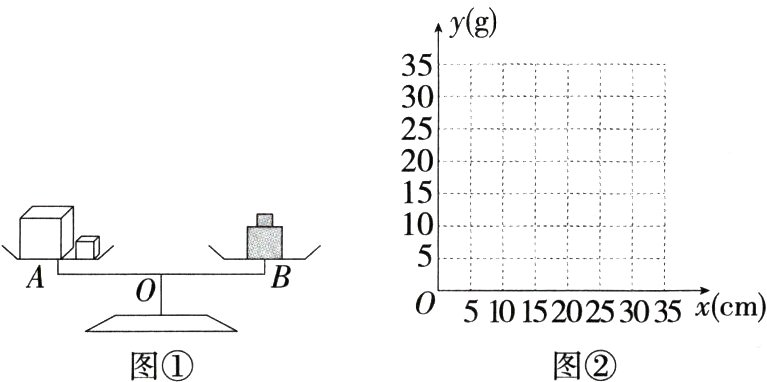
21.[答案含评分细则](12分)(2024江西九江修水二模)如图①,实验课上,小明同学设计了一个探究杠杆平衡条件的实验:在天平的固定托盘A中放置一些大小不等的立方体,在活动托盘B中放置一定质量的砝码,使得天平平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如表:
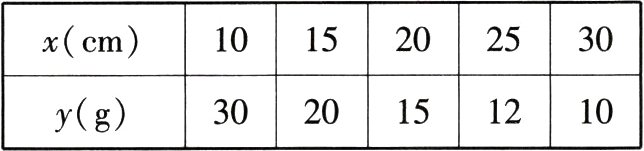
(1)把表中x,y的各组对应值作为点的坐标,如(10,30),(15,20),…在图②的坐标系中描出相应的点,并用平滑的曲线顺次连接这些点.
(2)观察所画的图象,猜测y与x之间的函数关系,求出函数关系式.
(3)当砝码的质量为16 g时,活动托盘B与点O的距离是多少?

(1)把表中x,y的各组对应值作为点的坐标,如(10,30),(15,20),…在图②的坐标系中描出相应的点,并用平滑的曲线顺次连接这些点.
(2)观察所画的图象,猜测y与x之间的函数关系,求出函数关系式.
(3)当砝码的质量为16 g时,活动托盘B与点O的距离是多少?

答案:
21解析 (1)由题意描点、连线,可画出图象如下:
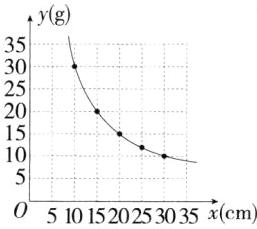
…… 4分
(2)猜测y与x之间的函数关系为反比例函数关系, … 6分
设函数关系式为y = $\frac{k}{x}$(k≠0,x>0),
∵当x = 10时,y = 30,
∴30 = $\frac{k}{10}$,解得k = 300,
∴函数关系式为y = $\frac{300}{x}$(x>0)(经验证,其他点也满足此函数关系式). … 8分
(3)当y = 16时,16 = $\frac{300}{x}$,解得x = $\frac{75}{4}$.
答:活动托盘B与点O的距离是$\frac{75}{4}$ cm. … 12分
21解析 (1)由题意描点、连线,可画出图象如下:

…… 4分
(2)猜测y与x之间的函数关系为反比例函数关系, … 6分
设函数关系式为y = $\frac{k}{x}$(k≠0,x>0),
∵当x = 10时,y = 30,
∴30 = $\frac{k}{10}$,解得k = 300,
∴函数关系式为y = $\frac{300}{x}$(x>0)(经验证,其他点也满足此函数关系式). … 8分
(3)当y = 16时,16 = $\frac{300}{x}$,解得x = $\frac{75}{4}$.
答:活动托盘B与点O的距离是$\frac{75}{4}$ cm. … 12分
22.[答案含评分细则](手拉手模型)(14分)(2022山东烟台中考)【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD = CE.
【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC = ∠ADE = 90°.连接BD,CE.请直接写出$\frac{BD}{CE}$的值.
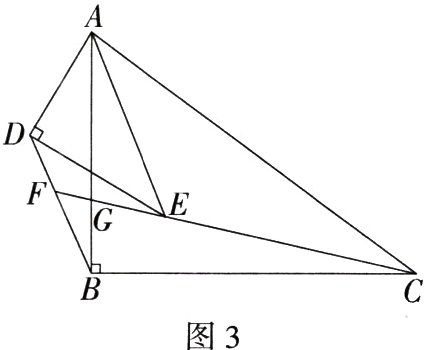
【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC = ∠ADE = 90°,且$\frac{AB}{BC}=\frac{AD}{DE}=\frac{3}{4}$.连接BD,CE.
(1)求$\frac{BD}{CE}$的值.
(2)延长CE交BD于点F,交AB于点G.求sin∠BFC的值.
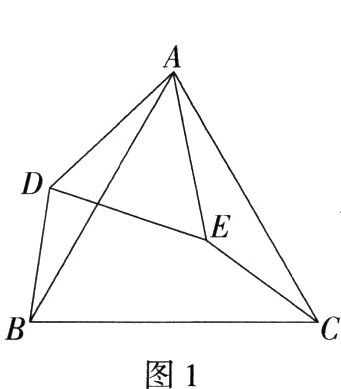
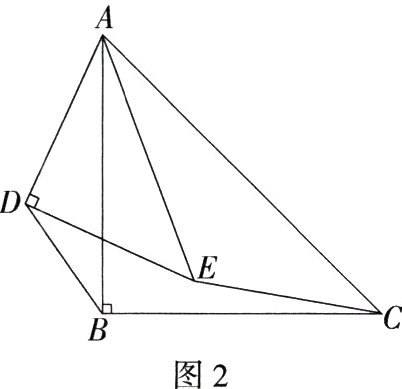
【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC = ∠ADE = 90°.连接BD,CE.请直接写出$\frac{BD}{CE}$的值.
【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC = ∠ADE = 90°,且$\frac{AB}{BC}=\frac{AD}{DE}=\frac{3}{4}$.连接BD,CE.
(1)求$\frac{BD}{CE}$的值.
(2)延长CE交BD于点F,交AB于点G.求sin∠BFC的值.



答案:
22解析 【问题呈现】证明:
∵△ABC和△ADE都是等边三角形,
∴AD = AE,AB = AC,∠DAE = ∠BAC = 60°, … 2分
∴∠DAE - ∠BAE = ∠BAC - ∠BAE,
∴∠BAD = ∠CAE,
∴△BAD≌△CAE(SAS),
∴BD = CE. … 4分
【类比探究】$\frac{BD}{CE}$ = $\frac{\sqrt{2}}{2}$. … 8分
详解:
∵△ABC和△ADE都是等腰直角三角形,
∴$\frac{AD}{AE}$ = $\frac{AB}{AC}$ = $\frac{1}{\sqrt{2}}$,∠DAE = ∠BAC = 45°,
∴∠DAE - ∠BAE = ∠BAC - ∠BAE,
∴∠BAD = ∠CAE,
∴△BAD∽△CAE,
∴$\frac{BD}{CE}$ = $\frac{AB}{AC}$ = $\frac{1}{\sqrt{2}}$ = $\frac{\sqrt{2}}{2}$.
【拓展提升】(1)
∵$\frac{AB}{BC}$ = $\frac{AD}{DE}$ = $\frac{3}{4}$,∠ABC = ∠ADE = 90°,
∴△ABC∽△ADE,
∴∠BAC = ∠DAE,$\frac{AB}{AC}$ = $\frac{AD}{AE}$,
∴∠CAE = ∠BAD,
∴△CAE∽△BAD,
∴$\frac{BD}{CE}$ = $\frac{AB}{AC}$. … 10分
由$\frac{AB}{BC}$ = $\frac{3}{4}$,设AB = 3t,BC = 4t,
则由勾股定理得AC = 5t,
∴$\frac{AB}{AC}$ = $\frac{3}{5}$,
∴$\frac{BD}{CE}$ = $\frac{3}{5}$. … 12分
(2)由(1)得△CAE∽△BAD,
∴∠ACE = ∠ABD,
∵∠AGC = ∠BGF,
∴∠BFC = ∠BAC,
∴sin∠BFC = sin∠BAC = $\frac{BC}{AC}$ = $\frac{4}{5}$. … 14分
∵△ABC和△ADE都是等边三角形,
∴AD = AE,AB = AC,∠DAE = ∠BAC = 60°, … 2分
∴∠DAE - ∠BAE = ∠BAC - ∠BAE,
∴∠BAD = ∠CAE,
∴△BAD≌△CAE(SAS),
∴BD = CE. … 4分
【类比探究】$\frac{BD}{CE}$ = $\frac{\sqrt{2}}{2}$. … 8分
详解:
∵△ABC和△ADE都是等腰直角三角形,
∴$\frac{AD}{AE}$ = $\frac{AB}{AC}$ = $\frac{1}{\sqrt{2}}$,∠DAE = ∠BAC = 45°,
∴∠DAE - ∠BAE = ∠BAC - ∠BAE,
∴∠BAD = ∠CAE,
∴△BAD∽△CAE,
∴$\frac{BD}{CE}$ = $\frac{AB}{AC}$ = $\frac{1}{\sqrt{2}}$ = $\frac{\sqrt{2}}{2}$.
【拓展提升】(1)
∵$\frac{AB}{BC}$ = $\frac{AD}{DE}$ = $\frac{3}{4}$,∠ABC = ∠ADE = 90°,
∴△ABC∽△ADE,
∴∠BAC = ∠DAE,$\frac{AB}{AC}$ = $\frac{AD}{AE}$,
∴∠CAE = ∠BAD,
∴△CAE∽△BAD,
∴$\frac{BD}{CE}$ = $\frac{AB}{AC}$. … 10分
由$\frac{AB}{BC}$ = $\frac{3}{4}$,设AB = 3t,BC = 4t,
则由勾股定理得AC = 5t,
∴$\frac{AB}{AC}$ = $\frac{3}{5}$,
∴$\frac{BD}{CE}$ = $\frac{3}{5}$. … 12分
(2)由(1)得△CAE∽△BAD,
∴∠ACE = ∠ABD,
∵∠AGC = ∠BGF,
∴∠BFC = ∠BAC,
∴sin∠BFC = sin∠BAC = $\frac{BC}{AC}$ = $\frac{4}{5}$. … 14分
查看更多完整答案,请扫码查看


