《2025年5年中考3年模拟九年级数学下册人教版》

1.(2024四川达州渠县月考)在Rt△ABC中,∠ACB =90°,AB =5,BC =4,则cos A的值是(M9228001)
( )
A.$\frac{4}{3}$
B.$\frac{3}{4}$
C.$\frac{4}{5}$
D.$\frac{3}{5}$

答案： 由勾股定理可得$AC = \sqrt{AB^{2}-BC^{2}} = \sqrt{5^{2}-4^{2}} = 3$，$\therefore \cos A=\frac{AC}{AB}=\frac{3}{5}$，故选D.

2.(2024江苏徐州睢宁期末)在Rt△ABC中,∠C = 90°,若sin A=$\frac{2}{3}$,则cos B= ( )
A.$\frac{2}{3}$
B.$\frac{\sqrt{5}}{3}$
C.$\frac{2\sqrt{5}}{5}$
D.$\frac{\sqrt{5}}{2}$

答案： 在Rt△ABC中，∠C = 90°，则$\sin A = \frac{BC}{AB} = \frac{2}{3}$，$\therefore \cos B=\frac{BC}{AB}=\frac{2}{3}$，故选A.

3.(2024甘肃武威凉州一模)在Rt△ABC中,∠C = 90°,cos B = $\frac{5}{7}$,如果AB = 14,那么AC = ________.(M9228001)

答案： 答案 $4\sqrt{6}$。解析 $\because \cos B = \frac{BC}{AB} = \frac{BC}{14} = \frac{5}{7}$，$\therefore BC = 10$，$\therefore AC = \sqrt{AB^{2}-BC^{2}} = \sqrt{14^{2}-10^{2}} = 4\sqrt{6}$。

4.(2024云南中考)如图,在△ABC中,若∠B = 90°, AB = 3,BC = 4,则tan A= ( )
　　　　　　
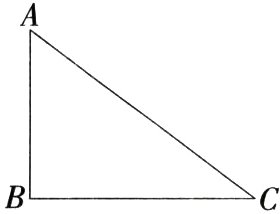
A.$\frac{4}{5}$
B.$\frac{3}{5}$
C.$\frac{4}{3}$
D.$\frac{3}{4}$

答案： $\because$在△ABC中，∠B = 90°，AB = 3，BC = 4，$\therefore \tan A = \frac{BC}{AB} = \frac{4}{3}$，故选C.

5.(2024广东茂名电白期末)在Rt△ABC中,∠C = 90°,BC = 6,AB = 10,则tan B= ( )
A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{4}{5}$
D.$\frac{5}{4}$

答案： $\because \angle C = 90^{\circ}$，BC = 6，AB = 10，$\therefore AC = \sqrt{10^{2}-6^{2}} = 8$，$\therefore \tan B=\frac{AC}{BC}=\frac{8}{6}=\frac{4}{3}$，故选B.

6.设参法(2024云南红河州二模)在Rt△ABC中, ∠C = 90°,AB = 2AC,则∠B的正切值为 ( )
A.1
B.$\frac{1}{2}$
C.$\frac{\sqrt{3}}{3}$
D.$\sqrt{3}$

答案： 由AB = 2AC设AB = 2x，AC = x，$\because \angle C = 90^{\circ}$，$\therefore BC = \sqrt{AB^{2}-AC^{2}} = \sqrt{3}x$，$\therefore \tan B=\frac{AC}{BC}=\frac{x}{\sqrt{3}x}=\frac{\sqrt{3}}{3}$，故选C.

7.教材变式·P65T1(2024陕西渭南富平期末)如图,在Rt△ABC中,∠C = 90°,AB = 8,BC = 4,求cos A和tan A的值.(M9228001)
　　　　　　　　　　　

答案： 解析 $\because \angle C = 90^{\circ}$，AB = 8，BC = 4，$\therefore AC = \sqrt{8^{2}-4^{2}} = 4\sqrt{3}$，$\therefore \cos A=\frac{AC}{AB}=\frac{4\sqrt{3}}{8}=\frac{\sqrt{3}}{2}$，$\tan A=\frac{BC}{AC}=\frac{4}{4\sqrt{3}}=\frac{\sqrt{3}}{3}$.

8.(2024河北张家口张北开学测试)在Rt△ABC中, ∠C = 90°,BC = 2,AB = 3,那么下列各式中,正确的是(M9228001) ( )
A.sin B = $\frac{2}{3}$
B.tan B = $\frac{2}{3}$
C.cos B = $\frac{2}{3}$
D.tan B = $\frac{3}{2}$

答案： 在Rt△ABC中，∠C = 90°，BC = 2，AB = 3，由勾股定理得$AC = \sqrt{AB^{2}-BC^{2}} = \sqrt{3^{2}-2^{2}} = \sqrt{5}$，$\therefore \sin B=\frac{AC}{AB}=\frac{\sqrt{5}}{3}$，$\tan B=\frac{AC}{BC}=\frac{\sqrt{5}}{2}$，$\cos B=\frac{BC}{AB}=\frac{2}{3}$，$\therefore$选项C正确，故选C.

9.(2024江苏常州一模)在Rt△ABC中,∠C = 90°, sin A = $\frac{4}{5}$,则tan A = ________.

答案： 答案 $\frac{4}{3}$。解析 在Rt△ABC中，∠C = 90°，则$\sin A = \frac{BC}{AB} = \frac{4}{5}$，可设BC = 4x，AB = 5x，$\therefore AC = \sqrt{AB^{2}-BC^{2}} = \sqrt{(5x)^{2}-(4x)^{2}} = 3x$，$\therefore \tan A=\frac{BC}{AC}=\frac{4x}{3x}=\frac{4}{3}$.

10.等角转化法(2024甘肃武威 三模,7,)如图,正方形 网格中,点A,O,B,E均在 格点上.☉O过点A,E且 与AB交于点C,点D是☉O上一点,则tan∠CDE = ( )
　　　　　　　　　　　　
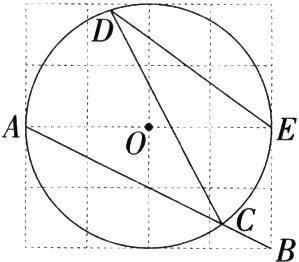
A.$\frac{1}{2}$
B.2
C.$\sqrt{5}$
D.$\frac{\sqrt{5}}{2}$

答案： 设网格中小正方形的边长为1，连接AE、BE(图略)，$\because \angle BAE$与∠CDE都是$\overset{\frown}{CE}$所对的圆周角，$\therefore \angle BAE = \angle CDE$，$\therefore \tan \angle CDE = \tan \angle BAE$. 在Rt△ABE中，$\because \tan \angle BAE=\frac{BE}{AE}=\frac{2}{4}=\frac{1}{2}$，$\therefore \tan \angle CDE=\frac{1}{2}$，故选A.