《2025年5年中考3年模拟九年级数学下册人教版》

1.(2024辽宁阜新新河期末)已知△ABC的三边长分别为1,$\sqrt{2}$,$\sqrt{5}$,△DEF的三边长分别$\sqrt{3}$,$\sqrt{6}$,$\sqrt{15}$,则△ABC与△DEF （ ）
A.一定相似
B.一定不相似
C.不一定相似
D.无法判定是否相似

答案： 1A
∵$\frac{1}{\sqrt{3}}=\frac{\sqrt{2}}{\sqrt{6}}=\frac{\sqrt{5}}{\sqrt{15}}=\frac{\sqrt{3}}{3}$，
∴△ABC与△DEF一定相似.故选A.

2.(2022重庆南岸期末)如图所示,网格中相似的两个三角形是(网格中每个小正方形的边长为1) （ ）

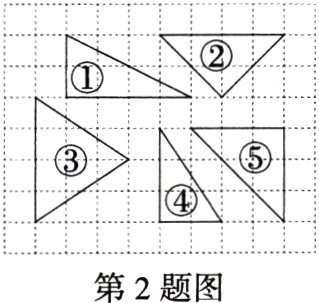
A.①与④
B.②与③
C.①与⑤
D.②与⑤

答案： 2D 由题图知，三角形①的三边长为2,4,$2\sqrt{5}$，三角形②的三边长为$2\sqrt{2}$,$2\sqrt{2}$,4，三角形③的三边长为$\sqrt{13}$,$\sqrt{13}$,4，三角形④的三边长为2,3,$\sqrt{13}$，三角形⑤的三边长为3,3,$3\sqrt{2}$，
∵$\frac{2\sqrt{2}}{3}=\frac{2\sqrt{2}}{3}=\frac{4}{3\sqrt{2}}$，
∴三角形②与三角形⑤相似.

3.如图,已知$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,$\angle BAD = 20^{\circ}$,$\angle DAE = 60^{\circ}$,则∠DAC的度数为_______.

答案： 3答案　40°
解析
∵$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$，
∴△ABC∽△ADE，
∴∠BAC = ∠DAE = 60°，
∵∠BAD = 20°，
∴∠DAC = 60° - 20° = 40°.

4.(2022福建泉州南安模拟)如图,A、B、C三点均在边长为1的小正方形组成的网格的格点上.（M9227004）
(1)请在图中标出点D,连接AD,BD,使得△ABD与△CBA相似.
(2)试证明上述结论.

答案：
4解析　
(1)如图，点D是所求作的点(答案不唯一)，此时△ABD∽△BCA.
　　　　　　　
(2)证明：
∵$AB=\sqrt{1^{2}+2^{2}}=\sqrt{5}$，$BC = 5$，$AC=\sqrt{3^{2}+1^{2}}=\sqrt{10}$，$BD=\sqrt{1^{2}+1^{2}}=\sqrt{2}$，$AD = 1$，
∴$\frac{AD}{AB}=\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$，$\frac{BD}{AC}=\frac{\sqrt{2}}{\sqrt{10}}=\frac{\sqrt{5}}{5}$，$\frac{AB}{BC}=\frac{\sqrt{5}}{5}$，
∴$\frac{AD}{AB}=\frac{BD}{AC}=\frac{AB}{BC}$，
∴△ABD∽△BCA.

5.(2024江苏徐州睢宁模拟)如图,在四边形ABCD中,对角线AC,BD交于点O,若$\frac{OC}{OB}=\frac{OD}{OA}$,则下列说法一定正确的是（M9227004） （ ）

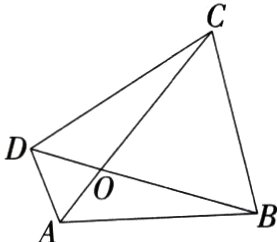
A.△BOA∽△BAD
B.△BOA∽△COD
C.△BOC∽△BCD
D.△COB∽△CBA

答案： 5B
∵$\frac{OC}{OB}=\frac{OD}{OA}$，∠AOB = ∠DOC，
∴△BOA∽△COD.故选B.

6.(2023河北石家庄高邑期末)在三角形纸片ABC中,AB = 9,AC = 6,BC = 12,下列沿虚线剪下的阴影三角形与△ABC相似的是 （ ）

答案： 6B 选项A，
∵公共角为∠B，$\frac{6}{9}\neq\frac{12}{12}$，且$\frac{6}{12}\neq\frac{12}{9}$，
∴阴影三角形与△ABC不相似；选项B，
∵公共角为∠A，$\frac{4}{6}=\frac{6}{9}$，
∴阴影三角形与△ABC相似；选项C，
∵公共角为∠B，$\frac{4}{12}\neq\frac{9}{9}$，且$\frac{4}{9}\neq\frac{9}{12}$，
∴阴影三角形与△ABC不相似；选项D，
∵公共角为∠C，$\frac{4}{12}\neq\frac{6}{6}$，且$\frac{4}{6}\neq\frac{6}{12}$，
∴阴影三角形与△ABC不相似.故选B.

7.[反A字模型](2024广东揭阳期末)如图,在△ABC中,点D、E分别在边AC、AB上,AB = 2AD,AC = 2AE.求证:△ADE∽△ABC.（M9227004）

答案： 7证明
∵$AB = 2AD$，$AC = 2AE$，
∴$\frac{AC}{AE}=\frac{AB}{AD}=2$，
∵∠DAE = ∠BAC，
∴△ADE∽△ABC.