《2025年5年中考3年模拟九年级数学下册人教版》

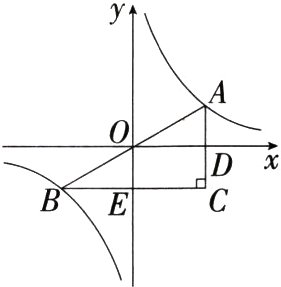
8.(2024福建南平光泽月考)如图,设点A、B是函数$y=\frac{4}{x}$的图象上成中心对称的两个任意点,斜边为AB,两条直角边分别平行于x轴、y轴的直角△ABC的面积为(M9226003) ( )

A.2
B.4
C.8
D.随点A、B的变化而变化

答案： 8C
∵ 点A,B是函数y=$\frac{4}{x}$的图象上成中心对称的两个任意点,直角三角形ABC的两条直角边分别平行于x轴、y轴,
∴ AD = DC,S_{△BOE}=S_{△AOD}=$\frac{|k|}{2}$=2,
∴ S_{矩形ODCE}=2S_{△AOD}=4,
∴ S_{△ABC}=S_{△BOE}+S_{△AOD}+S_{矩形ODCE}=2 + 2 + 4 = 8.故选C.

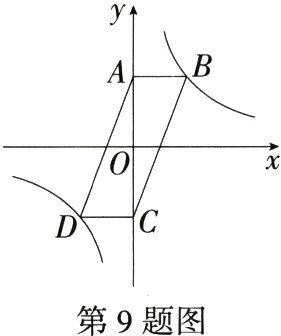
9.(转化与化归思想)(2024广东广州黄埔二模)如图,在□ABCD中,AB//x轴,点B、D在反比例函数$y=\frac{k}{x}(k≠0)$的图象上,若□ABCD的面积是8,则k的值是(M9226003) ( )

A.2
B.4
C.6
D.8

答案：
9B
∵ □ABCD的面积是8,
∴ S_{△ABC}=$\frac{1}{2}$×S_{□ABCD}=$\frac{1}{2}$×8 = 4,由题意可知□ABCD的对称中心为原点O,则OA = OC,连接OB,则S_{△AOB}=$\frac{1}{2}$S_{△ABC}=2,
∴ k=2S_{△AOB}=4.故选B.

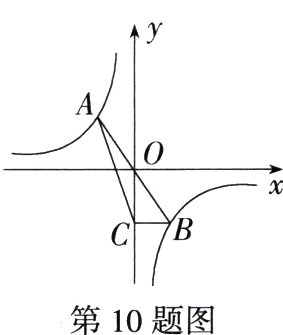
10.(2023安徽马鞍山雨山一模)如图,在平面直角坐标系中,过原点O的直线交反比例函数$y=\frac{k}{x}$的图象于A,B两点,BC⊥y轴于点C,△ABC的面积为6,则k的值为 .(M9226003)

答案： 答案 -6
解析 由对称性可知,OA = OB,
∴ S_{△AOC}=S_{△BOC}=$\frac{1}{2}$S_{△ABC}.
∵ BC⊥y轴,△ABC的面积为6,
∴ S_{△BOC}=$\frac{1}{2}$S_{△ABC}=$\frac{1}{2}$×6=$\frac{1}{2}$|k|,
∵ 反比例函数的图象位于第二、四象限,
∴ k

11.(2024吉林长春双阳一模)如图,点A在反比例函数$y=\frac{12}{x}$的图象上,点B在反比例函数$y=\frac{4}{x}$的图象上,AB//y轴,交x轴于点C,连接OA,取OA的中点D,连接BD,则△ADB(阴影部分)的面积为(M9226003) ( )

A.16
B.8
C.4
D.2

答案：
11D 如图,连接OB,
∵ 点A在反比例函数y=$\frac{12}{x}$的图象上,
∴ S_{△AOC}=$\frac{1}{2}$×12 = 6,
∵ 点B在反比例函数y=$\frac{4}{x}$的图象上,
∴ S_{△BOC}=$\frac{1}{2}$×4 = 2,
∴ S_{△AOB}=S_{△AOC}-S_{△BOC}=6 - 2 = 4,
∵ D是OA的中点,
∴ S_{阴影}=$\frac{1}{2}$S_{△AOB}=$\frac{1}{2}$×4 = 2.故选D.

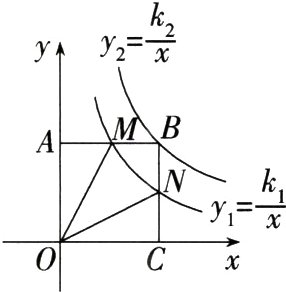
12.(2023湖南长沙岳麓模拟)如图,矩形OABC与反比例函数$y_{1}=\frac{k_{1}}{x}(k_{1}是非零常数,x ＞ 0)$的图象交于点M,N,与反比例函数$y_{2}=\frac{k_{2}}{x}(k_{2}是非零常数,x ＞ 0)$的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则$k_{1}-k_{2}=$ .(M9226003)

答案： 答案 -3
解析
∵ 反比例函数y_{1}=$\frac{k_{1}}{x}$(x＞0)与y_{2}=$\frac{k_{2}}{x}$(x＞0)的图象均在第一象限,
∴ k_{1}＞0,k_{2}＞0.
∵ 点M,N均在反比例函数y_{1}=$\frac{k_{1}}{x}$的图象上,
∴ S_{△OAM}=S_{△OCN}=$\frac{1}{2}$k_{1},
∵ 矩形OABC的顶点B在反比例函数y_{2}=$\frac{k_{2}}{x}$的图象上,
∴ S_{矩形OABC}=k_{2},
∵ S_{四边形OMBN}=S_{矩形OABC}-S_{△OAM}-S_{△OCN}=3,
∴ k_{2}-k_{1}=3,
∴ k_{1}-k_{2}=-3.

13.(2023江苏常州钟楼模拟)如图,平行四边形OABC的顶点O,B在y轴上,顶点A在$y=\frac{k_{1}}{x}(k_{1}＜0)$的图象上,顶点C在$y=\frac{k_{2}}{x}(k_{2}＞0)$的图象上,则平行四边形OABC的面积是 ( )

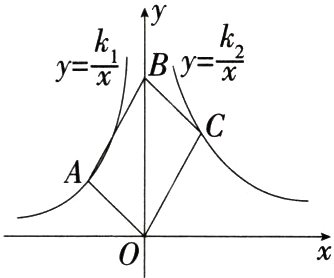
A.-2k₁
B.2k₂
C.k₁ + k₂
D.k₂ - k₁

答案：
13D 如图,过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,根据∠AEB = ∠CDO = 90°,∠ABE = ∠COD,AB = CO得△ABE≌△COD,
∴ △ABE与△COD的面积相等,又
∵ 点C在y=$\frac{k_{2}}{x}$的图象上,
∴ △ABE的面积 = △COD的面积=$\frac{1}{2}$|k_{2}|,同理可得△AOE的面积 = △CBD的面积=$\frac{1}{2}$|k_{1}|,
∴ 平行四边形OABC的面积=2×($\frac{1}{2}$|k_{2}|+$\frac{1}{2}$|k_{1}|)=|k_{2}|+|k_{1}|=k_{2}-k_{1},故选D.

14.(等积变换)(2024陕西西安碑林月考)如图,点A在反比例函数$y=\frac{k}{2x}(x ＞ 0)$的图象上,点B在反比例函数$y=-\frac{k}{x}(x ＜ 0)$的图象上,连接AB,且AB//x轴,点C在x轴上,若$S_{\triangle ABC}=\frac{9}{2}$,则k = .(M9226003)

答案：
答案 6
解析 如图,连接OA,OB,
∵ 点A在反比例函数y=$\frac{k}{2x}$(x＞0)的图象上,点B在反比例函数y=-$\frac{k}{x}$(x0)的图象在第一象限,
∴ k＞0,
∴ k = 6.