《2025年5年中考3年模拟九年级数学下册人教版》

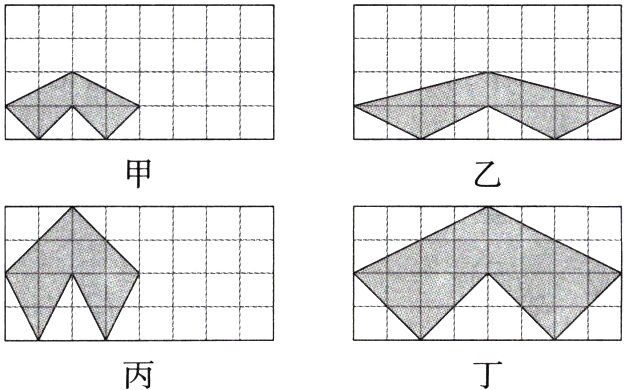
1.(2024江苏连云港中考)下列网格中各个小正方形的边长均为1，阴影部分图形分别记作甲、乙、丙、丁，其中是相似形的为(M9227002)( )
　　　
A.甲和乙
B.乙和丁
C.甲和丙
D.甲和丁

答案： D 观察可知甲和丁形状相同，故甲和丁是相似形，故选D.

2.(2024河南商丘永城期末)下列四条线段中，能与a = 2，b = 3，$c = 3\sqrt{2}$这三条线段组成成比例线段的是(M9227001)( )
$A.d_{1}=1 B.d_{2}=\sqrt{3}$
$C.d_{3}=6 D.d_{4}=\sqrt{2}$

答案： D A项，1×3√2≠2×3，不能组成成比例线段，不符合题意；B项，√3×3√2≠2×3，不能组成成比例线段，不符合题意；C项，2×6≠3×3√2，不能组成成比例线段，不符合题意；D项，√2×3√2 = 2×3，能组成成比例线段，符合题意. 故选D.

3.(2024安徽蚌埠怀远模拟)如图，AD、BC相交于点O，由下列条件不能判定△AOB与△DOC相似的是(M9227004)( )
　　　　　　　
A.AB//CD B.∠A = ∠D
$C.\frac{OA}{OD}=\frac{OB}{OC} D.\frac{OA}{OD}=\frac{AB}{CD}$

答案： D A项，由AB//CD能判定△AOB∽△DOC，不符合题意；B项，由∠AOB = ∠DOC、∠A = ∠D能判定△AOB∽△DOC，不符合题意；C项，由OA/OD = OB/OC、∠AOB = ∠DOC能判定△AOB∽△DOC，不符合题意；D项，已知两边成比例：OA/OD = AB/CD，但由条件得不出相应的夹角相等，不能判定△AOB与△DOC相似，符合题意. 故选D.

4.(2024福建泉州安溪模拟)在△ABC中，点M在边AB上，且$AM=\frac{2}{5}AB，$阅读以下作图步骤：
①以点B为圆心，以适当长为半径画弧，交BA于点D，交BC于点E；
②以点M为圆心，以BD长为半径画弧，交MA于点D'；
③以点D'为圆心，以DE长为半径画弧，交前一条弧于点E'；
④连接ME'并延长，交AC于点N，如图所示.
根据以上作图，一定可以推得的结论是( )
　　　　　　　
$A.\frac{AN}{NC}=\frac{2}{3} B.\frac{AN}{NC}=\frac{2}{5}$
$C.\frac{MN}{BC}=\frac{2}{3} D.\frac{MN}{BC}=\frac{3}{5}$

答案： A
∵AM = 2/5AB，
∴AM/MB = 2/3，由作图可知∠AMN = ∠B，
∴MN//BC，
∴AN/NC = AM/MB = 2/3，△AMN∽△ABC，
∴MN/BC = AM/AB = 2/5，则一定可以推得的结论是A选项中的结论. 故选A.

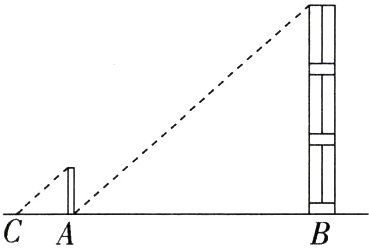
5.(2023四川宜宾叙州期末)数学实践课上，小明在测量教学楼高度时，先测出教学楼落在地面上的影长BA为20米(如图)，然后立刻在A处竖立一根高3米的标杆，测得标杆的影长AC为4米，则楼高为(M9227007)( )
　　　　　　　　　　
A.10米
B.12米
C.15米
D.25米

答案： C
∵标杆的高/标杆的影长 = 楼高/楼影长，即3/4 = 楼高/20，
∴楼高 = 15米. 故选C.

6.(2024四川成都金牛期中)如图，△ABC和△DEF是以点O为位似中心的位似图形.若$BE=\frac{3}{2}OB，$则下列结论正确的是(M9227006)( )
　　　　　　　
$A.\frac{OA}{AD}=\frac{3}{5} B.\frac{OF}{OD}=1$
$C.\frac{AC}{FE}=\frac{2}{5} D.\frac{S_{\triangle ABC}}{S_{\triangle DEF}}=\frac{4}{25}$

答案： D
∵△ABC和△DEF是以点O为位似中心的位似图形，
∴△ABC∽△DEF，AB/DE = OB/OE，
∵BE = 3/2OB，
∴OB/OE = 2/5，则AB/DE = 2/5，
∴S△ABC/S△DEF = (2/5)² = 4/25，故选项D正确. 故选D.