《2025年5年中考3年模拟九年级数学下册人教版》

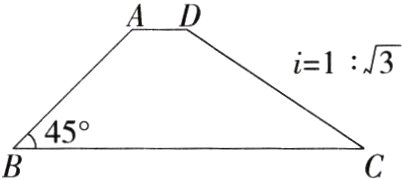
6.(2022湖南邵阳模拟)如图，拦水坝的横断面为梯形ABCD，其中AD//BC，迎水坡AB的坡角∠ABC = 45°，背水坡CD的坡比为1 : $\sqrt{3}$，迎水坡AB的长为8 m，则背水坡CD的长为 （ ）

A.6$\sqrt{2}$ m
B.8$\sqrt{3}$ m
C.4$\sqrt{6}$ m
D.8$\sqrt{2}$ m

答案：
D 如图，过点A作AF⊥BC，垂足为F，过点D作DE⊥BC，垂足为E.
∵AD//BC，
∴AF = DE. 在Rt△ABF中，∠ABF = 45°，AB = 8 m，
∴AF = AB·sin 45° = $8\times\frac{\sqrt{2}}{2}=4\sqrt{2}$(m)，
∴DE = AF = $4\sqrt{2}$ m. 在Rt△DEC中，$\tan\angle DCE=\frac{DE}{CE}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$，
∴∠DCE = 30°，
∴CD = 2DE = $8\sqrt{2}$ m. 故选D.

7.(2022湖南株洲中考)如图1所示，某登山运动爱好者由山坡①的点A处沿线段AC行至山谷点C处，再从点C处沿线段CB行至山坡②的点B处.如图2所示，将直线l视为水平面，山坡①的坡角∠ACM = 30°，AM = 0.6千米，山坡②的坡度i = 1 : 1，BN⊥l于N，且CN = $\sqrt{2}$千米.
(1)求∠ACB的度数.
(2)求在此过程中该登山运动爱好者走过的路程.

答案： 解析
(1)
∵山坡②的坡度i = 1 : 1，
∴CN = BN，
∴∠BCN = 45°，
∴∠ACB = 180° - 30° - 45° = 105°.
(2)在Rt△ACM中，∠AMC = 90°，∠ACM = 30°，AM = 0.6千米，
∴AC = 2AM = 1.2千米，
在Rt△BCN中，∠BNC = 90°，∠BCN = 45°，CN = $\sqrt{2}$千米，
∴BC = $\frac{CN}{\cos\angle BCN}=2$千米，
∴该登山运动爱好者走过的路程为1.2 + 2 = 3.2(千米).
答：该登山运动爱好者走过的路程为3.2千米.

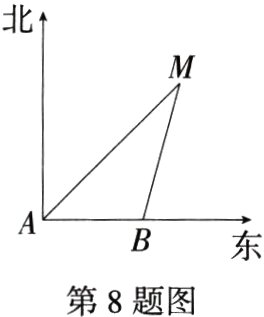
8.(2024河北邯郸模拟，12，★★☆)上午9时，一条船从A处出发，以每小时40海里的速度向正东方向航行，10时到达B处(如图).从A，B两处分别测得小岛M在北偏东45°和北偏东15°方向，那么船在B处时与小岛M的距离为 （ ）

A.20$\sqrt{2}$海里
B.20$\sqrt{3}$海里
C.40海里
D.40$\sqrt{2}$海里

答案：
D 如图，过点B作BN⊥AM于点N，由题意得AB = 40×1 = 40海里，∠ABM = 105°，在Rt△ABN中，BN = AB·sin 45° = $20\sqrt{2}$海里，在Rt△BNM中，∠MBN = 105° - 45° = 60°，
∴∠M = 30°，
∴BM = 2BN = $40\sqrt{2}$海里. 故选D.

9.(2024广东深圳罗湖模拟，9，★★☆)如图，在一次数学实践活动中，小明同学要测量一座与地面垂直的古塔AB的高度，他从古塔底部点B处前行30 m到达斜坡CE的底部点C处，然后沿斜坡CE前行20 m到达最佳测量点D处，在点D处测得塔顶A的仰角为30°，已知斜坡的坡度i = 1 : $\sqrt{3}$，且点A，B，C，D，E在同一平面内，小明同学测得古塔AB的高度是 （ ）

A.(10$\sqrt{3}$ + 20)m
B.(10$\sqrt{3}$ + 10)m
C.20$\sqrt{3}$ m
D.40 m

答案：
A 如图，过点D作DF⊥AB于点F，DG⊥直线BC于点G，由题意得BC = 30 m，CD = 20 m，∠ADF = 30°，DG = BF，DF = BG，
∵斜坡的坡度i = 1 : $\sqrt{3}$，
∴$\frac{DG}{CG}=\frac{1}{\sqrt{3}}$，设DG = x m，则CG = $\sqrt{3}x$ m，
∴CD = 2x m，
∴2x = 20，解得x = 10，
∴DG = BF = 10 m，CG = $10\sqrt{3}$ m，
∴DF = BG = CG + BC = $(30 + 10\sqrt{3})$m，在Rt△ADF中，$\tan 30^{\circ}=\frac{AF}{DF}=\frac{AF}{30 + 10\sqrt{3}}=\frac{\sqrt{3}}{3}$，
∴AF = $(10 + 10\sqrt{3})$m，
∴AB = AF + BF = $(10\sqrt{3}+20)$m. 故选A.

10.(2024四川眉山中考，15，★★☆)如图，斜坡CD的坡度i = 1 : 2，在斜坡上有一棵垂直于水平面的大树AB，当太阳光与水平面的夹角为60°时，大树在斜坡上的影子BE的长为10米，则大树AB的高为__________米.

答案：
答案 $(4\sqrt{15}-2\sqrt{5})$
解析 如图，过点E作CF的平行线，交AB的延长线于点H，则∠BEH = ∠DCF，
∴$\tan\angle BEH=\tan\angle BCF=\frac{BH}{EH}=\frac{1}{2}$，
设BH = x米，则EH = 2x米，
∴BE = $\sqrt{EH^{2}+BH^{2}}=\sqrt{5}x$米，
∴$\sqrt{5}x = 10$，
∴x = $2\sqrt{5}$，
∴BH = $2\sqrt{5}$米，EH = $4\sqrt{5}$米，
∵∠EAH = 180° - 60° - 90° = 30°，
∴AH = $\sqrt{3}EH = 4\sqrt{15}$米，
∴AB = AH - BH = $(4\sqrt{15}-2\sqrt{5})$米，即大树AB的高度为$(4\sqrt{15}-2\sqrt{5})$米.