《2025年5年中考3年模拟九年级数学下册人教版》

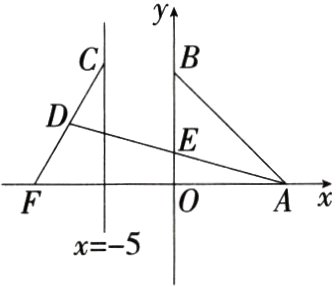
8.新考法(2024江苏南通启东二模)如图，已知A，B两点的坐标分别为(8,0)，(0,8)，点C，F分别是直线x = -5和x轴上的动点，CF = 10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取得最小值时，sin ∠BAD的值是(M9228004)( )

A.$\frac{8}{17}$
B.$\frac{7}{17}$
C.$\frac{4\sqrt{2}}{13}$
D.$\frac{7\sqrt{2}}{26}$

答案：
8D 设直线$x = - 5$交$x$轴于$K$，连接$KD$.由题意，得$KD=\frac{1}{2}CF = 5$，
∴点$D$的运动轨迹是以$K$为圆心，5 为半径的圆，
∴当直线$AD$与$\odot K$相切时，$\triangle ABE$的面积最小，如图，
∵$AD$是切线，点$D$是切点，
∴$AD\perp KD$，
∵$AK = 13$，$DK = 5$，
∴$AD = 12$，
∵$\tan\angle EAO=\frac{OE}{OA}=\frac{DK}{AD}$，
∴$\frac{OE}{8}=\frac{5}{12}$，
∴$OE=\frac{10}{3}$，
∴$AE=\sqrt{OE^{2}+OA^{2}}=\frac{26}{3}$.过$E$作$EH\perp AB$于$H$.
∵$S_{\triangle ABE}=\frac{1}{2}AB\cdot EH = S_{\triangle AOB}-S_{\triangle AOE}$，
∴$EH=\frac{7\sqrt{2}}{3}$，
∴$\sin\angle BAD=\frac{EH}{AE}=\frac{\frac{7\sqrt{2}}{3}}{\frac{26}{3}}=\frac{7\sqrt{2}}{26}$.故选D.

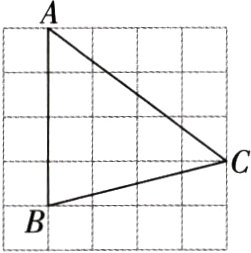
9.如图，在正方形网格中，每个小正方形的边长均是1，△ABC的顶点均在小正方形的顶点上，则sin A的值为________.

答案：
9答案 $\frac{4}{5}$
解析 如图，过点$C$作$CD\perp AB$，垂足为$D$，在$Rt\triangle ADC$中，根据勾股定理得$AC=\sqrt{AD^{2}+CD^{2}}=\sqrt{3^{2}+4^{2}}=5$，
∴$\sin A=\frac{CD}{AC}=\frac{4}{5}$.

10.新独家原创 我们定义：等腰三角形中腰与底边的比叫做顶角的余对(cod).如图，在△ABC中，AB = AC，顶角∠A的余对记作cod A，这时cod A = $\frac{腰}{底边}$ = $\frac{AB}{BC}$.若∠A = 90°，则cod A = ________.(M9228001)

答案： 10答案 $\frac{\sqrt{2}}{2}$
解析 当$\angle A = 90^{\circ}$时，由勾股定理可得$BC=\sqrt{2}AB$，
∴$\cot A=\frac{AB}{BC}=\frac{AB}{\sqrt{2}AB}=\frac{\sqrt{2}}{2}$.

11.(2024广东佛山禅城期中)在△ABC中，∠C = 90°，sin A = $\frac{4}{5}$，AB = 25，则△ABC的周长 = ________.(M9228001)
第二十八章锐角三角函数65

答案： 11答案 60
解析
∵$\angle C = 90^{\circ}$，
∴$\sin A=\frac{BC}{AB}=\frac{4}{5}$，
∴$BC=\frac{4}{5}AB=\frac{4}{5}×25 = 20$，
∴$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{25^{2}-20^{2}}=15$，
∴$\triangle ABC$的周长$=25 + 20+15 = 60$.

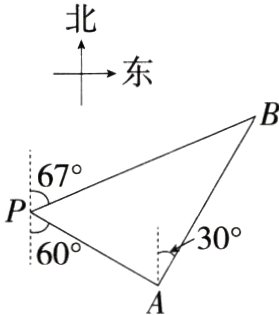
12.(2024湖北武汉模拟)如图，一架无人机位于雷达P的南偏东60°方向，距离雷达35千米的A处，它沿北偏东30°方向航行一段时间后，到达位于雷达P的北偏东67°方向上的B处，此时无人机与雷达P的距离PB约为________千米.(参考数据：sin 37° ≈ 0.60，cos 37° ≈ 0.80，tan 37° ≈ 0.75，结果保留一位小数)(M9228005)

答案：
12答案 58.3
解析 如图，根据题意得$\angle CAP=\angle EPA = 60^{\circ}$，$\angle CAB = 30^{\circ}$，$PA = 35$千米，
∴$\angle PAB = 90^{\circ}$，又$\angle APB = 180^{\circ}-67^{\circ}-60^{\circ}=53^{\circ}$，
∴$\angle B = 180^{\circ}-90^{\circ}-53^{\circ}=37^{\circ}$，在$Rt\triangle PAB$中，$\sin37^{\circ}=\frac{PA}{PB}$，
∴$PB=\frac{PA}{\sin37^{\circ}}=\frac{35}{\sin37^{\circ}}\approx\frac{35}{0.6}\approx58.3$（千米）.

13.(2024内蒙古赤峰中考)综合实践课上，航模小组用无人机测量古树AB的高度.如图，点C处与古树底部A处在同一水平面上，且AC = 10米，无人机从C处竖直上升到达D处，DM为水平线，测得古树顶部B的俯角为45°，古树底部A的俯角为65°，则古树AB的高度约为________米(结果精确到0.1米；参考数据：sin 65° ≈ 0.906，cos 65° ≈ 0.423，tan 65° ≈ 2.145).

答案：
13答案 11.5
解析 由题意，知$DM// AC$，$DC\perp AC$，$\angle MDA = 65^{\circ}$，$\angle MDB = 45^{\circ}$.过点$B$作$BE\perp DC$，垂足为$E$.
∵$BE\perp CD$，$BA\perp AC$，$DC\perp AC$，
∴$\angle C=\angle BEC=\angle CAB = 90^{\circ}$.
∴四边形$CABE$是矩形.
∴$BE = AC = 10$米，$CE = AB$.
∵$DM// AC// BE$，
∴$\angle MDB=\angle EBD = 45^{\circ}$，$\angle MDA=\angle DAC = 65^{\circ}$.在$Rt\triangle ACD$中，
∵$\tan\angle DAC=\frac{DC}{AC}$，
∴$DC=\tan\angle DAC\cdot AC=\tan65^{\circ}×10\approx2.145×10 = 21.45$（米）.在$Rt\triangle DBE$中，
∵$\tan\angle DBE=\frac{DE}{BE}$，
∴$DE=\tan\angle DBE\cdot BE=\tan45^{\circ}×10 = 1×10 = 10$（米）.
∴$AB = DC - DE = 21.45-10 = 11.45\approx11.5$（米）.故答案为 11.5.

14.三垂直模型(2023四川巴中中考)如图，已知正方形ABCD和正方形BEFG，点G在AD上，GF与CD交于点H，tan ∠ABG = $\frac{1}{2}$，正方形ABCD的边长为8，则BH的长为________.(M9228004)

答案： 14答案 10
解析
∵四边形$ABCD$、$BEFG$均为正方形，
∴$\angle A=\angle BGF=\angle D = 90^{\circ}$，
∴$\angle AGB+\angle DGH = 90^{\circ}$，$\angle AGB+\angle ABG = 90^{\circ}$，
∴$\angle DGH=\angle ABG$，
∴$\tan\angle DGH=\tan\angle ABG=\frac{1}{2}$，
∵正方形$ABCD$的边长为 8，
∴$AB = AD = CD = BC = 8$，在$Rt\triangle ABG$中，$AG = AB\cdot\tan\angle ABG = 8×\frac{1}{2}=4$，
∴$DG = AD - AG = 4$，在$Rt\triangle DGH$中，$DH = DG\cdot\tan\angle DGH = 4×\frac{1}{2}=2$，
∴$CH = CD - DH = 8 - 2 = 6$.在$Rt\triangle BCH$中，$BH=\sqrt{CH^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}}=10$.