第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
10.(一线三等角模型)(2024广东中山二模)如图,正方形ABCD的顶点B在x轴上,点A,点C在反比例函数y = $\frac{k}{x}$(k>0,x>0)图象上.若直线BC的函数表达式为y = $\frac{1}{2}$x - 4,则反比例函数表达式为(M9226002) ( )

A.y = $\frac{6}{x}$
B.y = $\frac{12}{x}$
C.y = $\frac{16}{x}$
D.y = $\frac{24}{x}$

A.y = $\frac{6}{x}$
B.y = $\frac{12}{x}$
C.y = $\frac{16}{x}$
D.y = $\frac{24}{x}$
答案:
如图,设直线BC与y轴交于点G,在y = $\frac{1}{2}$x - 4中,令y = 0,则x = 8,令x = 0,则y = -4,
∴B(8,0),G(0,-4),
∴OB = 8,OG = 4,过A作AE⊥x轴于E,过C作CF⊥x轴于F,
∵四边形ABCD是正方形,
∴AB = BC,∠ABC = 90°,
∴∠EAB + ∠ABE = ∠ABE + ∠CBF = 90°,
∴∠EAB = ∠CBF,在△AEB与△BFC中,$\begin{cases}∠AEB = ∠BFC = 90° \\∠BAE = ∠FBC \\AB = BC\end{cases}$,
∴△AEB≌△BFC(AAS),
∴AE = BF,BE = CF,
∵∠BOG = ∠BFC = 90°,∠OBG = ∠CBF,
∴△OBG∽△FBC,
∴$\frac{CF}{BF}$=$\frac{OG}{OB}$=$\frac{1}{2}$,
∴设CF = a,BF = 2a,则AE = 2a,BE = a,
∴A(8 - a,2a),C(8 + 2a,a),
∵点A,点C在反比例函数y = $\frac{k}{x}$(k>0,x>0)图象上,
∴2a(8 - a)=a(8 + 2a),
∴a = 2或a = 0(舍去),
∴A(6,4),
∴k = 4×6 = 24,
∴反比例函数表达式为y = $\frac{24}{x}$.故选D.
如图,设直线BC与y轴交于点G,在y = $\frac{1}{2}$x - 4中,令y = 0,则x = 8,令x = 0,则y = -4,
∴B(8,0),G(0,-4),
∴OB = 8,OG = 4,过A作AE⊥x轴于E,过C作CF⊥x轴于F,
∵四边形ABCD是正方形,
∴AB = BC,∠ABC = 90°,
∴∠EAB + ∠ABE = ∠ABE + ∠CBF = 90°,
∴∠EAB = ∠CBF,在△AEB与△BFC中,$\begin{cases}∠AEB = ∠BFC = 90° \\∠BAE = ∠FBC \\AB = BC\end{cases}$,
∴△AEB≌△BFC(AAS),
∴AE = BF,BE = CF,
∵∠BOG = ∠BFC = 90°,∠OBG = ∠CBF,
∴△OBG∽△FBC,
∴$\frac{CF}{BF}$=$\frac{OG}{OB}$=$\frac{1}{2}$,
∴设CF = a,BF = 2a,则AE = 2a,BE = a,
∴A(8 - a,2a),C(8 + 2a,a),
∵点A,点C在反比例函数y = $\frac{k}{x}$(k>0,x>0)图象上,
∴2a(8 - a)=a(8 + 2a),
∴a = 2或a = 0(舍去),
∴A(6,4),
∴k = 4×6 = 24,
∴反比例函数表达式为y = $\frac{24}{x}$.故选D.

11.(新独家原创)已知函数y = (k² + k)x^{k² - k - 1}是反比例函数,则($\sqrt{2026}$ + k)($\sqrt{2026}$ - k) = ________.
答案:
答案 2025 解析 由题意得k² - k - 1 = -1,且k² + k≠0,解得k = 1,
∴($\sqrt{2026}$+k)($\sqrt{2026}$-k)=($\sqrt{2026}$+1)·($\sqrt{2026}$-1)=2026 - 1 = 2025.
∴($\sqrt{2026}$+k)($\sqrt{2026}$-k)=($\sqrt{2026}$+1)·($\sqrt{2026}$-1)=2026 - 1 = 2025.
12.(新考向·开放型试题)(2024云南昆明五华三模)如图,在△ABC中,点E在AB边上,已知AC//BD,添加一个条件,使△BDE∽△ABC.你添加的条件是________.(M9227004)


答案:
答案 ∠BDE = ∠ABC(或∠BED = ∠ACB或$\frac{BD}{AB}$=$\frac{BE}{AC}$,答案不唯一)解析
∵AC//BD,
∴∠DBE = ∠BAC,则添加∠BDE = ∠ABC或∠BED = ∠ACB,可依据“两角分别相等的两个三角形相似”得出△BDE∽△ABC;添加$\frac{BD}{AB}$=$\frac{BE}{AC}$,可依据“两边成比例且夹角相等的两个三角形相似”得出△BDE∽△ABC.
∵AC//BD,
∴∠DBE = ∠BAC,则添加∠BDE = ∠ABC或∠BED = ∠ACB,可依据“两角分别相等的两个三角形相似”得出△BDE∽△ABC;添加$\frac{BD}{AB}$=$\frac{BE}{AC}$,可依据“两边成比例且夹角相等的两个三角形相似”得出△BDE∽△ABC.
13.(2024山东滨州滨城二模)如图,将△ABC平移到△DEF的位置,点A的对应点为点D,DE、DF分别交BC于点G、H,若AB = 3DG,则$\frac{S_{\triangle DGH}}{S_{\triangle ABC}}$ = ________.(M9227005)
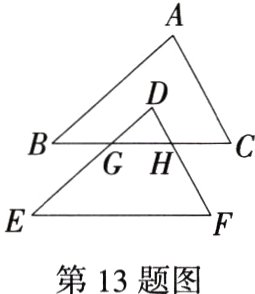

答案:
答案 $\frac{1}{9}$解析 由平移的性质得△ABC≌△DEF,GH//EF,
∴AB = DE,△DGH∽△DEF,
∵AB = 3DG,
∴DE = 3DG,即$\frac{DG}{DE}$=$\frac{1}{3}$,
∵△DGH∽△DEF,
∴$\frac{S_{\triangle DGH}}{S_{\triangle DEF}}$=($\frac{DG}{DE}$)² = ($\frac{1}{3}$)²=$\frac{1}{9}$,
∴$\frac{S_{\triangle DGH}}{S_{\triangle ABC}}$=$\frac{1}{9}$.
∴AB = DE,△DGH∽△DEF,
∵AB = 3DG,
∴DE = 3DG,即$\frac{DG}{DE}$=$\frac{1}{3}$,
∵△DGH∽△DEF,
∴$\frac{S_{\triangle DGH}}{S_{\triangle DEF}}$=($\frac{DG}{DE}$)² = ($\frac{1}{3}$)²=$\frac{1}{9}$,
∴$\frac{S_{\triangle DGH}}{S_{\triangle ABC}}$=$\frac{1}{9}$.
14.(跨物理·电学)(2024江苏盐城盐都二模)图1是一电路图,滑动变阻器的电阻为R,电功率为P,P关于R的反比例函数图象如图2所示.小明通过调节电阻,发现当R从10 Ω增加到20 Ω时,电功率P减少了20 W,则当R = 25 Ω时,P = ________W.(M9227004)




答案:
答案 16 解析 设R为10Ω时,P为x W,根据题意得10x = 20(x - 20),解得x = 40,
∵10×40 = 400,
∴P = $\frac{400}{R}$,当R = 25时,P = $\frac{400}{25}$=16,即当R = 25Ω时,P为16 W.
∵10×40 = 400,
∴P = $\frac{400}{R}$,当R = 25时,P = $\frac{400}{25}$=16,即当R = 25Ω时,P为16 W.
15.(2024广东深圳福田三模)如图,在平面直角坐标系中,等腰△ABC的底边BC在x轴的正半轴上,顶点A在反比例函数y = $\frac{k}{x}$(x>0)的图象上,延长AB交y轴于点D,若BD∶AB = 2∶3,△BOD的面积为$\frac{2}{3}$,则k的值为________.


答案:
答案 5 解析 如图,作AE⊥x轴,垂足为E,连接OA,
∵BD : AB = 2 : 3,△BOD的面积为$\frac{2}{3}$,
∴S△AOB = $\frac{2}{3}$×$\frac{3}{2}$=1,
∵OD//AE,
∴△OBD∽△EBA,
∴$\frac{S_{\triangle OBD}}{S_{\triangle EAB}}$=($\frac{BD}{AB}$)²=$\frac{4}{9}$,
∴S△EAB = $\frac{\frac{2}{3}×9}{4}$=$\frac{3}{2}$,
∴S△OAE = S△AOB + S△EAB = 1+$\frac{3}{2}$=$\frac{5}{2}$,
∵点A在反比例函数图象上,且图象在第一象限,
∴k = 2S△OAE = 5.
答案 5 解析 如图,作AE⊥x轴,垂足为E,连接OA,
∵BD : AB = 2 : 3,△BOD的面积为$\frac{2}{3}$,
∴S△AOB = $\frac{2}{3}$×$\frac{3}{2}$=1,
∵OD//AE,
∴△OBD∽△EBA,
∴$\frac{S_{\triangle OBD}}{S_{\triangle EAB}}$=($\frac{BD}{AB}$)²=$\frac{4}{9}$,
∴S△EAB = $\frac{\frac{2}{3}×9}{4}$=$\frac{3}{2}$,
∴S△OAE = S△AOB + S△EAB = 1+$\frac{3}{2}$=$\frac{5}{2}$,
∵点A在反比例函数图象上,且图象在第一象限,
∴k = 2S△OAE = 5.

16.(2023广东揭阳中考)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为________.
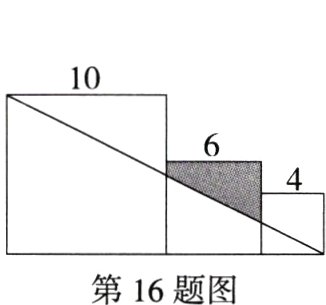

答案:
答案 15 解析 如图,
∵BF//DE,
∴△ABF∽△ADE,
∴$\frac{AB}{AD}$=$\frac{BF}{DE}$,
∵AB = 4,AD = 4 + 6 + 10 = 20,DE = 10,
∴$\frac{4}{20}$=$\frac{BF}{10}$,
∴BF = 2,
∴GF = 6 - 2 = 4,
∵CK//DE,
∴△ACK∽△ADE,
∴$\frac{AC}{AD}$=$\frac{CK}{DE}$,
∵AC = 4 + 6 = 10,AD = 20,DE = 10,
∴$\frac{10}{20}$=$\frac{CK}{10}$,
∴CK = 5,
∴HK = 6 - 5 = 1,
∴阴影部分的面积 = $\frac{1}{2}$(HK + GF)·GH = $\frac{1}{2}$×(1 + 4)×6 = 15.
答案 15 解析 如图,
∵BF//DE,
∴△ABF∽△ADE,
∴$\frac{AB}{AD}$=$\frac{BF}{DE}$,
∵AB = 4,AD = 4 + 6 + 10 = 20,DE = 10,
∴$\frac{4}{20}$=$\frac{BF}{10}$,
∴BF = 2,
∴GF = 6 - 2 = 4,
∵CK//DE,
∴△ACK∽△ADE,
∴$\frac{AC}{AD}$=$\frac{CK}{DE}$,
∵AC = 4 + 6 = 10,AD = 20,DE = 10,
∴$\frac{10}{20}$=$\frac{CK}{10}$,
∴CK = 5,
∴HK = 6 - 5 = 1,
∴阴影部分的面积 = $\frac{1}{2}$(HK + GF)·GH = $\frac{1}{2}$×(1 + 4)×6 = 15.

17.[答案含评分细则](10分)(2024山东济宁金乡一模)如图,点A(3,6),B(6,a)是反比例函数y = $\frac{m}{x}$(m>0)的图象上的两点.
(1)求a的值.
(2)求△AOB的面积.
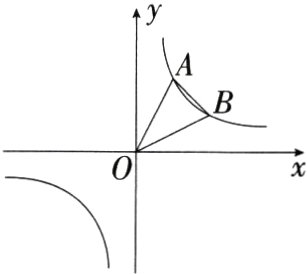
(1)求a的值.
(2)求△AOB的面积.

答案:
解析
(1)把A(3,6)代入y = $\frac{m}{x}$,得m = 18,即y = $\frac{18}{x}$, ………………………… 3分把B(6,a)代入y = $\frac{18}{x}$,可得a = $\frac{18}{6}$=3. ………………………… 5分
(2)如图,过A作AM⊥x轴于M,过B作BN⊥x轴于N,
∵A(3,6),B(6,3),
∴AM = 6,OM = 3,ON = 6,BN = 3, …………………… 7分
∴S△AOB = S△AMO + S梯形AMNB - S△BNO= $\frac{1}{2}$×3×6+$\frac{1}{2}$×(6 + 3)×(6 - 3)-$\frac{1}{2}$×6×3 = $\frac{27}{2}$. …… ………………………… 10分
解析
(1)把A(3,6)代入y = $\frac{m}{x}$,得m = 18,即y = $\frac{18}{x}$, ………………………… 3分把B(6,a)代入y = $\frac{18}{x}$,可得a = $\frac{18}{6}$=3. ………………………… 5分
(2)如图,过A作AM⊥x轴于M,过B作BN⊥x轴于N,

∵A(3,6),B(6,3),
∴AM = 6,OM = 3,ON = 6,BN = 3, …………………… 7分
∴S△AOB = S△AMO + S梯形AMNB - S△BNO= $\frac{1}{2}$×3×6+$\frac{1}{2}$×(6 + 3)×(6 - 3)-$\frac{1}{2}$×6×3 = $\frac{27}{2}$. …… ………………………… 10分
查看更多完整答案,请扫码查看


