《2025年5年中考3年模拟九年级数学下册人教版》

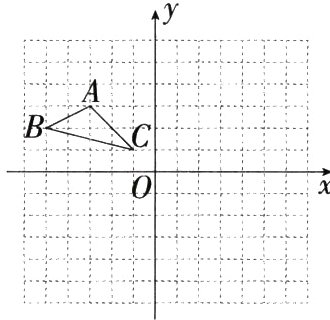
17.［答案含评分细则］(10分)(2024江苏南通海安期末)平面直角坐标系xOy中，A(-3,3)，B(-5,2)，C(-1,1).
(1)以点C为位似中心，在网格图中画出△A₁B₁C，使它与△ABC的相似比为2 : 1，并写出点A的对应点A₁的坐标.
(2)画出△ABC绕点C逆时针旋转90°后的图形△A₂B₂C.
(3)在(2)的条件下，求点B经过的路径长.

答案：
17解析 （1）△A₁B₁C如图所示， …… 3分
点A₁的坐标为（3，-3）. …… 4分

（2）△A₂B₂C如图所示. …… 7分
（3）由勾股定理得BC = $\sqrt{4^{2}+1^{2}}$ = $\sqrt{17}$，
∴点B经过的路径长为$\frac{90\pi×\sqrt{17}}{180}$ = $\frac{\sqrt{17}}{2}\pi$. …… 10分

18.［答案含评分细则］(10分)(2022山东聊城中考)聊城市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔，塔旁有一棵唐代古槐，称为“宋塔唐槐”.某数学兴趣小组利用无人机测量古槐的高度，如图所示，当无人机从位于塔基B点与古槐底D点之间的地面H点，竖直起飞到正上方45米处的E点时，测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°(B，H，D三点在同一直线上).已知塔高为39米，塔基B点与树底D点的水平距离为20米，求古槐的高度(结果精确到1米).
(参考数据：sin26.6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.50，sin76°≈0.97，cos76°≈0.24，tan76°≈4.01)

答案：
18解析 如图，过点A作AM⊥EH于M，过点C作CN⊥EH于N，

由题意知AM = BH，CN = DH，AB = MH， … 2分
在Rt△AME中，∠EAM = 26.6°，
∵tan∠EAM = $\frac{EM}{AM}$，
∴AM = $\frac{EM}{\tan∠EAM}$ = $\frac{EH - MH}{\tan 26.6^{\circ}}$≈$\frac{45 - 39}{0.5}$ = 12米， … 4分
∴BH = AM = 12米，
∵BD = 20米，
∴DH = BD - BH = 8米，
∴CN = 8米， … 7分
在Rt△ENC中，∠ECN = 76°，
∵tan∠ECN = $\frac{EN}{CN}$，
∴EN = CN·tan∠ECN≈8×4.01 = 32.08米， … 9分
∴CD = NH = EH - EN = 12.92≈13米，
即古槐的高度约为13米. … 10分

19.［答案含评分细则］(10分)(2023湖北潜江模拟)如图，在平面直角坐标系中，∠AOB = 90°，点A，B分别在函数y = $\frac{k}{x}$(x＜0)，y = $\frac{2}{x}$(x＞0)的图象上.
(1)过点B作BE⊥x轴于点E，则△BOE的面积为________(直接写出结果).
(2)若tan∠OAB = 2，求k的值.

答案：
19解析 （1）1. … 3分
详解：
∵点B在y = $\frac{2}{x}$（x＞0）的图象上，且BE⊥x轴，
∴S△BOE = $\frac{2}{2}$ = 1.
（2）如图，过点A作AF⊥x轴于点F，

则有∠AFO = 90°，
∴∠FAO + ∠AOF = 90°，
∵∠AOB = 90°，
∴∠AOF + ∠BOE = 90°. … 4分
∴∠FAO = ∠BOE，
∴△AOF∽△OBE， … 6分
∴$\frac{S_{\triangle BOE}}{S_{\triangle AOF}}$ = （$\frac{BO}{OA}$）² = （tan∠OAB）² = 4，
∴S△AOF = $\frac{1}{4}$S△BOE = $\frac{1}{4}$， … 8分
∴$\frac{1}{2}$|k| = $\frac{1}{4}$，又k＜0，
∴k = -$\frac{1}{2}$. … 10分

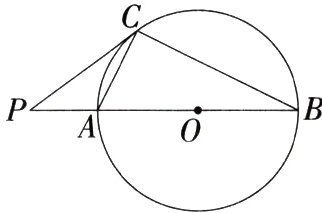
20.［答案含评分细则］(10分)(2024江苏盐城阜宁期末)如图，O为线段PB上一点，以点O为圆心，OB长为半径的⊙O交PB于点A，点C在⊙O上，连接AC，BC，PC，满足PC² = PA·PB.
(1)求证：PC是⊙O的切线.
(2)若AB = 2PA，求$\frac{AC}{BC}$的值.

答案：
20解析 （1）证明：连接OC，

∵PC² = PA·PB，
∴$\frac{PA}{PC}$ = $\frac{PC}{PB}$，
∵∠P = ∠P，
∴△PAC∽△PCB，
∴∠PCA = ∠B， … 2分
∵∠ACB = 90°，
∴∠CAB + ∠B = 90°，
∵OA = OC，
∴∠CAB = ∠OCA，
∴∠PCA + ∠OCA = 90°，即∠PCO = 90°，
∴OC⊥PC， … 4分
∴PC是⊙O的切线. … 5分
（2）
∵AB = 2PA，
∴OC = OA = PA，
∴PO = 2PA， … 7分
∵OC⊥PC，
∴PC = $\sqrt{PO^{2}-OC^{2}}$ = $\sqrt{3}$PA，
∵△PAC∽△PCB，
∴$\frac{AC}{BC}$ = $\frac{PC}{PB}$ = $\frac{\sqrt{3}PA}{3PA}$ = $\frac{\sqrt{3}}{3}$. … 10分