《2025年5年中考3年模拟九年级数学下册人教版》

1.(2024四川内江中考)2024年6月5日是二十四节气的芒种，二十四节气是中国劳动人民独创的文化遗产，能反映季节的变化，指导农事活动.下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”，其中是中心对称图形的是( )

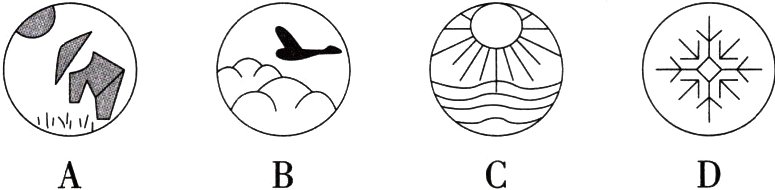
答案： D D中，能找到一个点，使图形绕着该点旋转180°后与原图形重合，故选D.

2.(情境题·中华优秀传统文化)(2024广西中考)榫卯是我国传统建筑及家具的基本构件.燕尾榫是“万榫之母”，为了防止受拉力时脱开，榫头成梯台形，形似燕尾.如图所示的是燕尾榫的带榫头部分，它的主视图是(M9229002)( )

答案： A 从正面看，可得选项A的图形. 故选A.

3.(2024上海中考)以下一元二次方程有两个相等实数根的是( )
A.$x^{2}-6x = 0$
B.$x^{2}-9 = 0$
C.$x^{2}-6x + 6 = 0$
D.$x^{2}-6x + 9 = 0$

答案： D $x^{2}-6x = 0$，解得$x = 0$或$x = 6$，
∴该方程有两个不相等的实数根，故A不符合题意；$x^{2}-9 = 0$，解得$x = 3$或$x=-3$，
∴该方程有两个不相等的实数根，故B不符合题意；由$x^{2}-6x + 6 = 0$知$\Delta=36 - 24 = 12＞0$，
∴该方程有两个不相等的实数根，故C不符合题意；由$x^{2}-6x + 9 = 0$知$\Delta=36 - 36 = 0$，
∴该方程有两个相等实数根，故D符合题意. 故选D.

4.(新独家原创)如图，$A_{1}B_{1}$是线段$AB$在投影面上的正投影，已知$AB = a$，$\angle ABB_{1}=\alpha(90^{\circ}＜\alpha＜180^{\circ})$，$A_{1}B_{1}=b$，则$b$与$a$的关系为( )

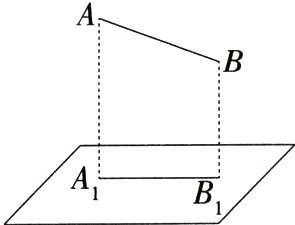
A.$b = a\cdot\sin\alpha$
B.$b = a\cdot\cos\alpha$
C.$b = a\cdot\cos(\alpha - 90^{\circ})$
D.$b = a\cdot\sin(\alpha - 90^{\circ})$

答案：
C 如图，过点B作$BC\perp AA_{1}$于C，$\because A_{1}B_{1}$是线段AB在投影面上的正投影，$\therefore AA_{1}\perp A_{1}B_{1}$，$BB_{1}\perp A_{1}B_{1}$，$\therefore$四边形$A_{1}B_{1}BC$为矩形，$\therefore BC = A_{1}B_{1}=b$，$\angle CBB_{1}=90^{\circ}$，$\therefore\angle ABC=\angle ABB_{1}-\angle CBB_{1}=\alpha - 90^{\circ}$. 在$Rt\triangle ABC$中，$BC = AB\cdot\cos\angle ABC$，$\therefore b = a\cdot\cos(\alpha - 90^{\circ})$. 故选C.

5.(2024四川宜宾中考)如图，$AB$是$\odot O$的直径，若$\angle CDB = 60^{\circ}$，则$\angle ABC$的度数等于( )

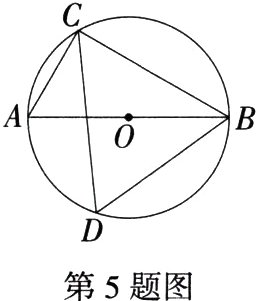
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$

答案： A $\because AB$是$\odot O$的直径，$\therefore\angle ACB = 90^{\circ}$，$\because\angle CDB = 60^{\circ}$，$\therefore\angle A=\angle CDB = 60^{\circ}$，$\therefore\angle ABC = 90^{\circ}-\angle A = 30^{\circ}$. 故选A.

6.(新考法)(2023河北衡水二模)如图，点$M$，$N$，$P$，$Q$，$T$均为坐标系中$2\times2$的正方形网格的格点(网格的横线都与$x$轴平行，纵线都与$y$轴平行，每个小正方形的边长为1个单位长度)，点$N$的坐标为$(2,2)$，在反比例函数$y=\frac{k}{x}(x ＞ 0)$中的常数$k$的值从1逐渐增大到9的过程中，关于其图象$l$依次经过的格点的顺序，下列说法正确的是( )

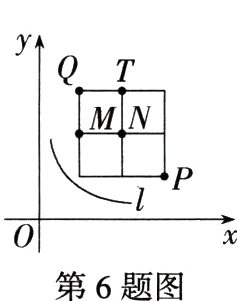
A.点$M\rightarrow$点$P\rightarrow$同时经过点$N$，$Q\rightarrow$点$T$
B.点$M\rightarrow$点$N\rightarrow$同时经过点$P$，$Q\rightarrow$点$T$
C.点$M\rightarrow$同时经过点$P$，$Q\rightarrow$点$N\rightarrow$点$T$
D.点$P\rightarrow$点$M\rightarrow$同时经过点$N$，$Q\rightarrow$点$T$

答案： C 由题得N(2,2)，M(1,2)，Q(1,3)，T(2,3)，P(3,1)，$\because2\times2 = 4，$$1\times2 = 2，$$1\times3 = 3，$$2\times3 = 6，$$3\times1 = 3，$2

7.(情境题·数学文化)(2023四川乐山中考)我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”，如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25，小正方形面积为1，则$\sin\theta=$(M9228001)( )

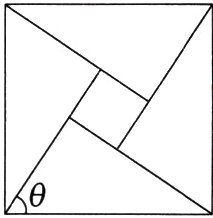
A.$\frac{4}{5}$
B.$\frac{3}{5}$
C.$\frac{2}{5}$
D.$\frac{1}{5}$

答案： A 设大正方形的边长为$c$，直角三角形的短直角边长为$a$，长直角边长为$b$，由题意，得$c^{2}=25$，$b - a=\sqrt{1}=1$，$a^{2}+b^{2}=c^{2}$，$\therefore a = 3$，$b = 4$，$c = 5$，$\therefore\sin\theta=\frac{b}{c}=\frac{4}{5}$. 故选A.

8.(跨物理·杠杆原理)(2023山西朔州山阴模拟)公元前3世纪，古希腊科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即阻力×阻力臂 = 动力×动力臂，小伟欲用撬棍撬动一块石头，已知在某一平衡状态下，阻力和阻力臂分别是1 000 N和0.4 m，若动力$F_{1}＞F_{2}$(单位：N)，则动力臂$l_{1}$与$l_{2}$(单位：m)的数量关系为(M9226004)( )
A.$l_{1}＜l_{2}$
B.$l_{1}＞l_{2}$
C.$l_{1}=l_{2}$
D.无法确定

答案： $A \because$阻力×阻力臂 = 动力×动力臂，$\therefore$动力F（单位：N）与动力臂l（单位：m）的函数解析式为$1000\times0.4 = Fl，$则$l=\frac{400}{F}(F＞0)，$$\therefore$动力臂l是动力F的反比例函数，且动力臂l随动力F的增大而减小，$\because$动力$F_{1}＞F_{2}，$$\therefore$动力臂$l_{1}$