《2025年5年中考3年模拟九年级数学下册人教版》

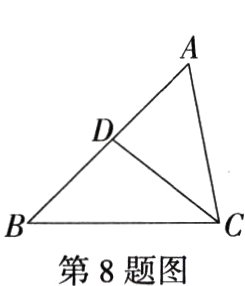
8.(2023上海徐汇模拟)如图所示,给出下列条件:
①∠B = ∠ACD;②∠ADC = ∠ACB;③$\frac{AC}{CD}=\frac{AB}{BC}$;④$AC^{2}=AD·AB$.其中能够判定△ABC∽△ACD的个数为(M9227004) ( )

A.1
B.2
C.3
D.4

答案： ①
∵∠B=∠ACD，∠DAC=∠BAC，
∴△ABC∽△ACD，故①符合题意;②
∵∠ADC=∠ACB，∠DAC=∠BAC，
∴△ABC∽△ACD，故②符合题意;③$\frac{AC}{CD}$=$\frac{AB}{BC}$，但∠ACD和∠ABC不一定相等，因此不能判定△ABC∽△ACD，故③不符合题意;④
∵AC²=AD·AB，
∴$\frac{AC}{AD}$=$\frac{AB}{AC}$，又
∵∠DAC=∠BAC，
∴△ABC ∽△ACD，故④符合题意.综上所述，能够判定△ABC ∽△ACD的条件的个数为3.故选C.

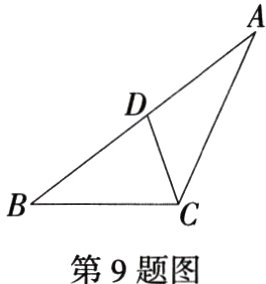
9.(2024山东济南济阳期末)如图,在△ABC中,点D是AB边上一点,连接CD.已知AD = 4,BD = 5,AC = 6,CD = 3,那么线段BC的长度是________.(M9227004)

答案： 答案　$\frac{9}{2}$
解析
∵AD=4，BD=5，AC=6，
∴$\frac{AC}{AD}$=$\frac{6}{4}$=$\frac{3}{2}$，$\frac{AB}{AC}$=$\frac{4 + 5}{6}$=$\frac{3}{2}$，
∴$\frac{AC}{AD}$=$\frac{AB}{AC}$，
∵∠CAD=∠BAC，
∴△ABC∽△ACD，
∴$\frac{CD}{BC}$=$\frac{2}{3}$，
∵CD=3，
∴BC=$\frac{9}{2}$.

10.(2024云南红河州二模)如图,AB是☉O的直径,点C在☉O上,延长BA至点D,使$CD^{2}=AD·BD$.(M9227004)
(1)求证:CD是☉O的切线.
(2)若☉O的半径为$\sqrt{5}$,BC = 4,求$\frac{AB}{CD}$的值.

答案：
解析　
(1)证明:连接OC.
　　　　　　
∵AB是⊙O的直径，
∴∠ACB=90°，即∠BAC+∠B=90°.
∵CD²=AD·BD，
∴$\frac{CD}{BD}$=$\frac{AD}{CD}$.
又
∵∠ADC=∠CDB，
∴△ADC∽△CDB，
∴∠ACD=∠B，
∵OA=OC，
∴∠BAC=∠OCA.
∴∠OCA+∠ACD=90°，即∠OCD=90°.
∴OC⊥CD.
∵OC是⊙O的半径，
∴CD是⊙O的切线.
(2)由题可知AB = 2$\sqrt{5}$.
在Rt△ABC中，∠ACB=90°，AC=$\sqrt{(2\sqrt{5})^{2}-4^{2}}$=2.
由
(1)知△ADC∽△CDB，OC⊥CD，
∴$\frac{CD}{BD}$=$\frac{AD}{CD}$=$\frac{AC}{CB}$=$\frac{2}{4}$=$\frac{1}{2}$.
设AD=x，则CD=2x，
在Rt△OCD中，OC²+CD²=OD²，即($\sqrt{5}$)²+(2x)²=($\sqrt{5}$+x)²，解得x₁=$\frac{2\sqrt{5}}{3}$，x₂=0(舍去)，
∴CD=$\frac{4\sqrt{5}}{3}$，
∴$\frac{AB}{CD}$=$\frac{3}{2}$.

11.(2024浙江杭州西湖期中)如图,在矩形ABCD中,$BD = 2\sqrt{3}$.对角线AC与BD相交于点O,过点D作AC的垂线,交AC于点E,AE = 3CE.则$DE^{2}$的值为 ( )

A.4
B.$2\sqrt{3}$
C.$\frac{9}{4}$
D.$4\sqrt{3}$

答案：
∵四边形ABCD是矩形，
∴∠ADC=90°，AC=BD = 2$\sqrt{3}$，
∵AE = 3CE，
∴AE=$\frac{3}{4}$AC=$\frac{3}{2}\sqrt{3}$，CE=$\frac{1}{4}$AC=$\frac{\sqrt{3}}{2}$.由射影定理相似模型可得△ADE∽△DCE，
∴$\frac{DE}{CE}$=$\frac{AE}{DE}$，
∴DE²=AE·CE=$\frac{3}{2}\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{9}{4}$.故选C.

12.(2024北京石景山期中)如图,在Rt△ABC中,∠BAC = 90°,AD⊥BC于点D,AB = 3,BC = 5,则BD = ________.(M9227004)

答案： 答案　1.8
解析
∵AD⊥BC，
∴∠ADB=90°，
∴∠ADB=∠BAC，又
∵∠B=∠B，
∴△ABD∽△CBA，
∴$\frac{AB}{BD}$=$\frac{BC}{AB}$，即$\frac{3}{BD}$=$\frac{5}{3}$，解得BD=1.8.

13.(2024黑龙江大庆肇源期中)如图,CE是Rt△ABC的斜边AB上的高,BG⊥AP.
求证:$CE^{2}=ED·EP$.(M9227004)

答案： 证明
∵CE是Rt△ABC的斜边AB上的高，
∴△ACE∽△CBE，
∴$\frac{CE}{AE}$=$\frac{BE}{CE}$，即CE²=AE·BE.
∵CE是Rt△ABC的斜边AB上的高，BG⊥AP，
∴∠P+∠PAE=90°，∠DBE+∠PAE=90°，
∴∠P=∠DBE，
又
∵∠AEP=∠DEB=90°，
∴△AEP∽△DEB，
∴$\frac{AE}{DE}$=$\frac{EP}{EB}$，即AE·BE=ED·EP，
又
∵CE²=AE·BE，
∴CE²=ED·EP.

14.方程思想(2022四川达州中考)如图,点E在矩形ABCD的AB边上,将△ADE沿DE翻折,点A恰好落在BC边上的点F处,若CD = 3BF,BE = 4,则AD的长为(M9227004) ( )

A.9
B.12
C.15
D.18

答案：
∵四边形ABCD是矩形，
∴AD=BC，∠A=∠B=∠C=90°.由翻折可得AD=DF=BC，∠A=∠DFE=90°，
∴∠BFE+∠DFC=∠BFE+∠BEF=90°，
∴∠BEF=∠CFD，
∴△BEF∽△CFD，
∴$\frac{BF}{CD}$=$\frac{BE}{CF}$，
∵CD=3BF，
∴CF=3BE=12，设BF=x，则CD=3x，DF=BC=x+12，
∵∠C=90°，
∴Rt△CDF中，CD²+CF²=DF²，
∴(3x)²+12²=(x+12)²，解得x=3(舍去x=0)，
∴AD=DF=3+12=15.故选C.