第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1.(2024安徽合肥庐江月考)如图,下列条件不能判定△ABC与△ADE相似的是 ( )

A.$\frac{AE}{AC}=\frac{AD}{AB}$
B.∠B = ∠ADE
C.∠C = ∠AED
D.AE·BC = AC·DE

A.$\frac{AE}{AC}=\frac{AD}{AB}$
B.∠B = ∠ADE
C.∠C = ∠AED
D.AE·BC = AC·DE
答案:
由题图知∠EAD=∠BAC.A.符合两边夹角定理,故A能判定△ABC与△ADE相似;B.符合两角定理,故B能判定△ABC与△ADE相似;C.符合两角定理,故C能判定△ABC与△ADE相似;D.由AE·BC = AC·DE,得$\frac{AE}{AC}$=$\frac{DE}{BC}$,不符合两边夹角定理,故D不能判定△ABC与△ADE相似.故选D.
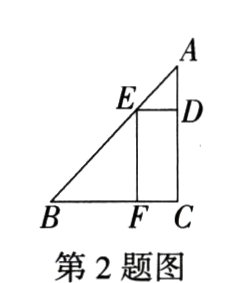
2.(2023湖北恩施州中考)如图,在△ABC中,DE//BC分别交AC,AB于点D,E,EF//AC交BC于点F,$\frac{AE}{BE}=\frac{2}{5}$,BF = 8,则DE的长为 ( )
A.$\frac{16}{5}$
B.$\frac{16}{7}$
C.2
D.3

A.$\frac{16}{5}$
B.$\frac{16}{7}$
C.2
D.3
答案:
∵DE//BC,EF//AC,
∴四边形EFCD是平行四边形,
∴DE=CF,设DE=CF=x,
∵BF=8,
∴BC=BF+CF=8+x,
∵DE//BC,
∴△AED∽△ABC,
∴$\frac{AE}{AB}$=$\frac{DE}{BC}$,
∵$\frac{AE}{BE}$=$\frac{2}{5}$,
∴$\frac{AE}{AB}$=$\frac{2}{7}$,
∴$\frac{DE}{BC}$=$\frac{2}{7}$,即$\frac{x}{8 + x}$=$\frac{2}{7}$,解得x=$\frac{16}{5}$,即DE的长为$\frac{16}{5}$.故选A.
∵DE//BC,EF//AC,
∴四边形EFCD是平行四边形,
∴DE=CF,设DE=CF=x,
∵BF=8,
∴BC=BF+CF=8+x,
∵DE//BC,
∴△AED∽△ABC,
∴$\frac{AE}{AB}$=$\frac{DE}{BC}$,
∵$\frac{AE}{BE}$=$\frac{2}{5}$,
∴$\frac{AE}{AB}$=$\frac{2}{7}$,
∴$\frac{DE}{BC}$=$\frac{2}{7}$,即$\frac{x}{8 + x}$=$\frac{2}{7}$,解得x=$\frac{16}{5}$,即DE的长为$\frac{16}{5}$.故选A.
3.方程思想(2024江苏连云港灌南二模)如图,在△ABC中,BD平分∠ABC,DE//BC交AB于点E,若AB = 6,BC = 4,则DE = ________.


答案:
答案 $\frac{12}{5}$
解析
∵BD平分∠ABC,
∴∠EBD=∠CBD.
∵DE//BC,
∴∠EDB=∠CBD,
∴∠EBD=∠EDB,
∴DE=BE.设DE=BE=x,
∵AB=6,
∴AE=6−x.
∵DE//BC,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}$=$\frac{AE}{AB}$,即$\frac{x}{4}$=$\frac{6−x}{6}$,解得x=$\frac{12}{5}$,即DE=$\frac{12}{5}$.
解析
∵BD平分∠ABC,
∴∠EBD=∠CBD.
∵DE//BC,
∴∠EDB=∠CBD,
∴∠EBD=∠EDB,
∴DE=BE.设DE=BE=x,
∵AB=6,
∴AE=6−x.
∵DE//BC,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}$=$\frac{AE}{AB}$,即$\frac{x}{4}$=$\frac{6−x}{6}$,解得x=$\frac{12}{5}$,即DE=$\frac{12}{5}$.
4.(2024江苏扬州邗江二模)如图,四边形ABCD中,∠ABC = 90°,DE⊥BC于点E,EF = FC,DE交AF于点G,且AF//BC.(M9227004)
求证:
(1)EC = 2GF.
(2)BG = AD.
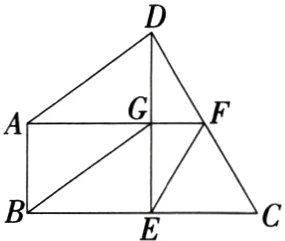
求证:
(1)EC = 2GF.
(2)BG = AD.

答案:
证明
(1)
∵DE⊥BC于点E,
∴∠CED=90°,
∴∠FED+∠FEC=90°,∠FDE+∠C=90°,
∵EF=FC,
∴∠FEC=∠C,
∴∠FED=∠FDE,
∴EF=FD,
∴FD=FC=$\frac{1}{2}$CD,
∵AF//BC,
∴GF//EC,
∴△DGF ∽△DEC,
∴$\frac{GF}{EC}$=$\frac{FD}{CD}$=$\frac{1}{2}$,
∴EC=2GF.
(2)
∵∠CED=∠ABC=90°,
∴GE//AB,
∵AG//BE,
∴四边形ABEG是平行四边形,
∴AB=GE,
∵GF//EC,
∴$\frac{GD}{GE}$=$\frac{FD}{FC}$=1,
∴GD=GE,
∴GD=AB,
∵GD//AB,
∴四边形ABGD是平行四边形,
∴BG=AD.
(1)
∵DE⊥BC于点E,
∴∠CED=90°,
∴∠FED+∠FEC=90°,∠FDE+∠C=90°,
∵EF=FC,
∴∠FEC=∠C,
∴∠FED=∠FDE,
∴EF=FD,
∴FD=FC=$\frac{1}{2}$CD,
∵AF//BC,
∴GF//EC,
∴△DGF ∽△DEC,
∴$\frac{GF}{EC}$=$\frac{FD}{CD}$=$\frac{1}{2}$,
∴EC=2GF.
(2)
∵∠CED=∠ABC=90°,
∴GE//AB,
∵AG//BE,
∴四边形ABEG是平行四边形,
∴AB=GE,
∵GF//EC,
∴$\frac{GD}{GE}$=$\frac{FD}{FC}$=1,
∴GD=GE,
∴GD=AB,
∵GD//AB,
∴四边形ABGD是平行四边形,
∴BG=AD.
5.(2023陕西中考)如图,DE是△ABC的中位线,点F在DB上,DF = 2BF,连接EF并延长,与CB的延长线相交于点M.若BC = 6,则线段CM的长为(M9227004) ( )
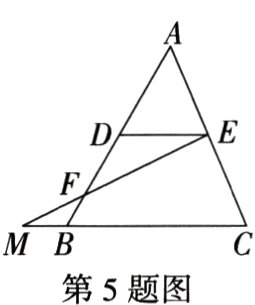
A.$\frac{13}{2}$
B.7
C.$\frac{15}{2}$
D.8

A.$\frac{13}{2}$
B.7
C.$\frac{15}{2}$
D.8
答案:
∵DE是△ABC的中位线,
∴DE//BC,DE=$\frac{1}{2}$BC=$\frac{1}{2}$×6 = 3,
∴△DEF∽△BMF,
∴$\frac{DE}{BM}$=$\frac{DF}{BF}$=$\frac{2BF}{BF}$=2,
∴BM=$\frac{3}{2}$,
∴CM=BC+BM=$\frac{15}{2}$.故选C.
∵DE是△ABC的中位线,
∴DE//BC,DE=$\frac{1}{2}$BC=$\frac{1}{2}$×6 = 3,
∴△DEF∽△BMF,
∴$\frac{DE}{BM}$=$\frac{DF}{BF}$=$\frac{2BF}{BF}$=2,
∴BM=$\frac{3}{2}$,
∴CM=BC+BM=$\frac{15}{2}$.故选C.
6.(2024江苏无锡一模)如图,矩形ABCD为☉O的内接四边形,AB = 2,BC = 3,E为BC上一点,且BE = 1,延长AE交☉O于点F,则线段AF的长为________.


答案:
答案 $\frac{7\sqrt{5}}{5}$
解析 如图,连接CF,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AE=$\sqrt{AB^{2}+BE^{2}}$=$\sqrt{2^{2}+1^{2}}$=$\sqrt{5}$.
∵BC=3,BE=1,
∴CE=2.
∵∠ABC与∠CFA都为$\overset{\frown}{ADC}$所对的圆周角,
∴∠ABE=∠CFE.
∵∠AEB=∠CEF,
∴△ABE∽△CFE,
∴$\frac{AE}{CE}$=$\frac{BE}{FE}$,
∴FE=$\frac{BE·CE}{AE}$=$\frac{1×2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∴AF=AE+FE=$\frac{7\sqrt{5}}{5}$.

答案 $\frac{7\sqrt{5}}{5}$
解析 如图,连接CF,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AE=$\sqrt{AB^{2}+BE^{2}}$=$\sqrt{2^{2}+1^{2}}$=$\sqrt{5}$.
∵BC=3,BE=1,
∴CE=2.
∵∠ABC与∠CFA都为$\overset{\frown}{ADC}$所对的圆周角,
∴∠ABE=∠CFE.
∵∠AEB=∠CEF,
∴△ABE∽△CFE,
∴$\frac{AE}{CE}$=$\frac{BE}{FE}$,
∴FE=$\frac{BE·CE}{AE}$=$\frac{1×2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∴AF=AE+FE=$\frac{7\sqrt{5}}{5}$.

7.(2024黑龙江大庆肇源期中)如图,在□ABCD中,E为边BC上一点,连接AE并延长交DC的延长线于点M,交BD于点G,过点G作GF//AD交DC于点F,$\frac{DF}{FC}=\frac{3}{2}$.(M9227004)
(1)若BD = 20,求BG的长.
(2)求$\frac{CM}{MD}$的值.
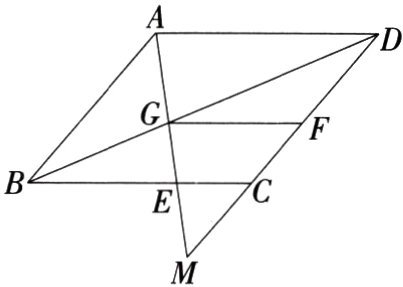
(1)若BD = 20,求BG的长.
(2)求$\frac{CM}{MD}$的值.

答案:
解析
(1)
∵GF//AD,AD//BC,
∴GF//BC,
∴$\frac{BG}{GD}$=$\frac{FC}{DF}$=$\frac{2}{3}$,
∴$\frac{BG}{GD+BG}$=$\frac{BG}{BD}$=$\frac{2}{5}$,
∵BD=20,
∴BG=20×$\frac{2}{5}$=8.
(2)
∵BC//AD,
∴△BEG∽△DAG,
∴$\frac{BE}{AD}$=$\frac{BG}{GD}$=$\frac{2}{3}$,
∵AD=BC,
∴$\frac{EC}{AD}$=$\frac{BC−BE}{AD}$=1 - $\frac{2}{3}$=$\frac{1}{3}$,
∵AD//BC,
∴△ECM∽△ADM,
∴$\frac{CM}{MD}$=$\frac{EC}{AD}$=$\frac{1}{3}$.
(1)
∵GF//AD,AD//BC,
∴GF//BC,
∴$\frac{BG}{GD}$=$\frac{FC}{DF}$=$\frac{2}{3}$,
∴$\frac{BG}{GD+BG}$=$\frac{BG}{BD}$=$\frac{2}{5}$,
∵BD=20,
∴BG=20×$\frac{2}{5}$=8.
(2)
∵BC//AD,
∴△BEG∽△DAG,
∴$\frac{BE}{AD}$=$\frac{BG}{GD}$=$\frac{2}{3}$,
∵AD=BC,
∴$\frac{EC}{AD}$=$\frac{BC−BE}{AD}$=1 - $\frac{2}{3}$=$\frac{1}{3}$,
∵AD//BC,
∴△ECM∽△ADM,
∴$\frac{CM}{MD}$=$\frac{EC}{AD}$=$\frac{1}{3}$.
查看更多完整答案,请扫码查看


