《2025年5年中考3年模拟九年级数学下册人教版》

9.(2024 江苏南京雨花台月考)写出一个三视图中主视图、左视图、俯视图完全相同的几何体名称：________.

答案： 答案　球(答案不唯一) 解析　球的主视图、左视图、俯视图为全等的圆.

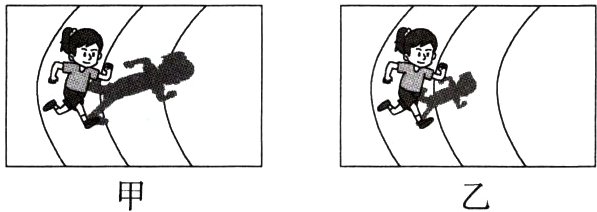
10.某天学校举办了运动会，小红先参加了校运动会女子 100 m 比赛，过一段时间又参加了女子400 m 比赛，比赛都在上午进行，下图是摄影师在同一位置拍摄小红的两张照片，那么________(填“甲”或“乙”)照片是在小红参加 400 m 比赛时拍摄的.

答案： 答案　乙 解析　易知在太阳光下从早晨到中午物体的影长由长变短，
∵比赛都在上午进行，先进行的是100m比赛，
∴影子较长的甲照片是参加100m比赛时拍摄的，影子较短的乙照片是参加400m比赛时拍摄的.

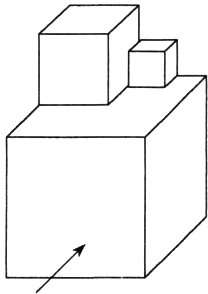
11.(2023 江苏扬州高邮期末)用三个大小不等的正方体拼成了一个如图所示的几何体，若该几何体的主视图、左视图和俯视图的面积分别为 S₁、S₂、S₃，则 S₁、S₂、S₃的大小关系是________(用“＜”连接).

答案： 答案$　S_{3}$

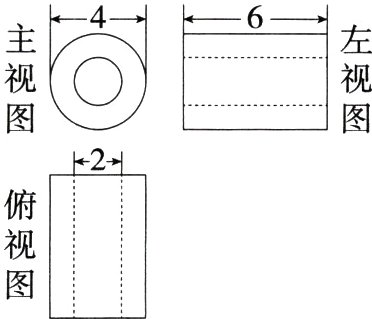
12.(2024 山东东营一模)如图所示的是一个由铁铸灌成的几何体的三视图，根据图中所标数据，铸灌这个几何体需要的铁的体积为________.(M9229003)

答案： 答案　$18\pi$解析　由三视图可得几何体是空心圆柱，其底面的小圆半径是1，大圆半径是2，故这个几何体的体积为$6\times2^{2}\pi-6\times\pi=24\pi-6\pi=18\pi$，即铸灌这个几何体需要的铁的体积为$18\pi$.

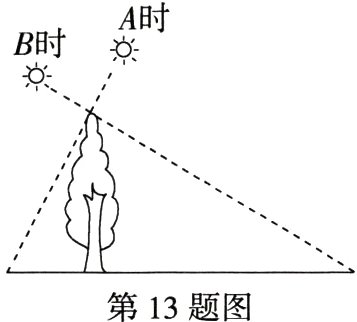
13.(2022 贵州遵义桐梓模拟)如图，在 A 时测得某树的影长为 4 m，在 B 时测得该树的影长为 16 m，若两次日照的光线互相垂直，则树的高度为________.(M9229001)

答案：
答案　8m 解析　如图,过点C作$CD\perp EF$，
∴ $\angle EDC=\angle CDF = 90^{\circ}$，又 $\angle ECF = 90^{\circ}$，
∴ $\angle E+\angle ECD=\angle ECD+\angle DCF = 90^{\circ}$，
∴ $\angle E=\angle DCF$，
∴ $Rt\triangle EDC\sim Rt\triangle CDF$，
∴ $\frac{ED}{DC}=\frac{DC}{FD}$，即$DC^{2}=ED\cdot FD$，又$DE = 4$，$FD = 16$，
∴ $DC^{2}=64$，
∴ $DC = 8$，即树的高度为8m.

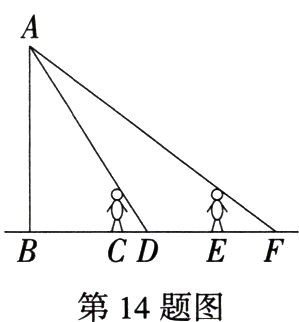
14.(2024 上海黄浦期中)如图，小红晚上由路灯 A下的 B 处走到 C 处时，测得影子 CD 的长为1米，继续往前走 2.5 米到达 E 处时，测得影子EF 的长为 2 米，已知小红的身高是 1.5 米，那么路灯 A 离地面的高度 AB 为________米.

答案：
答案　5.25 解析　如图，
∵ $Rt\triangle DCG\sim Rt\triangle DBA$，$Rt\triangle FEH\sim Rt\triangle FBA$，
∴ $\frac{CD}{BD}=\frac{CG}{AB}$，$\frac{EF}{BF}=\frac{EH}{AB}$，
∵ $\frac{EH}{AB}=\frac{CG}{AB}$，
∴ $\frac{CD}{BD}=\frac{EF}{BF}$，设$AB = x$米，$BC = y$米，
∵ $CD = 1$米，$CE = 2.5$米，$EF = 2$米，
∴ $\frac{1}{y + 1}=\frac{2}{y + 4.5}$，解得$y = 2.5$，
∵ $\frac{CD}{BD}=\frac{CG}{AB}$，$CG = 1.5$米，
∴ $\frac{1}{3.5}=\frac{1.5}{x}$，解得$x = 5.25$.
∴ $AB = 5.25$米.

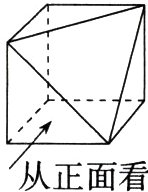
15.(9分)(2024 辽宁阜新期末)画出如图所示的几何体的三视图.(M9229002)

答案：
解析　三视图如图所示:

16.(9分)如图，AB 和 DE 是直立在地面上的两根立柱.AB=7 m，某一时刻 AB 在阳光下的投影BC=4 m.(M9229001)
(1)请你在图中画出此时 DE 在阳光下的投影.
(2)在测量 AB 的投影长时，同时测量出 DE 在阳光下的投影长为 8 m，计算 DE 的长.

答案：
解析　
(1)如图,连接AC,过点D作$DF// AC$，交直线BC于点F,线段EF即为DE的投影.
(2)
∵ $AC// DF$，
∴ $\angle ACB=\angle DFE$.
∵ $\angle ABC=\angle DEF = 90^{\circ}$，
∴ $\triangle ABC\sim\triangle DEF$.
∴ $AB:DE=BC:EF$;
∵ $AB = 7$ m，$BC = 4$ m，$EF = 8$ m，
∴ $7:DE=4:8$，
∴ $DE = 14$ m.