《2025年5年中考3年模拟九年级数学下册人教版》

1.(2024河北张家口宣化一模)下列各选项的两个图形中,不是位似图形的是　　　　　　　(　　　)
　　　
　　　　

答案： C 根据位似图形的概念，A、B、D中的两个图形都是位似图形；C中的两个图形对应点的连线不能相交于一点，故不是位似图形.故选C.

2.(2023河北衡水二模)如图,已知△ABC与△DEF位似,且相似比为k.(M9227006)
　(1)k=________.
　　　　　　　　　　　
　(2)位似中心的坐标为________.

答案：
答案
(1)$\frac{1}{2}$
(2)(3,6)
解析
(1)$AB = 2$，$BC = \sqrt{2}$，$AC = \sqrt{1^{2}+3^{2}} = \sqrt{10}$，$DE = 4$，$EF = \sqrt{2^{2}+2^{2}} = 2\sqrt{2}$，$DF = \sqrt{2^{2}+6^{2}} = 2\sqrt{10}$，$\therefore k=\frac{AB}{DE}=\frac{1}{2}$.
(2)如图所示：

位似中心的坐标为(3,6).

3.(2024湖南郴州嘉禾二模)将△ABC的三边按如下方法缩小到原来的$\frac{1}{2}$:如图,任取一点O,连接AO、BO、CO,并取它们的中点D、E、F,得到△DEF,则下列说法错误的是　　　　　(　　　)
　　　　　
　
A.△ABC与△DEF是位似图形
　
B.△ABC与△DEF是相似图形
　
C.△ABC与△DEF的面积之比为4:1
　
D.△ABC与△DEF的周长之比为1:2

答案： D 根据位似图形的概念知$\triangle ABC$与$\triangle DEF$是位似图形，故A说法正确；位似图形也是相似图形，故B说法正确；$\because$将$\triangle ABC$的三边缩小到原来的$\frac{1}{2}$，$\therefore \triangle ABC$与$\triangle DEF$的面积比为4 : 1，$\triangle ABC$与$\triangle DEF$的周长比为2 : 1，故C说法正确，D说法错误.故选D.

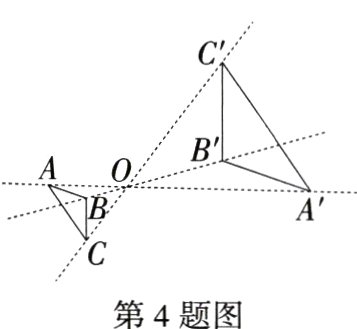
4.(2024贵州铜仁石阡模拟)如图,以点O为位似中心,把△ABC的各边放大为原来的2倍得到△A'B'C',下列说法中,错误的是(M9227006)　　　　(　　　)
　　　　
A.AO:AA'=1:2
　　　　
B.AC//A'C'
　　　　
$C.S_{△ABC}:S_{△A'B'C'}=1:4 $
　　　　
D.A,O,A'三点在同一条直线上
　　　　　

答案： A $\because$以点O为位似中心，把$\triangle ABC$的各边放大为原来的2倍得到$\triangle A'B'C'$，$\therefore A$，$O$，$A'$三点在同一条直线上，$AO:OA' = OC:OC' = 1:2$，$\therefore AO:AA' = 1:3$.$\because \triangle ABC\backsim\triangle A'B'C'$，且相似比为1 : 2，$\therefore S_{\triangle ABC}:S_{\triangle A'B'C'}=1:4$，$\because AO:OA' = OC:OC'$，$\angle AOC = \angle A'OC'$，$\therefore \triangle AOC\backsim\triangle A'OC'$，$\therefore \angle ACO = \angle A'C'O$，$\therefore AC// A'C'$.综上，只有选项A说法错误.故选A.

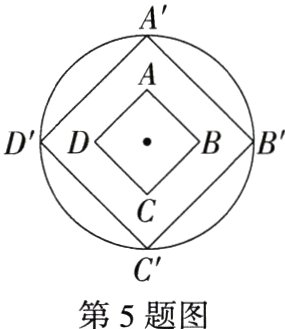
5.(情境题·中华优秀传统文化)(2023山东枣庄山亭期末)《墨子·天志上》记载:“轮匠执其规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的面积为1,以它的对角线的交点为位似中心,作它的位似图形A'B'C'D',若AB:A'B'=1:2,则正方形A'B'C'D'的周长为________.

答案： 答案 8
解析 $\because$正方形ABCD的面积为1，$\therefore AB = 1$，$\therefore$正方形ABCD的周长为4.$\because AB:A'B' = 1:2$，$\therefore \frac{正方形ABCD的周长}{正方形A'B'C'D'的周长}=\frac{1}{2}$，$\therefore$正方形$A'B'C'D'$的周长$=2\times4 = 8$.

6.(2024广西百色田阳一模)如图,在由边长为1个单位长度的小正方形组成的网格中,已知点O、A、B、C均为网格线的交点.(M9227006)
　　　　(1)以点O为位似中心,在网格中画出△ABC 的位似图形$△A_{1}B_{1}C_{1},$使原图形与新图形的相似比为1:2.
$　　　　(2)△A_{1}B_{1}C_{1}$的面积为________.
　　　　　　　　　

答案：
解析
(1)如图所示，$\triangle A_{1}B_{1}C_{1}$就是所求作的三角形.

(2)8.
提示：$S_{\triangle A_{1}B_{1}C_{1}}=4\times6-\frac{1}{2}\times2\times2-\frac{1}{2}\times2\times6-\frac{1}{2}\times4\times4 = 8$.