第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
18.(新考向·项目式学习试题)(10分)(2024甘肃嘉峪关期末)下面是小明进行数学学科项目化学习的内容.
项目主题:测量河流的宽度.
项目探究:河流宽度不能直接测量,需要借助一些工具,比如:小镜子,标杆,皮尺,自制的直角三角形模板,……,各组确定方案后,选择测量工具,画出测量示意图,并进行实地测量,得到具体数据,从而计算出河流的宽度.
项目成果:下面是小明进行交流展示的部分测量方案及测量数据.

请你参与这个项目学习,并完成下列任务.(M9227007)
(1)任务一:请你借助小明的测量数据,计算河流的宽度AB.
(2)任务二:请你写出这个方案中求河流的宽度时用的数学知识:________________(写出一条即可).
(3)任务三:请你再设计一个与小明不同的测量方案,并画图简要说明一下.
项目主题:测量河流的宽度.
项目探究:河流宽度不能直接测量,需要借助一些工具,比如:小镜子,标杆,皮尺,自制的直角三角形模板,……,各组确定方案后,选择测量工具,画出测量示意图,并进行实地测量,得到具体数据,从而计算出河流的宽度.
项目成果:下面是小明进行交流展示的部分测量方案及测量数据.

请你参与这个项目学习,并完成下列任务.(M9227007)
(1)任务一:请你借助小明的测量数据,计算河流的宽度AB.
(2)任务二:请你写出这个方案中求河流的宽度时用的数学知识:________________(写出一条即可).
(3)任务三:请你再设计一个与小明不同的测量方案,并画图简要说明一下.
答案:
解析
(1)由题知BC//DE,
∴△ABC∽△ADE.
∴AB/AD = BC/DE,
又BC = 1.6 m,BD = 10 m,DE = 2.0 m,
∴AB/(AB + 10) = 1.6/2.0,
解得AB = 40 m.
答:河流的宽度AB为40 m.
(2)相似三角形的对应边成比例(答案不唯一,合理即可).
(3)(答案不唯一,合理即可)如图,在河对岸找一个参照物A,站在A的正对面B的位置,沿着河岸走一段距离,到达C处,在C处竖立一标杆,然后继续行走,走到D处,使得CD = BC,再沿着与河岸垂直的方向行走,当走到与A、C共线时停下,位置记为E,这时DE的长度即为河流的宽度.

解析
(1)由题知BC//DE,
∴△ABC∽△ADE.
∴AB/AD = BC/DE,
又BC = 1.6 m,BD = 10 m,DE = 2.0 m,
∴AB/(AB + 10) = 1.6/2.0,
解得AB = 40 m.
答:河流的宽度AB为40 m.
(2)相似三角形的对应边成比例(答案不唯一,合理即可).
(3)(答案不唯一,合理即可)如图,在河对岸找一个参照物A,站在A的正对面B的位置,沿着河岸走一段距离,到达C处,在C处竖立一标杆,然后继续行走,走到D处,使得CD = BC,再沿着与河岸垂直的方向行走,当走到与A、C共线时停下,位置记为E,这时DE的长度即为河流的宽度.

19.(14分)(2024海南儋州期中)如图,在等腰三角形ABC中,AB = AC = 10,BC = 12,点P沿线段AB按A→B方向向终点B运动,点Q沿线段BC按B→C方向向终点C运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,它们分别从点A和点B同时出发,当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t(t>0)秒,请解答下列问题:
(1)如图1,当t为何值时,PQ//AC?
(2)当t为何值时,以点P、B、Q为顶点的三角形与△ABC相似?
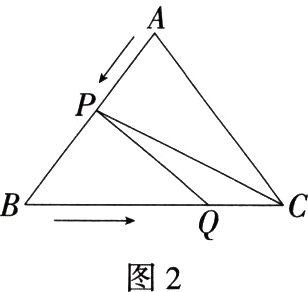
(3)如图2,点P、Q在运动过程中,是否存在这样的t,使得△PCQ的面积等于4?若存在,请求出t的值;若不存在,请说明理由.

(1)如图1,当t为何值时,PQ//AC?
(2)当t为何值时,以点P、B、Q为顶点的三角形与△ABC相似?
(3)如图2,点P、Q在运动过程中,是否存在这样的t,使得△PCQ的面积等于4?若存在,请求出t的值;若不存在,请说明理由.


答案:
解析
(1)当PQ//AC时,△BPQ∽△BAC,
∴BP/AB = BQ/BC.
∵AB = AC = 10,BC = 12,BP = 10 - t,BQ = 2t,
∴(10 - t)/10 = 2t/12,解得t = 15/4,
∴当t = 15/4时,PQ//AC.
(2)
∵∠ABC = ∠PBQ,
∴分以下两种情况:
①△PBQ∽△ABC,同
(1)可得t = 15/4;
②△QBP∽△ABC,
由BQ/AB = BP/BC,得2t/10 = (10 - t)/12,解得t = 50/17.
综上,当t = 15/4或t = 50/17时,以点P、B、Q为顶点的三角形与△ABC相似.
(3)存在.
如图,过P作PE⊥BC,垂足为E,作△ABC的BC边上的高AD,

∵AB = AC = 10,BC = 12,
∴BD = CD = 1/2BC = 6,
∴AD = √(AB² - BD²) = 8,
∵∠BEP = ∠ADB = 90°,∠B = ∠B,
∴△PBE∽△ABD,
∴BP/AB = PE/AD,即(10 - t)/10 = PE/8,
∴PE = 8 - 4t/5,
∴S△PCQ = 1/2×CQ×PE = 1/2×(12 - 2t)×(8 - 4t/5) = 4,
解得t = 5或t = 11,
当t = 5时,经检验符合题意,
当t = 11时,BQ = 22>BC,故不合题意,
∴t = 5.
解析
(1)当PQ//AC时,△BPQ∽△BAC,
∴BP/AB = BQ/BC.
∵AB = AC = 10,BC = 12,BP = 10 - t,BQ = 2t,
∴(10 - t)/10 = 2t/12,解得t = 15/4,
∴当t = 15/4时,PQ//AC.
(2)
∵∠ABC = ∠PBQ,
∴分以下两种情况:
①△PBQ∽△ABC,同
(1)可得t = 15/4;
②△QBP∽△ABC,
由BQ/AB = BP/BC,得2t/10 = (10 - t)/12,解得t = 50/17.
综上,当t = 15/4或t = 50/17时,以点P、B、Q为顶点的三角形与△ABC相似.
(3)存在.
如图,过P作PE⊥BC,垂足为E,作△ABC的BC边上的高AD,

∵AB = AC = 10,BC = 12,
∴BD = CD = 1/2BC = 6,
∴AD = √(AB² - BD²) = 8,
∵∠BEP = ∠ADB = 90°,∠B = ∠B,
∴△PBE∽△ABD,
∴BP/AB = PE/AD,即(10 - t)/10 = PE/8,
∴PE = 8 - 4t/5,
∴S△PCQ = 1/2×CQ×PE = 1/2×(12 - 2t)×(8 - 4t/5) = 4,
解得t = 5或t = 11,
当t = 5时,经检验符合题意,
当t = 11时,BQ = 22>BC,故不合题意,
∴t = 5.
查看更多完整答案,请扫码查看


