《2025年5年中考3年模拟九年级数学下册人教版》

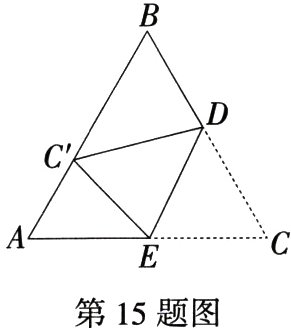
15.新独家原创如图,等边三角形ABC的边长为6,点D,E分别是BC,AC上的点,将△ABC沿DE折叠,使点C落在边AB上的C'处,若点C'是线段AB的三等分点,则线段BD的长为________.

答案： 答案　2.5或3.2
解析
∵等边三角形ABC的边长为6，
∴AB=BC=AC=6，∠A=∠B=∠C=60°，
∴∠AC'E+∠AEC'=120°.由折叠的性质可知，∠DC'E=∠C=60°，
∴∠AC'E+∠BC'D=120°，
∴∠BC'D=∠AEC'，
∴△AEC'∽△BC'D，
∴$\frac{BC'}{AE}$=$\frac{BD}{AC'}$=$\frac{C'D}{EC'}$.设BD=x，AE=y，则C'D=CD=6−x，C'E=CE=6−y，
∵点C'是线段AB的三等分点，
∴分两种情况:当AC'=2时，BC'=4，则$\frac{4}{y}$=$\frac{x}{2}$=$\frac{6−x}{6−y}$，解得x=2.5.当AC'=4时，BC'=2，则$\frac{2}{y}$=$\frac{x}{4}$=$\frac{6−x}{6−y}$，解得x=3.2.综上，BD的长为2.5或3.2.

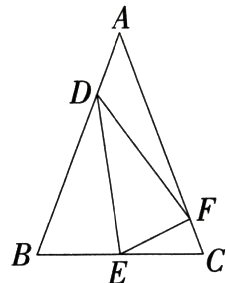
16.(2024江苏苏州姑苏月考)如图,在△ABC中,AB = AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF = ∠B,且点D,F分别在边AB,AC上.(M9227004)
(1)求证:$\frac{BE}{CF}=\frac{DE}{EF}$.
(2)当点E移动到BC的中点时,求证:FE平分∠DFC.

答案： 证明　
(1)
∵AB=AC，
∴∠B=∠C，
∵∠BDE=180°−∠B−∠DEB，∠CEF=180°−∠DEF−∠DEB，∠DEF=∠B，
∴∠BDE=∠CEF，
∴△BDE∽△CEF，
∴$\frac{BE}{CF}$=$\frac{DE}{EF}$.
(2)
∵点E是BC的中点，
∴BE=CE，
∵$\frac{BE}{CF}$=$\frac{DE}{EF}$，
∴$\frac{CE}{CF}$=$\frac{DE}{EF}$，
∴$\frac{CE}{DE}$=$\frac{CF}{EF}$，又∠DEF=∠B=∠C，
∴△DEF∽△ECF，
∴∠DFE=∠CFE，
∴FE平分∠DFC.

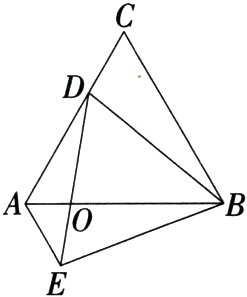
17.如图,△ABC和△BDE都是等边三角形,点D是AC上的点,连接AE,下列结论正确的有(M9227004) ( )
①△BCD∽△BEO;
②△AOD∽△EOB;
③△AOE∽△DOB;
④△BOD∽△BDA.

A.1个
B.2个
C.3个
D.4个

答案： △ABC和△BDE都是等边三角形，且共顶点，由手拉手相似模型可得△BCD∽△BAE，
∴∠CBD=∠ABE，∠OAE=∠DCB=60°，
∵∠C=∠BEO=60°，∠CBD=∠ABE，
∴△BCD∽△BEO，故①正确;
∵∠AOD=∠BOE，∠DAB=∠DEB=60°，
∴△AOD ∽△EOB，故②正确;
∵∠OAE=60°=∠BDE，∠AOE=∠DOB，
∴△AOE∽△DOB，故③正确;
∵∠DBA=∠DBO，∠DAB=60°=∠ODB，
∴△BOD∽△BDA，故④正确.所以，结论正确的有4个.故选D.

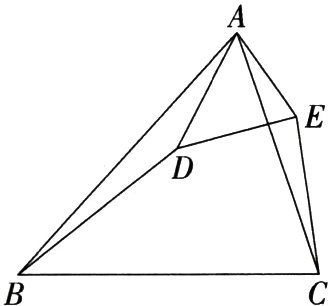
18.(2023四川遂宁射洪一中期中)如图,在△ABC和△ADE中,∠BAD = ∠CAE,∠ABD = ∠ACE.
求证:
(1)AB·AE = AC·AD.
(2)△ABC∽△ADE.

答案： 证明　
(1)
∵∠BAD=∠CAE，∠ABD=∠ACE，
∴△ABD∽△ACE，
∴$\frac{AB}{AC}$=$\frac{AD}{AE}$，
∴AB·AE=AC·AD.
(2)
∵∠BAD=∠CAE，
∴∠BAD+∠DAC=∠DAC+∠CAE，
即∠BAC=∠DAE，
∵$\frac{AB}{AC}$=$\frac{AD}{AE}$，
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$，
∴△ABC∽△ADE.

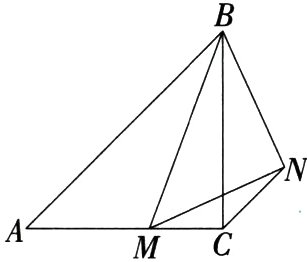
19.新考法(2024江苏连云港期中改编)如图,在Rt△ABC中,∠ACB = 90°,其中∠A = 45°,AC = 4,若点M是AC边上的动点,连接BM,以BM为斜边作等腰直角△BMN,连接CN.
(1)求证:AM = $\sqrt{2}$CN.
(2)求△CMN面积的最大值.

答案：
解析　
(1)证明:在Rt△ABC中，∠ACB=90°，∠A=45°，
∴△ABC是等腰直角三角形，
∴AB=$\sqrt{2}$BC，∠ABC=45°，
∵△BMN是等腰直角三角形，
∴BM=$\sqrt{2}$BN，∠MBN=45°=∠ABC，
∴∠ABM=∠CBN，又
∵$\frac{AB}{BC}$=$\frac{BM}{BN}$=$\sqrt{2}$，
∴△ABM∽△CBN，
∴$\frac{AM}{CN}$=$\sqrt{2}$，即AM=$\sqrt{2}$CN.
(2)如图，过点N作NH⊥AC，交AC的延长线于H，
∵△ABM∽△CBN，
∴∠BCN=∠BAC=45°，
∴∠ACN=135°，
∴∠NCH=45°，
∴NH=$\frac{\sqrt{2}}{2}$CN=$\frac{1}{2}$AM，
∴△CMN面积=$\frac{1}{2}$CM·NH=$\frac{1}{2}$CM·$\frac{1}{2}$(4 - CM)= - $\frac{1}{4}$(CM - 2)²+1，
∴当CM=2时，△CMN面积取最大值1，
∴△CMN面积的最大值为1.