《2025年5年中考3年模拟九年级数学下册人教版》

1.（2023江西抚州金溪模拟）如图，AG：GD = 4：1，BD：DC = 2：3，则AE：EC的值是（ ）

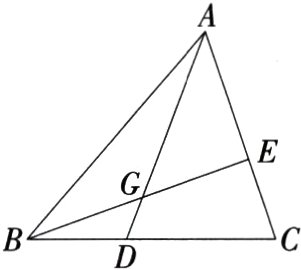
A.$\frac{8}{5}$
B.$\frac{4}{3}$
C.$\frac{3}{2}$
D.$\frac{6}{5}$

答案： 过D作DH//AC交BE于H，则△DHG∽△AEG，△BDH∽△BCE，
∴$\frac{DH}{AE}=\frac{DG}{AG}=\frac{1}{4}$，$\frac{DH}{CE}=\frac{BD}{BC}=\frac{2}{5}$，
∴$AE = 4DH$，$CE=\frac{5}{2}DH$，
∴$\frac{AE}{EC}=\frac{4DH}{\frac{5}{2}DH}=\frac{8}{5}$. 故选A.

2.（2024陕西商洛商南期末）如图，在△ABC中，F为AC的中点，过点F作EF⊥AB于点E，交BC的延长线于点D，若EF = 3，AB = 14，$\frac{BC}{CD}=\frac{3}{2}$，则BC的长为_______.

答案： 答案 $6\sqrt{2}$
解析 过点C作CM//EF交BE于M，
∵F为AC的中点，
∴E为AM的中点，
∴$CM = 2EF = 6$，
∵CM//ED，
∴△BCM∽△BDE，
∴$\frac{BC}{BD}=\frac{CM}{DE}=\frac{BM}{BE}=\frac{3}{5}$，
∴$DE=\frac{5}{3}\times6 = 10$，设$BM = 3x$，则$ME = 2x$，$AE = 2x$，
∴$3x + 2x + 2x = 14$，
∴$x = 2$，
∴$BE = 10$，
∴$BD=\sqrt{BE^{2}+ED^{2}} = 10\sqrt{2}$，
∴$BC=\frac{3}{5}BD=\frac{3}{5}\times10\sqrt{2}=6\sqrt{2}$.

3.（2024江苏无锡新吴期中）如图所示，△ABC中，D、E分别为BC、AB上的点，且AB = 3BE，$S_{\triangle ABD}=S_{\triangle ADC}$，若△ABC面积为30，则四边形ODBE的面积为_______.

答案： 答案 7
解析 如图，过E作EF//CD交AD于F，连接DE，
∵△ABC面积为30，$AB = 3BE$，
∴$S_{\triangle BEC}=10$，
∵$S_{\triangle ABD}=S_{\triangle ADC}$，
∴$BD = CD$，
∴$S_{\triangle BED}=S_{\triangle EDC}=5$，
∵EF//CD，
∴△AEF∽△ABD，△EFO∽△CDO，又$AB = 3BE$，$BD = CD$，
∴$\frac{EF}{BD}=\frac{AE}{AB}=\frac{2}{3}$，$\frac{EO}{OC}=\frac{EF}{CD}=\frac{EF}{BD}=\frac{2}{3}$，
∴$S_{\triangle EOD}=\frac{2}{5}S_{\triangle EDC}=\frac{2}{5}\times5 = 2$，
∴四边形ODBE的面积=$S_{\triangle BED}+S_{\triangle EOD}=5 + 2 = 7$.

4.（2024山西阳泉盂县二模）如图，在锐角△ABC中，AC = 3，AB = 4，∠ABC = 45°，BE是△ABC的中线，点F在BE上，延长AF交BC于点D.若BF = 3FE，则CD = _______.

答案： 答案 $\frac{4\sqrt{2}+2}{5}$
解析 如图，过点A作AH⊥BC于点H，
∵∠ABC = 45°，
∴△AHB是等腰直角三角形，
∴$AH = BH=\frac{\sqrt{2}}{2}AB=\frac{\sqrt{2}}{2}\times4 = 2\sqrt{2}$，在Rt△AHC中，由勾股定理，得$CH=\sqrt{AC^{2}-AH^{2}}=\sqrt{3^{2}-(2\sqrt{2})^{2}} = 1$，
∴$BC = BH + CH=2\sqrt{2}+1$，
∵BE是△ABC的中线，
∴点E是AC的中点，
∴$\frac{AE}{AC}=\frac{1}{2}$，过点E作EG//BC交AD于点G，则△AGE∽△ADC，
∴$\frac{GE}{DC}=\frac{AE}{AC}=\frac{1}{2}$，
∴$DC = 2GE$，
∵$BF = 3FE$，
∴$\frac{EF}{BF}=\frac{1}{3}$，
∵GE//BD，
∴△GFE∽△DFB，
∴$\frac{GE}{DB}=\frac{EF}{BF}=\frac{1}{3}$，
∴$\frac{DC}{DB}=\frac{2}{3}$，设$CD = 2a$，则$BD = 3a$，
∵$CD + BD = BC$，
∴$2a + 3a = 2\sqrt{2}+1$，
∴$a=\frac{2\sqrt{2}+1}{5}$，
∴$CD=\frac{4\sqrt{2}+2}{5}$.

5.（2024广东深圳模拟）在Rt△ABC中，∠ABC = 90°，AB = 3，BC = 4，点D在边AC上，CD = $\frac{8}{3}$，连接BD，过点A作AE⊥BD于点E，且AE的延长线交BC边于点F，则BF = _______.

答案： 答案 $\frac{18}{7}$
解析 作AG//CB交BD的延长线于点G，∠ABC = 90°，$AB = 3$，$BC = 4$，
∴$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}} = 5$，又$CD=\frac{8}{3}$，
∴$AD = AC - CD=5-\frac{8}{3}=\frac{7}{3}$，
∵AG//CB，
∴△AGD∽△CBD，
∴$\frac{GA}{BC}=\frac{AD}{CD}=\frac{\frac{7}{3}}{\frac{8}{3}}=\frac{7}{8}$，
∴$GA=\frac{7}{8}BC=\frac{7}{8}\times4=\frac{7}{2}$，
∵∠GAB = 180° - ∠ABC = 90°，
∴∠ABF = ∠GAB，
∵AE⊥BD，
∴∠AEB = 90°，
∴∠BAF + ∠ABG = 90°，又∠G + ∠ABG = 90°，
∴∠BAF = ∠G，
∴△ABF∽△GAB，
∴$\frac{BF}{AB}=\frac{AB}{GA}$，
∴$BF=\frac{AB^{2}}{GA}=\frac{3^{2}}{\frac{7}{2}}=\frac{18}{7}$.

6.（2024安徽合肥庐江月考）如图，在△ABC中，点D，E分别在边AB，AC上，ED、CB的延长线相交于点F.
（1）如图1，若∠AEF = ∠ABC，BF = 4，FD = 5，FE = 8，求FC的长.
（2）如图2，若$\frac{AB}{AC}=\frac{EF}{DF}$，求证：BD = CE.

答案： 解析 （1）
∵∠AEF = ∠ABC，
∴∠FBD = ∠FEC，又
∵∠F = ∠F，
∴△FBD∽△FEC，
∴$\frac{FB}{FE}=\frac{FD}{FC}$，
∵$BF = 4$，$FD = 5$，$FE = 8$，
∴$\frac{4}{8}=\frac{5}{FC}$，
∴$FC = 10$.
（2）证明：如图，过D作DH//AC交BC于H，
∴△BDH∽△BAC，△FDH∽△FEC，
∴$\frac{AB}{AC}=\frac{BD}{DH}$，$\frac{EF}{DF}=\frac{CE}{DH}$，
∵$\frac{AB}{AC}=\frac{EF}{DF}$，
∴$\frac{BD}{DH}=\frac{CE}{DH}$，
∴$BD = CE$.