《2025年5年中考3年模拟九年级数学下册人教版》

1.(2023山东泰安东平二模)某驱逐舰在海上执行任务后刚返回到港口A，就接到上级指令，发现在其北偏东30°方向上有一艘可疑船只C，与此同时在港口A北偏东60°方向上10 km处有另一艘驱逐舰B也收到了相关指令，驱逐舰B恰好在可疑船只C的南偏东30°方向上，则可疑船只C与港口A之间的距离为(M9228005) （ ）
A.$\frac{5\sqrt{3}}{3}$ km B.$\frac{10\sqrt{3}}{3}$ km C.$\frac{20\sqrt{3}}{3}$ km D.10$\sqrt{3}$ km
　　　　　　　　　　　

答案： C
∵可疑船只C在港口A北偏东30°方向上，驱逐舰B在港口A北偏东60°方向上，
∴∠CAB = 60° - 30° = 30°，
∵驱逐舰B在可疑船只C的南偏东30°方向上，
∴∠ACB = 30° + 30° = 60°，
∴∠ABC = 180° - 30° - 60° = 90°，
∴sin∠ACB = $\frac{AB}{AC}$，
∵AB = 10 km，
∴AC = $\frac{AB}{\sin∠ACB}=\frac{10}{\sin 60^{\circ}}=\frac{20\sqrt{3}}{3}$（km）. 故选C.

2.(2024浙江台州仙居三模)图1是一盏悬挂灯的图片，图2是悬挂灯的示意图，连接管ED所在的直线和固定管AB所在的直线都经过圆心O，AB⊥BD.测得∠BDE = 140°，BD = 10 cm，AB = 1 cm，求⊙O的半径.（精确到0.1 cm.参考数据：sin 40°≈0.643，cos 40°≈0.766，tan 40°≈0.839）(M9228005)
　　　　　　　

答案： 解析 在Rt△DBO中，∠DBO = 90°，tan∠BDO = $\frac{BO}{BD}$，
∵∠BDO = 180° - ∠BDE = 40°，
∴BO = BD·tan∠BDO = 10×tan 40°≈8.39.
∴OA = BO - AB = 8.39 - 1 = 7.39≈7.4.
∴⊙O的半径约为7.4 cm.

3.(2024四川德阳中江一模)如图，在湖边高出水面50 m的山顶A处看见一架无人机停留在湖面上空某处，观察到无人机底部标志P处的仰角为45°，又观其在湖中之像P'(P与P'到湖面的距离相等)的俯角为60°，则无人机距湖面的高度为 （ ）
　　　　　　　　
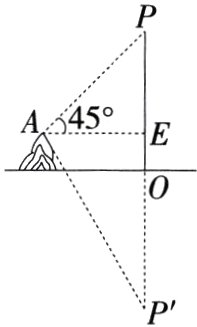
A.(25$\sqrt{3}$+75)m
B.(50$\sqrt{3}$+50)m
C.(75$\sqrt{3}$+75)m
D.(50$\sqrt{3}$+100)m

答案： D 设AE = x m，在Rt△AEP中，∠PAE = 45°，则∠P = 45°，
∴PE = AE = x m，
∵山顶A处高出水面50 m，
∴OE = 50 m，
∴OP' = OP = PE + OE = (x + 50) m，
∵∠P'AE = 60°，
∴P'E = tan 60°·AE = $\sqrt{3}x$ m，
∴OP' = P'E - OE = ($\sqrt{3}x - 50$) m，
∴x + 50 = $\sqrt{3}x - 50$，解得x = 50$\sqrt{3}$ + 50，
∴PO = PE + OE = 50$\sqrt{3}$ + 50 + 50 = (50$\sqrt{3}$ + 100) m，即无人机距湖面的高度是(50$\sqrt{3}$ + 100) m. 故选D.

4.(2023山东菏泽中考)无人机在实际生活中的应用越来越广泛.如图所示，某人利用无人机测量大楼的高度BC，无人机在空中点P处，测得点P距地面上的点A 80米，点A处的俯角为60°，楼顶点C处的俯角为30°，已知点A与大楼的距离AB为70米（点A，B，C，P在同一平面内），求大楼的高度BC（结果保留根号）.
　　　　　　　　　　　

答案：
解析 如图所示，过P作PH⊥AB于H，过C作CQ⊥PH于Q，又CB⊥AB，则四边形CQHB是矩形，
∴QH = BC，BH = CQ. 由题意可得AP = 80，∠PAH = ∠1 = 60°，∠PCQ = ∠2 = 30°，AB = 70，
∴PH = AP·sin 60° = 80×$\frac{\sqrt{3}}{2}$ = 40$\sqrt{3}$，AH = AP·cos 60° = 40，
∴CQ = BH = AB - AH = 70 - 40 = 30，
∴PQ = CQ·tan 30° = 10$\sqrt{3}$，
∴BC = QH = PH - PQ = 40$\sqrt{3}$ - 10$\sqrt{3}$ = 30$\sqrt{3}$，
∴大楼的高度BC为30$\sqrt{3}$米.