《2025年5年中考3年模拟九年级数学下册人教版》

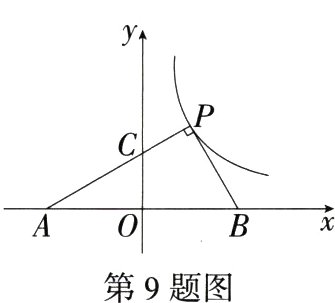
9.(2024广东梅州五华模拟)如图，在平面直角坐标系中，点P在反比例函数y = $\frac{k}{x}$(x＞0)的图象上，点A，B在x轴上，且PA⊥PB，垂足为P，PA交y轴于点C，AO = BO = BP，△ABP的面积是2，则k的值是 ( )

A.1
B.$\frac{3}{2}$
C.$\sqrt{3}$
D.2

答案：
9A 如图，连接OP，作PD⊥x轴于D，
∵△ABP的面积是2，AO = BO，
∴△OBP的面积为1，
∵PA⊥PB，AO = BO = BP，
∴sin∠PAB = $\frac{1}{2}$，
∴∠PAB = 30°，
∴∠PBA = 60°，
∴△POB为等边三角形，
∴S△POD = $\frac{1}{2}$S△POB = $\frac{1}{2}$，
∴$\frac{|k|}{2}$ = $\frac{1}{2}$，
∴k = ±1，
∵反比例函数的图象位于第一象限，
∴k = 1.故选A.

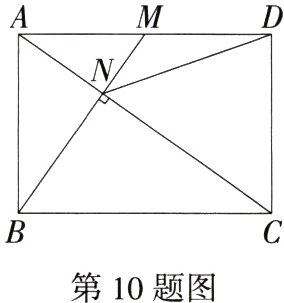
10.(2024甘肃武威凉州一模)如图，已知在矩形ABCD中，M是AD边的中点，BM与AC垂直，交直线AC于点N，连接DN，则下列四个结论：①CN = 2AN；②DN = DC；③tan∠CAD = $\sqrt{2}$；④△AMN∽△CAB.其中，正确的为 ( )

A.①②③④
B.①②③
C.①②④
D.②③④

答案：
10C
∵矩形ABCD中，AD//BC，
∴△AMN∽△CBN，
∴$\frac{AM}{BC}$ = $\frac{AN}{CN}$，
∵M是AD边的中点，
∴AM = MD = $\frac{1}{2}$AD = $\frac{1}{2}$BC，
∴$\frac{AM}{BC}$ = $\frac{AN}{CN}$ = $\frac{1}{2}$，
∴CN = 2AN，故①正确；如图，过D作DH//BM交BC于H，连接NH，
∵DH//BM，BM⊥AC，
∴DH⊥AC，
∵DH//BM，AD//BC，
∴四边形BMDH是平行四边形，
∴BH = MD = $\frac{1}{2}$BC，
∴BH = CH，
∵∠BNC = 90°，
∴NH = HC，
∴DH是NC的垂直平分线，
∴DN = DC，故②正确；
∵四边形ABCD是矩形，
∴AD//BC，∠ABC = 90°，
∴∠DAC = ∠ACB，∠ABC = ∠ANM = 90°，
∴△AMN∽△CAB，故④正确；
∵∠DAC = ∠BCA，∠BAC + ∠ACB = 90°，∠DAC + ∠AMB = 90°，
∴∠BAC = ∠AMB，
∵∠ABC = ∠BAM = 90°，
∴△ABM∽△BCA，
∴$\frac{AM}{AB}$ = $\frac{AB}{BC}$，
∴AB² = $\frac{1}{2}$BC²，
∴AB = $\frac{\sqrt{2}}{2}$BC，
∵tan∠DAC = tan∠ACB = $\frac{AB}{BC}$，
∴tan∠DAC = $\frac{\sqrt{2}}{2}$，故③错误.故选C.

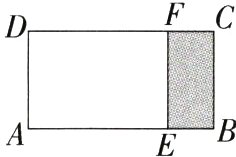
11.(2023浙江金华武义模拟)如图，矩形ABCD中，AD = 2，AB = 4，剪去一个矩形AEFD后，余下的矩形EBCF∽矩形BCDA，则CF的长为________.(M9227002)

答案： 11答案 1
解析
∵四边形ABCD是矩形，
∴AD = BC = 2，AB = DC = 4，
∵矩形EBCF∽矩形BCDA，
∴$\frac{BC}{CD}$ = $\frac{CF}{AD}$，即$\frac{2}{4}$ = $\frac{CF}{2}$，
∴CF = 1.

12.(新独家原创)定义一种运算：$\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad - bc$.例如：$\begin{vmatrix}1&2\\-3&4\end{vmatrix}=1×4 - 2×(-3)=10$，则$\begin{vmatrix}\sin60°&\cos45°\\\tan30°&\sqrt{2}\end{vmatrix}$的值为________.

答案： 12答案 $\frac{\sqrt{6}}{3}$
解析 $\begin{vmatrix}\sin 60^{\circ}&\cos 45^{\circ}\\\tan 30^{\circ}&\sqrt{2}\end{vmatrix}$ = sin 60°×$\sqrt{2}$ - cos 45°·tan 30° = $\frac{\sqrt{3}}{2}$×$\sqrt{2}$ - $\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{3}$ = $\frac{\sqrt{6}}{2}$ - $\frac{\sqrt{6}}{6}$ = $\frac{\sqrt{6}}{3}$.

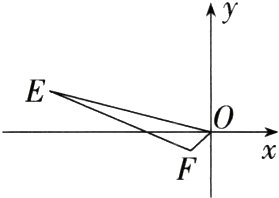
13.(易错题)(2023辽宁抚顺东洲模拟)如图，已知点E(-6,2)，F(-1,-1)，以点O为位似中心，把△EFO各边缩小到原来的$\frac{1}{2}$，则点E的对应点的坐标为________________.(M9227006)

答案： 13答案 （-3，1）或（3，-1）
解析
∵以点O为位似中心，把△EFO各边缩小到原来的$\frac{1}{2}$，点E的坐标为（-6，2），
∴点E的对应点的坐标为（-6×$\frac{1}{2}$，2×$\frac{1}{2}$）或（-6×（-$\frac{1}{2}$），2×（-$\frac{1}{2}$）），即（-3，1）或（3，-1）.
易错点 易忽略其中一种情况.

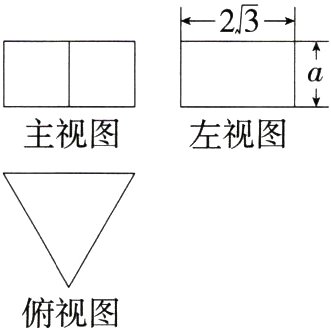
14.(2024浙江宁波一模)一个正三棱柱的三视图如图所示，若这个正三棱柱的表面积为24 + 8$\sqrt{3}$，则a的值是________.

答案： 14答案 2
解析 由左视图知底面正三角形的高为2$\sqrt{3}$，可得底面正三角形的边长为4，
∴底面正三角形的面积为$\frac{1}{2}$×4×2$\sqrt{3}$ = 4$\sqrt{3}$，
∵这个正三棱柱的表面积为24 + 8$\sqrt{3}$，
∴3×4a + 2×4$\sqrt{3}$ = 24 + 8$\sqrt{3}$，
∴a = 2.

15.(2024湖南中考)如图，左图为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”的结构简图，右图为其平面示意图.已知AB⊥CD于点B，AB与水平线l相交于点O，OE⊥l.若BC = 4分米，OB = 12分米，∠BOE = 60°，则点C到水平线l的距离CF为________分米(结果用含根号的式子表示).

答案：
15答案 （6 - 2$\sqrt{3}$）
解析 如图，延长DC交l于点H，连接OC，在Rt△OBH中，∠BOH = 90° - 60° = 30°，OB = 12分米，
∴BH = 12×tan 30° = 4$\sqrt{3}$（分米），OH = 8$\sqrt{3}$分米，
∵S△OBH = S△OCH + S△OBC，
∴$\frac{1}{2}$OB·BH = $\frac{1}{2}$OH·CF + $\frac{1}{2}$OB·BC，即$\frac{1}{2}$×12×4$\sqrt{3}$ = $\frac{1}{2}$×8$\sqrt{3}$×CF + $\frac{1}{2}$×12×4，
∴CF = （6 - 2$\sqrt{3}$）分米.

16.(2024四川广元旺苍三模)如图，一次函数y₁ = ax + b与反比例函数y₂ = $\frac{4}{x}$的图象交于A、B两点，点A的横坐标为2，点B的纵坐标为1，在反比例函数y₂ = $\frac{4}{x}$位于第三象限的图象上存在一点P，要使点P到直线AB的距离最短，则点P的坐标为________.

答案： 16答案 （-2$\sqrt{2}$，-$\sqrt{2}$）
解析
∵点A、B在反比例函数y₂ = $\frac{4}{x}$的图象上，且点A的横坐标为2，点B的纵坐标为1，
∴A（2，2），B（4，1）.
∵A（2，2），B（4，1）在一次函数y₁ = ax + b的图象上，
∴$\begin{cases}2a + b = 2\\4a + b = 1\end{cases}$，解得$\begin{cases}a = -\frac{1}{2}\\b = 3\end{cases}$，
∴直线AB的解析式为y₁ = -$\frac{1}{2}$x + 3.设直线AB向下平移m个单位时，其与反比例函数在第三象限内的图象只有一个交点，交点为点P，此时点P到直线AB的距离最短，令-$\frac{1}{2}$x + 3 - m = $\frac{4}{x}$，整理得x² - 2（3 - m）x + 8 = 0，令Δ = 4（3 - m）² - 32 = 0，解得m = 3 + 2$\sqrt{2}$或m = 3 - 2$\sqrt{2}$（舍去），此时x² - 2（3 - m）x + 8 = 0整理为x² + 4$\sqrt{2}$x + 8 = 0，解得x₁ = x₂ = -2$\sqrt{2}$，
∴满足条件的点P的坐标为（-2$\sqrt{2}$，-$\sqrt{2}$）.