《2025年5年中考3年模拟九年级数学下册人教版》

7.(2024黑龙江绥化肇东模拟）如图，在Rt△ABC中，∠C = 90°，AC = 9，BC = 4，以点C为圆心，3为半径作⊙C，分别交AC，BC于D，E两点，点P是⊙C上一个动点，则$\frac{1}{3}$PA + PB的最小值为________.
　　　

答案：
答案 $\sqrt{17}$
解析 如图,在AC上截取CQ = 1,连接CP,PQ,BQ。
∵AC = 9,CP = 3,
∴$\frac{CP}{AC}$=$\frac{1}{3}$,
∵CP = 3,CQ = 1,
∴$\frac{CQ}{CP}$=$\frac{1}{3}$,
∴△ACP∽△PCQ,
∴PQ =$\frac{1}{3}$AP,
∴$\frac{1}{3}$PA+PB = PQ+PB≥BQ。在Rt△BCQ中,BC = 4,CQ = 1,
∴QB =$\sqrt{17}$,
∴$\frac{1}{3}$PA+PB的最小值为$\sqrt{17}$。

8.如图，四边形ABCD是边长为4的正方形，⊙B的半径为2，P是⊙B上一动点，则PD + $\frac{1}{2}$PC的最小值为________.
　　　

答案：
答案 5
解析 如图,连接PB,在BC上取一点E,使得BE = 1,连接PE,DE。
∵PB = 2,BC = 4,
∴$\frac{BE}{PB}$=$\frac{PB}{BC}$。
∵∠PBE = ∠CBP,
∴△PBE∽△CBP,
∴$\frac{PE}{PC}$=$\frac{PB}{BC}$=$\frac{1}{2}$,
∴PE =$\frac{1}{2}$PC,
∴PD+$\frac{1}{2}$PC = PD+PE。
∵PE+PD≥DE,在Rt△DCE中,DE =$\sqrt{3^{2}+4^{2}}$= 5,
∴PD+$\frac{1}{2}$PC的最小值为5。

9.如图，在边长为6的正方形ABCD中，M为AB上一点，且BM = 2，N为边BC上一动点，连接MN.点B关于MN的对称点为P，连接PA，PC，则PA + 2PC的最小值为________.
　　　　　　　

答案：
答案 6$\sqrt{5}$
解析 由对称得MP = BM = 2,则点P在以M为圆心,BM的长为半径的圆弧上运动。如图,在AM上取一点E,使EM =$\frac{1}{2}$MP = 1,连接EP,EC。

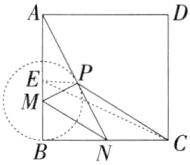
∵AB = 6,BM = 2,
∴AM = 4,EB = 3。
∵$\frac{PM}{AM}$=$\frac{1}{2}$=$\frac{EM}{PM}$,∠PME = ∠AMP,
∴△PME∽△AMP,
∴EP =$\frac{1}{2}$PA,
∴PC+$\frac{1}{2}$PA = PC+EP。当C,P,E三点共线时,PC+$\frac{1}{2}$PA取最小值,最小值为EC的长。在Rt△EBC中,由勾股定理得EC =$\sqrt{EB^{2}+BC^{2}}$=$\sqrt{3^{2}+6^{2}}$= 3$\sqrt{5}$。
∵PA+2PC = 2($\frac{1}{2}$PA+PC),
∴PA+2PC的最小值为6$\sqrt{5}$。