《2025年5年中考3年模拟九年级数学下册人教版》

1.(2022福建中考)如图所示的衣架可以近似看成一个等腰三角形ABC，其中AB =AC，∠ABC = 27°，BC = 44 cm，则高AD约为（参考数据：sin 27°≈0.45，cos 27°≈0.89，tan 27°≈0.51）（ ）

A.9.90 cm
B.11.22 cm
C.19.58 cm
D.22.44 cm

答案： B
∵AB = AC，BC = 44 cm，AD⊥BC，
∴BD = CD = 22 cm.
∵∠ABC = 27°，
∴tan∠ABC = $\frac{AD}{BD}$≈0.51，
∴AD≈0.51×22 = 11.22 cm.
故选B.

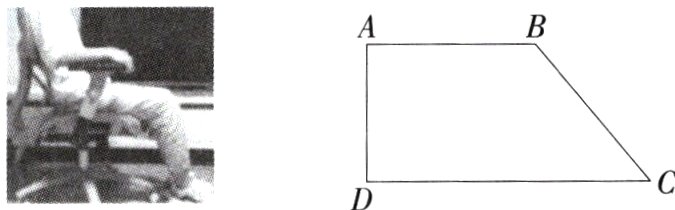
2.(情境题·现实生活)(2024广东深圳福田三模)人体工学椅提出正确的座垫高度须将座垫高度调整到人的双脚能平放于地面，且大腿与小腿之间的弯曲角度呈现90°的位置.如图所示的是一男士坐在椅子上的情况的示意图，若椅子座垫高度AD = 40 cm，男士的小腿与地面的夹角∠C = 50°，则椅子座垫还要升高多少厘米，才符合人体工学椅的要求（ ）

A.40sin 50° - 40
B.40cos 50° - 40
C.$\frac{40}{\sin 50^{\circ}} - 40$
D.$\frac{40}{\cos 50^{\circ}} - 40$

答案：
C 如图，过点B作BE⊥CD，垂足为E，由题意得AD = BE = 40 cm，在Rt△BCE中，∠C = 50°，
∴BC = $\frac{BE}{\sin 50^{\circ}}=\frac{40}{\sin 50^{\circ}}$cm，
∴该椅子座垫还要升高的高度 = BC - BE = $(\frac{40}{\sin 50^{\circ}} - 40)$cm.
故选C.

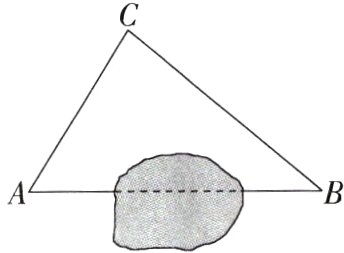
3.(2023内蒙古赤峰中考)为发展城乡经济，建设美丽乡村，某乡村对A地和B地之间的一处垃圾填埋场进行改造，把原来A地去往B地需要绕行到C地的路线，改造成可以直线通行的公路AB.如图，经测量，AC = 6千米，∠CAB = 60°，∠CBA = 37°，则改造后的公路AB的长是________千米（精确到0.1千米；参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75，$\sqrt{3}$≈1.73）.

答案：
答案 9.9
解析 如图，过点C作CD⊥AB于点D，在Rt△ADC中，AC = 6千米，∠CAD = 60°，cos∠CAD = $\frac{AD}{AC}$，sin∠CAD = $\frac{CD}{AC}$，
∴AD = AC·cos∠CAD = 6cos 60° = 3(千米)，CD = AC·sin∠CAD = 6sin 60° = $3\sqrt{3}$(千米).在Rt△CDB中，∠CBD = 37°，CD = $3\sqrt{3}$千米，tan∠CBD = $\frac{CD}{DB}$，
∴DB = $\frac{CD}{\tan\angle CBD}=\frac{3\sqrt{3}}{\tan 37^{\circ}}\approx\frac{3\sqrt{3}}{0.75}=4\sqrt{3}$(千米)，
∴AB = AD + DB = 3 + $4\sqrt{3}$≈3 + 4×1.73≈9.9(千米)，即改造后的公路AB的长约是9.9千米.

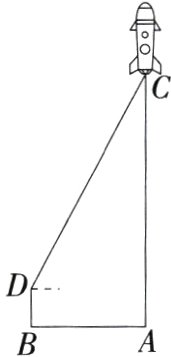
4.(2024广东深圳罗湖模拟)某校化学实验小组利用白醋和小苏打自制火箭发射小实验.如图，一枚自制小火箭从发射点A处发射，身高为1.8米的小明在离发射点A 6米的B处，当小火箭到达C点时，小明测得此刻的仰角为62°，则这枚小火箭此时的高度AC为（ ）

A.(6tan 62° + 1.8)米
B.(6sin 62° + 1.8)米
C.(6cos 62° + 1.8)米
D.$(\frac{6}{\tan 62^{\circ}} + 1.8)$米

答案：
A 如图，过点D作DE⊥AC，垂足为E，由题意得，BD = AE = 1.8米，DE = AB = 6米，在Rt△CDE中，∠CDE = 62°，
∴CE = DE·tan 62° = 6tan 62°(米)，
∴AC = CE + AE = ($6\tan 62^{\circ}+1.8$)米.故选A.

5.(2024福建福州模拟)港珠澳大桥是世界上最长的跨海大桥，它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥，其中九洲航道桥主塔造型取自“风帆”，寓意“扬帆起航”，某校九年级学生为了测量该主塔的高度，站在B处看塔顶A，仰角为60°，然后向后走160米(BC = 160米)，到达C处，此时看塔顶A，仰角为30°，则该主塔的高度是________米.(M9228005)

答案：
答案 $80\sqrt{3}$
解析 如图，过点A作AD⊥直线CB，垂足为D，由题意得，∠ABD = 60°，∠ACD = 30°，
∵∠ABD是△ABC的一个外角，
∴∠CAB = ∠ABD - ∠ACD = 30°，
∴∠CAB = ∠ACD = 30°，
∴BA = BC = 160米，在Rt△ABD中，AD = AB·sin 60° = 160×$\frac{\sqrt{3}}{2}=80\sqrt{3}$(米)，
∴该主塔的高度是$80\sqrt{3}$米.