《2025年5年中考3年模拟九年级数学下册人教版》

17.[答案含评分细则](8分)(2022贵州贵阳中考)在初中阶段我们已经学习了一元二次方程的三种解法，它们分别是配方法、公式法和因式分解法，请从下列一元二次方程中任选两个，并解这两个方程.
①$x^{2}+2x - 1 = 0$；②$x^{2}-3x = 0$；③$x^{2}-4x = 4$；④$x^{2}-4 = 0$.

答案： 解析 ①利用公式法：$x^{2}+2x - 1 = 0$，$\Delta=2^{2}-4\times1\times(-1)=4 + 4 = 8$，$\therefore x=\frac{-2\pm\sqrt{8}}{2}=\frac{-2\pm2\sqrt{2}}{2}=-1\pm\sqrt{2}$. $\therefore x_{1}=-1+\sqrt{2}$，$x_{2}=-1-\sqrt{2}$.
②利用因式分解法：$x^{2}-3x = 0$，$\therefore x(x - 3)=0$. $\therefore x_{1}=0$，$x_{2}=3$.
③利用配方法：$x^{2}-4x = 4$，两边都加上4，得$x^{2}-4x + 4 = 8$，$\therefore(x - 2)^{2}=8$. $\therefore x - 2=\pm2\sqrt{2}$. $\therefore x_{1}=2+2\sqrt{2}$，$x_{2}=2-2\sqrt{2}$.
④利用因式分解法：$x^{2}-4 = 0$，$\therefore(x + 2)(x - 2)=0$. $\therefore x_{1}=-2$，$x_{2}=2$.
（注：任选两个即可，每个4分，共8分）

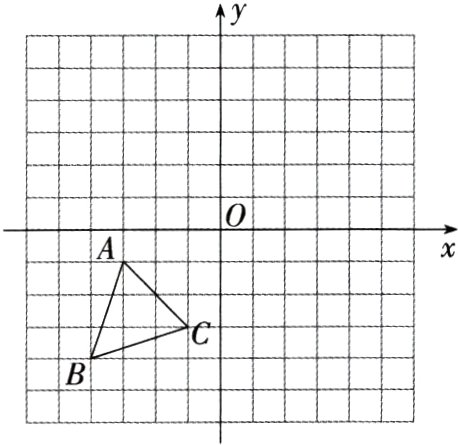
18.[答案含评分细则](10分)(2023安徽马鞍山和县二模)如图，在平面直角坐标系中，$\triangle ABC$三个顶点的坐标分别为$A(-3,-1)$，$B(-4,-4)$，$C(-1,-3)$.
(1)以点$O$为位似中心，在第一象限作出$\triangle ABC$的位似图形$\triangle A_{1}B_{1}C_{1}$，使$\triangle ABC$与$\triangle A_{1}B_{1}C_{1}$的相似比为$1:1$.
(2)以点$O$为旋转中心，将$\triangle ABC$顺时针旋转$90^{\circ}$后得$\triangle A_{2}B_{2}C_{2}$，请作出$\triangle A_{2}B_{2}C_{2}$.
(3)直接写出$\cos\angle BAC$的值.

答案：
解析 （1）如图，$\triangle A_{1}B_{1}C_{1}$即为所作. ………… 3分

（2）如图，$\triangle A_{2}B_{2}C_{2}$即为所作. ……………… 6分
（3）$\cos\angle BAC=\frac{\sqrt{5}}{5}$. ……………………… 10分
详解：$\because AB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$，$BC=\sqrt{1^{2}+3^{2}}=\sqrt{10}$，$\therefore AB = BC$. 如图，取$AC$的中点$D$，则$BD\perp AC$，在$Rt\triangle ABD$中，$\because AD=\sqrt{1^{2}+1^{2}}=\sqrt{2}$，$\therefore\cos\angle BAD=\frac{AD}{AB}=\frac{\sqrt{2}}{\sqrt{10}}=\frac{\sqrt{5}}{5}$.

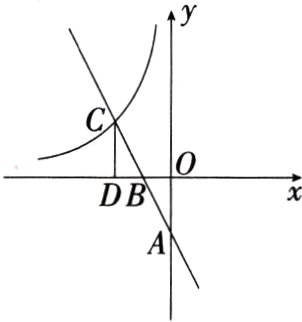
19.[答案含评分细则](10分)(2024四川南充中考)如图，直线$y = kx + b$经过$A(0,-2)$，$B(-1,0)$两点，与双曲线$y=\frac{m}{x}(x ＜ 0)$交于点$C(a,2)$.
(1)求直线和双曲线的解析式.
(2)过点$C$作$CD\perp x$轴于点$D$，点$P$在$x$轴上，若以$O$，$A$，$P$为顶点的三角形与$\triangle BCD$相似，直接写出点$P$的坐标.

答案： 解析 （1）$\because A(0,-2)$，$B(-1,0)$在直线$y = kx + b$上，$\therefore\begin{cases}b=-2\\-k + b = 0\end{cases}$，解得$\begin{cases}k=-2\\b=-2\end{cases}$，$\therefore$直线的解析式为$y=-2x - 2$. ……………… 2分
$\because C(a,2)$在直线$y=-2x - 2$上，$\therefore - 2a-2 = 2$，$\therefore a=-2$，即$C(-2,2)$. …………………… 3分
$\because$双曲线$y=\frac{m}{x}$经过$C(-2,2)$，$\therefore m=-4$，$\therefore$双曲线的解析式为$y=-\frac{4}{x}$. ……………… 4分
（2）点$P$的坐标为$(-4,0)$或$(-1,0)$或$(1,0)$或$(4,0)$.
详解：$\because CD\perp x$轴，$C(-2,2)$，$\therefore D(-2,0)$，$CD = 2$，$\because B(-1,0)$，$\therefore BD = 1$，$\because A(0,-2)$，$\therefore OA = 2$，$\because$以$O$，$A$，$P$为顶点的三角形与$\triangle BCD$相似，$\angle AOP = 90^{\circ}$，$\therefore OP = 1$或4，$\because$点$P$在$x$轴上，$\therefore$点$P$的坐标为$(-4,0)$或$(-1,0)$或$(1,0)$或$(4,0)$.

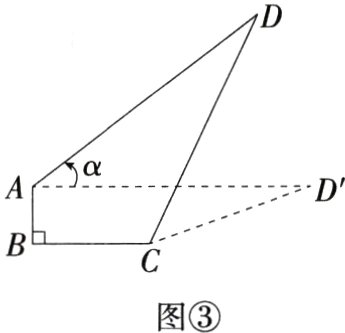
20.[答案含评分细则](12分)(2024江苏苏州中考)图①是某种可调节支撑架，$BC$为水平固定杆，竖直固定杆$AB\perp BC$，活动杆$AD$可绕点$A$旋转，$CD$为液压可伸缩支撑杆，已知$AB = 10$ cm，$BC = 20$ cm，$AD = 50$ cm.
(1)如图②，当活动杆$AD$处于水平状态时，求可伸缩支撑杆$CD$的长度(结果保留根号).
(2)如图③，当活动杆$AD$绕点$A$由水平状态逆时针旋转$\alpha$，且$\tan\alpha=\frac{3}{4}$($\alpha$为锐角)时，求可伸缩支撑杆$CD$的长度(结果保留根号).

答案：
解析 （1）如图1，过点$C$作$CE\perp AD$，垂足为$E$，由题意得$AB = CE = 10\ cm$，$BC = AE = 20\ cm$，$\because AD = 50\ cm$，$\therefore ED = AD - AE = 50 - 20 = 30(cm)$，在$Rt\triangle CED$中，$CD=\sqrt{CE^{2}+DE^{2}}=10\sqrt{10}\ cm$，$\therefore$可伸缩支撑杆$CD$的长度为$10\sqrt{10}\ cm$. …… 5分

（2）如图2，过点$D$作$DF\perp BC$，交$BC$的延长线于点$F$，交$AD'$于点$G$，由题意得$AB = FG = 10\ cm$，$AG = BF$，$\angle AGD = 90^{\circ}$，在$Rt\triangle ADG$中，$\tan\alpha=\frac{DG}{AG}=\frac{3}{4}$，设$DG = 3x\ cm$，则$AG = 4x\ cm$，$\therefore AD=\sqrt{AG^{2}+DG^{2}}=\sqrt{(4x)^{2}+(3x)^{2}} = 5x(cm)$，$\because AD = 50\ cm$，$\therefore 5x = 50$，解得$x = 10$，$\therefore AG = 40\ cm$，$DG = 30\ cm$，$\therefore DF = DG + FG = 30 + 10 = 40(cm)$，$BF = AG = 40\ cm$，$\because BC = 20\ cm$，$\therefore CF = BF - BC = 40 - 20 = 20(cm)$，在$Rt\triangle CFD$中，$CD=\sqrt{CF^{2}+DF^{2}}=20\sqrt{5}\ cm$，$\therefore$可伸缩支撑杆$CD$的长度为$20\sqrt{5}\ cm$. …… 12分