《2025年5年中考3年模拟九年级数学下册人教版》

9.新独家原创 若函数$y = mx^{m^{2}+m - 1}$是关于$x$的反比例函数,则$m^{2025}=$_______.

答案： 答案 -1
解析 $\because$函数$y = mx^{m^{2}+m - 1}$是关于$x$的反比例函数，$\therefore m^{2}+m - 1 = -1$且$m\neq0$，$\therefore m = -1$，则$m^{2025}=(-1)^{2025} = -1$.

10.新考向·开放型试题 (2024福建福州模拟)若反比例函数$y = \frac{k - 2}{x}$的图象位于第一、三象限,则$k$的值可以是(写出一个满足条件的$k$值即可)_______.(M9226003)

答案： 答案 3（答案不唯一，满足$k\gt2$即可）
解析 $\because$反比例函数$y=\frac{k - 2}{x}$的图象位于第一、第三象限，$\therefore k - 2\gt0$，即$k\gt2$，不妨取$k = 3$.

11.(2024山东济宁邹城模拟)反比例函数$y = \frac{3}{x}$图象上三个点的坐标为$(x_1,y_1)$、$(x_2,y_2)$、$(x_3,y_3)$,若$x_1 ＜ 0 ＜ x_2 ＜ x_3$,则$y_1$、$y_2$、$y_3$的大小关系是_______.

答案： 答案 $y_1\lt y_3\lt y_2$
解析 $\because k = 3\gt0$，$\therefore$反比例函数$y=\frac{3}{x}$的图象位于第一、三象限，且在每个象限内，$y$随$x$的增大而减小，$\because$反比例函数$y=\frac{3}{x}$图象上三个点的坐标为$(x_1,y_1)$、$(x_2,y_2)$、$(x_3,y_3)$，$x_1\lt0$，$x_2\gt0$，$x_3\gt0$，$\therefore (x_1,y_1)$位于第三象限，$(x_2,y_2)$、$(x_3,y_3)$位于第一象限，$\therefore y_1\lt0$，$y_2\gt0$，$y_3\gt0$，$\because x_2\lt x_3$，$\therefore y_3\lt y_2$，$\therefore y_1\lt0\lt y_3\lt y_2$，即$y_1\lt y_3\lt y_2$.

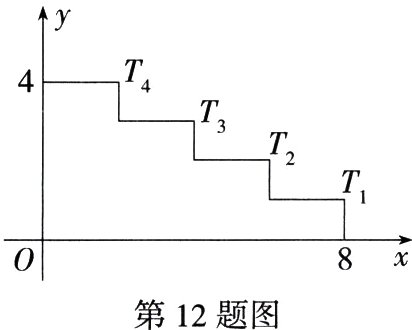
12.如图所示的是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作$T_m(m为1~4的整数)$,反比例函数$y = \frac{k}{x}(x ＞ 0)$的图象为曲线$L$.若曲线$L$使得$T_1~T_4$这些点分布在它的两侧,每侧各2个点,则$k$的取值范围是_______.
　

答案： 答案 $8\lt k\lt12$
解析 $\because$每个台阶的高和宽分别是 1 和 2，$\therefore T_1(8,1)$，$T_2(6,2)$，$T_3(4,3)$，$T_4(2,4)$，则$8\times1 = 2\times4$，$6\times2 = 4\times3$，当函数$y=\frac{k}{x}(x\gt0)$的图象过点$T_1(8,1)$，$T_4(2,4)$时，$k = 8$；当函数$y=\frac{k}{x}(x\gt0)$的图象过点$T_2(6,2)$，$T_3(4,3)$时，$k = 12$. 由此可知若曲线$L$使得$T_1～T_4$这些点分布在它的两侧，每侧各 2 个点，则$k$的取值范围是$8\lt k\lt12$.

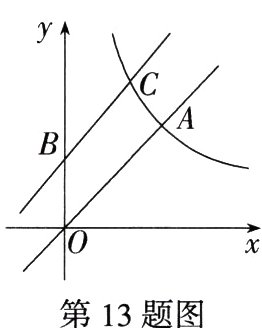
13.(2023湖北荆州中考)如图,点$A(2,2)$在反比例函数$y = \frac{k}{x}(x ＞ 0)$的图象上,将直线$OA$向上平移若干个单位长度交$y$轴于点$B$,交反比例函数图象于点$C$.若$BC = 2$,则点$C$的坐标是_______.
　　

答案： 答案 $(\sqrt{2},2\sqrt{2})$
解析 $\because$点$A(2,2)$在反比例函数$y=\frac{k}{x}(x\gt0)$的图象上，$\therefore 2=\frac{k}{2}$，$\therefore k = 4$，$\therefore$反比例函数解析式为$y=\frac{4}{x}(x\gt0)$. 如图，作$AD\perp x$轴，$CH\perp x$轴，$BG\perp CH$，垂足分别为$D$，$H$，$G$. $\because A(2,2)$，$\therefore AD = OD$，$\therefore \angle AOD = 45^{\circ}$，$\therefore \angle AOB = 45^{\circ}$. $\because OA// BC$，$\therefore \angle CBO = 180^{\circ}-45^{\circ}=135^{\circ}$，又易知$\angle OBG = 90^{\circ}$，$\therefore \angle CBG = 135^{\circ}-90^{\circ}=45^{\circ}$，$\therefore \angle CBG=\angle BCG = 45^{\circ}$. $\because BC = 2$，$\therefore BG = CG=\sqrt{2}$，$\therefore C$点的横坐标为$\sqrt{2}$. 又$C$在反比例函数$y=\frac{4}{x}$的图象上，$\therefore C(\sqrt{2},2\sqrt{2})$.

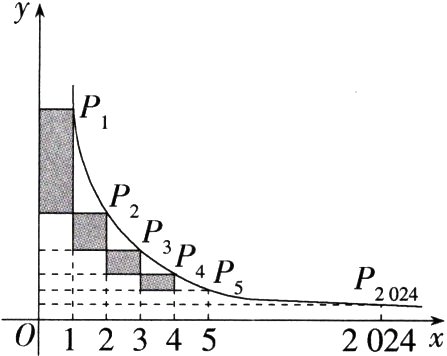
14.(2023山东枣庄中考)如图,在反比例函数$y = \frac{8}{x}(x ＞ 0)$的图象上有$P_1$,$P_2$,$P_3$,…,$P_{2024}$等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作$x$轴与$y$轴的垂线,图中所构成的阴影部分的面积从左到右依次为$S_1$,$S_2$,$S_3$,…,$S_{2023}$,则$S_1 + S_2 + S_3 + \cdots + S_{2023}=$_______.
　　　　　

答案： 答案 $\frac{2023}{253}$
解析 $\because P_1,P_2,P_3,\cdots,P_{2024}$的横坐标依次为 1，2，3，$\cdots$，2024，$\therefore$阴影矩形的一边长都为 1，如图，将除第一个阴影矩形外的所有阴影矩形向左平移至$y$轴，可得$S_1 + S_2+S_3+\cdots+S_{2023}=S_{矩形ABP_1D}$，把$x = 2024$代入$y=\frac{8}{x}$，得$y=\frac{1}{253}$，即$OA=\frac{1}{253}$，$\therefore S_{矩形OABC}=OA\cdot OC=\frac{1}{253}$，由$k$的几何意义得$S_{矩形OCP_1D}=8$，$\therefore S_{矩形ABP_1D}=8-\frac{1}{253}=\frac{2023}{253}$，即$S_1 + S_2+S_3+\cdots+S_{2023}=\frac{2023}{253}$.

15.(8分)(2024江苏苏州姑苏期中)已知反比例函数$y = \frac{k}{x}(k\neq 0)$的图象经过$A(-4,-2)$.
(M9226002)
(1)求反比例函数表达式.
(2)若点$B(m,m - 2)$在该函数图象上,求$m$的值.

答案： 解析
(1)$\because$反比例函数$y=\frac{k}{x}(k\neq0)$的图象经过$A(-4,-2)$，
$\therefore$将$A(-4,-2)$代入$y=\frac{k}{x}$，得$k = -4\times(-2)=8$，
$\therefore$反比例函数的表达式为$y=\frac{8}{x}$.
(2)$\because$点$B(m,m - 2)$在这个函数图象上，
$\therefore$把$B(m,m - 2)$代入$y=\frac{8}{x}$，得$m - 2=\frac{8}{m}$，
解得$m = 4$或$m = -2$，$\therefore m$的值为 4 或 -2.

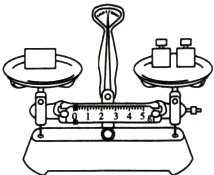
16.(10分)(2024江西景德镇三模)如图,在物理实验课上,小明通过动手操作发现,在左边托盘(固定)中放置一个重物,在右边托盘(可左右移动)中放置一定质量的砝码,可使得天平左右平衡.右边托盘中的砝码质量$m$随着右边托盘与天平中间立柱的距离$d$变化而变化,已知$m$与$d$是反比例函数关系,下面是它们的部分对应值:(M9226004)
　　
(1)根据表格数据求出$m$关于$d$的函数解析式.
(2)当砝码质量为12克时,求右边托盘与天平中间立柱的距离$d$.
　　　　　　　　　　　　　

答案： 解析
(1)设$m$关于$d$的函数解析式为$m=\frac{k}{d}$，
当$d = 5$时，$m = 30$，$\therefore \frac{k}{5}=30$，解得$k = 150$，
$\therefore m$关于$d$的函数解析式为$m=\frac{150}{d}$.
(2)把$m = 12$代入$m=\frac{150}{d}$，得$\frac{150}{d}=12$，解得$d = 12.5$.
答：当砝码质量为 12 克时，右边托盘与天平中间立柱的距离$d$为 12.5 厘米.