《2025年5年中考3年模拟九年级数学下册人教版》

6.(教材变式·P75例4)(2022广西河池中考)如图，小敏在数学实践活动中，利用所学知识对她所在小区居民楼AB的高度进行测量，从小敏家阳台C测得点A的仰角为33°，测得点B的俯角为45°，已知观测点到地面的高度CD = 36 m，求居民楼AB的高度(结果保留整数.参考数据：sin 33°≈0.54，cos 33°≈0.84，tan 33°≈0.65).
(M9228005)

答案：
解析 如图，过点C作CE⊥AB于E，
由题知CD = 36 m，∠BCE = 45°，∠ACE = 33°.
在Rt△BCE中，∠BCE = 45°，
∴BE = CE = CD = 36 m.
在Rt△ACE中，∠ACE = 33°，CE = 36 m，
∴AE = CE·tan 33°≈23.4(m)，
∴AB = AE + BE = 23.4 + 36 = 59.4≈59(m).
答：居民楼AB的高度约为59 m.

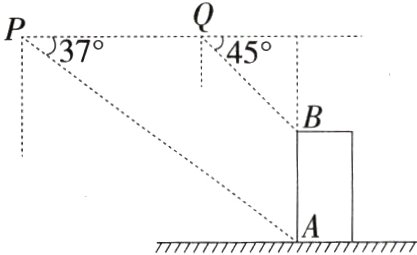
7.(2024江苏盐城中考,15,★★☆)如图，小明用无人机测量教学楼的高度，将无人机垂直上升至距地面30 m的点P处，测得教学楼底端点A的俯角为37°，再将无人机沿教学楼方向水平飞行26.6 m至点Q处，测得教学楼顶端点B的俯角为45°，则教学楼AB的高度约为________m.
(答案精确到1 m，参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75)(M9228005)

答案：
答案 17
解析 如图，设AB的延长线与PQ的延长线交于点C，由题意知，AC = 30 m，PQ = 26.6 m，∠APC = 37°，∠BQC = 45°，在Rt△APC中，PC = $\frac{AC}{\tan 37^{\circ}}\approx\frac{30}{0.75}=40$(m)，
∴QC = PC - PQ = 40 - 26.6 = 13.4(m)，在Rt△BQC中，∠BQC = 45°，
∴BC = QC = 13.4 m，
∴AB = AC - BC = 30 - 13.4 = 16.6≈17(m).

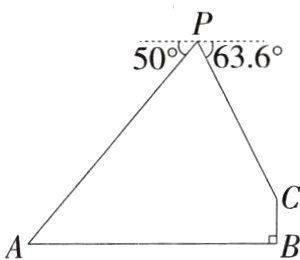
8.(2024山东泰安中考,15,★★☆)在综合实践课上，数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一只无人机如图，无人机在河上方距水面高60米的点P处测得瞭望台正对岸A处的俯角为50°，测得瞭望台顶端C处的俯角为63.6°，已知瞭望台BC高12米(图中点A，B，C，P在同一平面内)，那么大汶河此河段的宽AB为________米.$\left(参考数据：\sin 40^{\circ}\approx\frac{3}{5},\sin 63.6^{\circ}\approx\frac{9}{10},\tan 50^{\circ}\approx\frac{6}{5},\tan 63.6^{\circ}\approx2\right)$

答案： 答案 74
解析 如图，过P作PE⊥AB于E，过C作CF⊥PE于F，由题意知∠NPC = ∠PCF = 63.6°，∠MPA = ∠BAP = 50°，BC = EF = 12 m，PE = 60 m，
∴PF = PE - EF = 48 m，在Rt△PFC中，tan 63.6° = $\frac{PF}{CF}\approx2$，
∴CF≈24 m，
∴BE = CF = 24 m，在Rt△APE中，tan 50° = $\frac{PE}{AE}\approx\frac{6}{5}$，
∴AE≈50 m，
∴AB = AE + BE = 74 m.

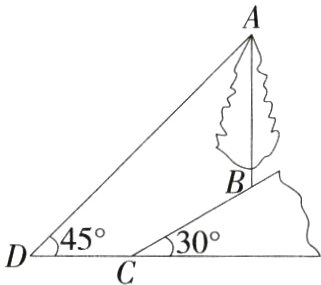
9.(2024内蒙古通辽中考,20,★★☆)在“综合与实践”活动课上，活动小组测量一棵杨树的高度.如图，从C点测得杨树底端B点的仰角是30°，BC长6米，在距离C点4米处的D点测得杨树顶端A点的仰角为45°，求杨树AB的高度(精确到0.1米，AB，BC，CD在同一平面内，点C，D在同一水平线上，参考数据：$\sqrt{3}$≈1.73).

答案：
解析 如图，延长AB交直线DC于H，则∠AHD = 90°，
∵∠BCH = 30°，BC = 6米，
∴BH = $\frac{1}{2}BC = 3$米，CH = $\frac{\sqrt{3}}{2}BC = 3\sqrt{3}$米，
∵∠ADC = 45°，
∴AH = DH = CD + CH = ($4 + 3\sqrt{3}$)米，
∴AB = AH - BH = $4 + 3\sqrt{3}-3 = 1 + 3\sqrt{3}\approx6.2$(米).
答：杨树AB的高度约为6.2米.