《2025年5年中考3年模拟九年级数学下册人教版》

1.(2024天津滨海新区二模)sin 30° - $\frac{1}{2}$的值等于(M9228002)( )
A.-1
B.0
C.1
D.$\sqrt{2}$

答案： 1B 原式=$\frac{1}{2}-\frac{1}{2}$=0.故选B.

2.(2023山东威海文登一模)利用科学计算器计算$\frac{1}{2}\cos 35^{\circ}$，下列按键顺序正确的是(M9228003)( )
A.1 $a^{b/c}$ 2 $\cos$ 3 5 =
B.2 $a^{b/c}$ 1 $\cos$ 3 5 =
C.1 - 2 $\cos$ 3 5 =
D.$a^{b/c}$ 1 2 $\cos$ 3 5 =

答案： 2A 利用科学计算器计算$\frac{1}{2}\cos35^{\circ}$，按键顺序为1 a/b 2 cos 3 5 =.故选A.

3.(2024重庆北碚期末)如图，在Rt△ABC中，∠ACB = 90°，BC : AB = 12 : 13，则tan A的值是(M9228001)( )

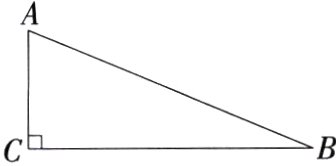
A.$\frac{12}{5}$
B.$\frac{5}{12}$
C.$\frac{12}{13}$
D.$\frac{5}{13}$

答案： 3A
∵$BC:AB = 12:13$，
∴令$BC = 12x$，$AB = 13x$，
∵$\angle ACB = 90^{\circ}$，
∴$AC=\sqrt{AB^{2}-BC^{2}} = 5x$，
∴$\tan A=\frac{BC}{AC}=\frac{12x}{5x}=\frac{12}{5}$.故选A.

4.新独家原创 在△ABC中，∠A，∠B均为锐角，且满足sin B = $\sqrt{\cos A - \frac{1}{2}} - \sqrt{\frac{1}{2} - \cos A} + \frac{\sqrt{2}}{2}$，则∠C的度数为(M9228002)( )
A.60°
B.75°
C.90°
D.105°

答案： 4B 由题意，得$\cos A-\frac{1}{2}\geq0$，$\frac{1}{2}-\cos A\geq0$，
∴$\cos A-\frac{1}{2}=0$，
∴$\cos A=\frac{1}{2}$，$\sin B=\frac{\sqrt{2}}{2}$，
∴$\angle A = 60^{\circ}$，$\angle B = 45^{\circ}$，
∴$\angle C = 180^{\circ}-\angle A-\angle B = 180^{\circ}-60^{\circ}-45^{\circ}=75^{\circ}$.故选B.

5.(2024江苏泗阳致远中学二模)如图，AD是△ABC的高.若BD = 2CD = 6，tan C = 2，则边AB的长为( )

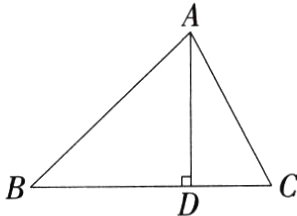
A.3$\sqrt{2}$
B.3$\sqrt{5}$
C.3$\sqrt{7}$
D.6$\sqrt{2}$

答案： 5D
∵$2CD = 6$，
∴$CD = 3$，
∵$\tan C = 2$，
∴$\frac{AD}{CD}=2$，
∴$AD = 6$，在$Rt\triangle ABD$中，由勾股定理得$AB=\sqrt{AD^{2}+BD^{2}}=\sqrt{6^{2}+6^{2}}=6\sqrt{2}$.故选D.

6.(2024广东佛山南海模拟)下表是小亮填写的实践活动报告的部分内容，设树顶到地面的高度DC = x米，根据已知条件列出的求树高的方程正确的为(M9228005)( )

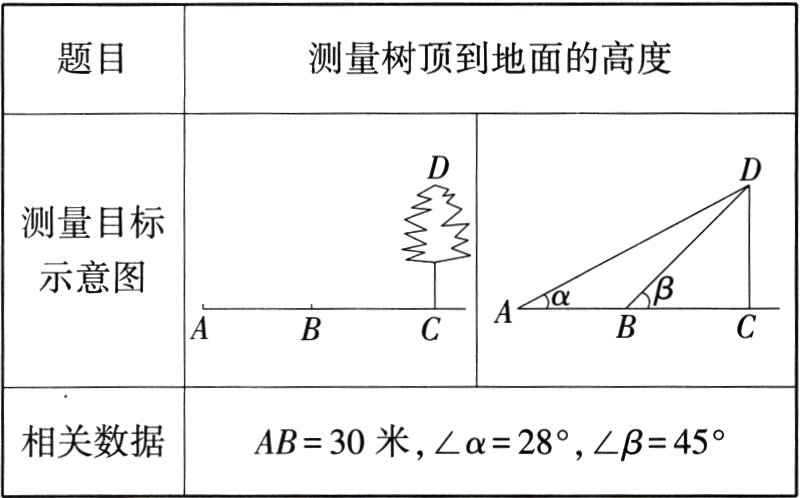
A.x = (x - 30)tan 28°
B.x = (30 + x)tan 28°
C.x + 30 = xtan 28°
D.x - 30 = xtan 28°

答案： 6B 由题意得$DC\perp AC$，在$Rt\triangle DBC$中，$\angle DBC = 45^{\circ}$，$DC = x$米，
∴$BC=\frac{DC}{\tan45^{\circ}}=x$米，
∵$AB = 30$米，
∴$AC = AB + BC=(x + 30)$米，在$Rt\triangle ACD$中，$\angle DAC = 28^{\circ}$，
∴$CD = AC\cdot\tan28^{\circ}=(x + 30)\cdot\tan28^{\circ}$米，
∴$x=(30 + x)\tan28^{\circ}$.故选B.

7.情境题·数学文化(2022江西景德镇模拟)刘徽是我国魏晋时期卓越的数学家，他在《九章算术注》中提出了“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的周长.如图，正十二边形的边长是4，则可求出此十二边形的周长来近似代替其外接圆的周长，便可估计π的值，下面关于π的值表述正确的是( )

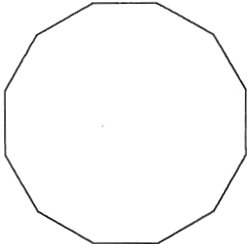
A.π ≈ $\frac{6}{\sin 15^{\circ}}$
B.π ≈ $\frac{12}{\sin 15^{\circ}}$
C.π ≈ 6sin 15°
D.π ≈ 12sin 15°

答案：
7D 如图（$O$为正十二边形的中心），由正十二边形的性质可知，$AM=\frac{1}{2}AB = 2$，$\angle AOB=\frac{360^{\circ}}{12}=30^{\circ}$，则$\angle AOM=\frac{1}{2}\angle AOB = 15^{\circ}$，在$Rt\triangle AOM$中，$OA=\frac{AM}{\sin15^{\circ}}=\frac{2}{\sin15^{\circ}}$，
∵正十二边形的边长为4，
∴正十二边形的周长为$4×12 = 48$，
∴$\pi\approx\frac{48}{2\cdot\frac{2}{\sin15^{\circ}}}=12\sin15^{\circ}$.故选D.