《2025年5年中考3年模拟九年级数学下册人教版》

14. 新考法 推理能力 (2024河南周口太康期末)如图，等边△ABC的边长为20，动点P从点B出发沿BC运动到点C，连接AP，作∠APD = 60°，PD交AC于点D，CD的最大值为__________.
　　　　　　　　

答案： 答案 5
解析 设BP=x(0≤x≤20),CD=y,
∵等边△ABC的边长为20,
∴AB = BC = 20,∠B = ∠C = 60°,
∵∠APC = ∠APD + ∠CPD = ∠B + ∠BAP,∠APD = 60°,
∴∠BAP = ∠CPD,
∴△ABP∽△PCD,
∴$\frac{AB}{PC}=\frac{BP}{CD}$,即$\frac{20}{20 - x}=\frac{x}{y}$,
∴y=$-\frac{1}{20}x²+x=-\frac{1}{20}(x - 10)²+5$,当x = 10时,y有最大值,最大值为5,
∴CD的最大值为5.

15. 分类讨论思想 推理能力 (2023辽宁本溪二模)如图，CD是Rt△ABC斜边AB上的中线，AB = 10，BC = 6，点E、F在边AC上，连接DE，DF，且∠DEF = ∠B，若△DEF与△DBC相似，则线段CF的长为__________.(M9227004)
　　　　　　　

答案： 答案 $\frac{7}{4}$或$\frac{25}{8}$
解析
∵CD是Rt△ABC斜边AB上的中线,AB = 10,
∴CD=$\frac{1}{2}AB = AD = BD = 5$,
∵BC = 6,
∴AC=$\sqrt{AB² - BC²}=8$.△BDC是等腰三角形,∠BDC为顶角,∠B为底角,∠DEF=∠B,所以△DEF与△DBC相似时,△DEF也是等腰三角形,∠DEF为底角,则∠EDF或∠DFE为顶角.当△BDC∽△EDF时,∠DFE = ∠DEF,
∴∠DFC = ∠DEA,
∵CD = DA,
∴∠DCA = ∠A,
∴△DFC≌△DEA(AAS),
∴CF = AE,
∵∠DEF = ∠B,∠A + ∠B = 90°,
∴∠DCA + ∠DEF = 90°,
∴∠CDE = 90°,
∴∠CDE = ∠ACB,
∵∠DCE = ∠A,
∴△DCE∽△CAB,
∴$\frac{CE}{AB}=\frac{CD}{AC}$,
∴$\frac{CE}{10}=\frac{5}{8}$,
∴CE=$\frac{25}{4}$,
∴CF=AE=AC - CE=8-$\frac{25}{4}=\frac{7}{4}$;当△BDC∽△EFD时,∠DFE = ∠BDC,
∵∠DFE = ∠FCD + ∠FDC,∠BDC = ∠FCD + ∠A,
∴∠FDC = ∠A,
∵∠DCF = ∠ACD,
∴△DFC∽△ADC,
∴$\frac{DC}{AC}=\frac{CF}{CD}$,
∴$\frac{5}{8}=\frac{CF}{5}$,
∴CF=$\frac{25}{8}$.综上所述,CF的长为$\frac{7}{4}$或$\frac{25}{8}$.

1.(2024河南南阳十三中月考)已知:如图,△ABC 中,CE⊥AB,BF⊥AC,求证:$\frac{AE}{AF}$=$\frac{AC}{BA}$.

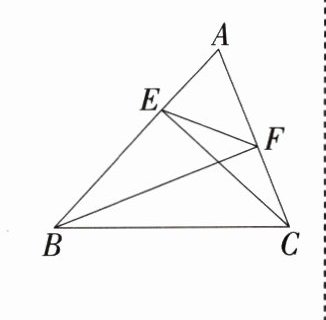
答案： 证明
∵$CE\perp AB$，$BF\perp AC$，
∴$\angle AFB = \angle AEC$；
　
∵$\angle A$为公共角，
∴$\triangle ABF\backsim\triangle ACE$，
　
∴$\frac{AE}{AF}=\frac{AC}{BA}$。

2.(2024湖南衡阳成章实验中学月考)如图,已知△ABC中,AD平分∠BAC,EF是AD的垂直平分线,交BC的延长线于F,连接AF,求证:
$DF^{2}=BF\cdot CF$.

答案： 证明
∵$AD$平分$\angle BAC$，
∴$\angle BAD = \angle CAD$，
　
∵$EF$是$AD$的垂直平分线，
∴$AF = DF$，
　
∴$\angle FAD = \angle ADF$，
　
∵$\angle FAD = \angle FAC+\angle CAD$，$\angle ADF = \angle BAD+\angle B$，
∴$\angle FAC = \angle B$，
　
∵$\angle AFC = \angle AFB$，
　
∴$\triangle FAC\backsim\triangle FBA$，
　
∴$\frac{AF}{BF}=\frac{CF}{AF}$，
∴$AF^{2}=BF\cdot CF$，
　
∵$AF = DF$，
∴$DF^{2}=BF\cdot CF$。

3.如图,梯形ABCD中,AD//BC,AC与BD相交于O点,过点B作BE//CD交CA的延长线于点E.求证:
$OC^{2}=OA\cdot OE$.

答案： 证明
∵$CD// BE$，
∴$\triangle OCD\backsim\triangle OEB$，
　
∴$\frac{OD}{OB}=\frac{OC}{OE}$。
　
∵$AD// BC$，
∴$\triangle ODA\backsim\triangle OBC$，
　
∴$\frac{OD}{OB}=\frac{OA}{OC}$，
　
∴$\frac{OC}{OE}=\frac{OA}{OC}$，即$OC^{2}=OA\cdot OE$。