《2025年学霸高考黑题物理人教版》

经典真题1 缩放圆法(2020·全国Ⅲ卷)真空中有一匀强磁场,磁场边界为两个半径分别为$a$和$3a$的同轴圆柱面,磁场的方向与圆柱轴线平行,其横截面如图所示.一速率为$v$的电子从圆心沿半径方向进入磁场.已知电子质量为$m$,电荷量为$e$,忽略重力.为使该电子的运动被限制在图中实线圆围成的区域内,磁场的磁感应强度最小为
(C)


A.$\frac{3mv}{2ae}$
B.$\frac{mv}{ae}$
C.$\frac{3mv}{4ae}$
D.$\frac{3mv}{5ae}$

答案：
1.【学霸三步解题思路】
步骤A 题干正向延伸
直接信息：
①环形匀强磁场,方向垂直于纸面向里
②磁场内边界是半径为$a$的圆,外边界是半径为$3a$的圆
③电子质量为$m$,电荷量为$e$,速率为$v$,从圆心沿半径方向进入磁场
④电子未射出磁场外边界
间接信息：
电子沿径向射入环形磁场,根据圆(环)形磁场运动轨迹的对称性,电子必沿径向射出磁场
步骤B 设问反向推演
求磁场的磁感应强度最小值
$\Leftrightarrow$对应电子运动的最大运动半径
$\Leftrightarrow$电子运动轨迹与磁场外边界相切时,半径有最大值
$\Leftrightarrow$作出相切情况下的运动轨迹图,找到圆心,连接磁场圆心、切点,构造直角三角形
$\Leftrightarrow$根据勾股定理,建立一元二次方程
步骤C 正反连接
$eBv = m\frac{v^2}{r} \Rightarrow B = \frac{mv}{er}$,$(3a - r_{max})^2 = r_{max}^2 + a^2$
【答案】C
解析:电子在磁场中做匀速圆周运动，由洛伦兹力提供向心力$eBv = m\frac{v^2}{r}$，
则磁感应强度与圆周运动轨迹关系为$B = \frac{mv}{er}$，
即运动轨迹半径越大，磁场的磁感应强度越小。令电子运动轨迹最大的半径为$r_{max}$，为了使电子的运动被限制在图中实线圆围成的区域内，其最大半径的运动轨迹与实线圆相切，如图所示:

A点为电子做圆周运动的圆心，电子从圆心沿半径方向进入磁场，$AB \perp OB$，$\triangle ABO$为直角三角形，则由几何关系可得
$(3a - r_{max})^2 = r_{max}^2 + a^2$，
解得$r_{max} = \frac{4}{3}a$，
解得磁场的磁感应强度最小值$B_{min} = \frac{mv}{er_{max}} = \frac{3mv}{4ae}$
故选C。
名师点评：带电粒子沿径向射入圆形磁场,则必定沿径向射出圆形磁场。环形磁场也有这种对称性。

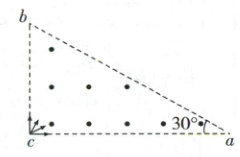
巩固训练2 旋转圆法(2025·湖北武汉二模)如图所示,直角三角形$abc$中$\angle a = 30°$,$ac = L$,其区域内存在磁感应强度大小为$B$、方向垂直纸面向外的匀强磁场,$c$点处的粒子源可向磁场区域各个方向发射速度大小为$\frac{kBL}{2}$($k$为粒子的比荷)的带正电的粒子.不考虑粒子的重力和相互间作用力,下列说法正确的是
(C)


A.$ab$边上有粒子到达区域的长度为$\frac{\sqrt{3}}{3}L$
B.$ac$边上有粒子到达区域的长度为$\frac{1}{2}L$
C.从$ab$边射出的粒子在磁场中运动的最短时间为$\frac{\pi}{3kB}$
D.从$ac$边射出的粒子在磁场中运动的最长时间为$\frac{\pi}{2kB}$

答案：
2. 题型分析
本题考查了带电粒子在有界磁场中的极值问题,以及几何关系求解。带电粒子运动轨迹对应的圆心角越大,时间越长。
C 解析：AB.粒子在磁场中由洛伦兹力提供向心力,得$qvB = m\frac{v^2}{r}$，
解得$r = \frac{mv}{qB} = \frac{L}{2}$，如图甲、乙所示:
　　　
由几何关系可得$ab$边上有粒子到达区域的长度为$\Delta L_{ab} = ad - ae = 2 × \frac{L}{2} \cos 30^{\circ} - (L \cos 30^{\circ} - \frac{L}{2}) = \frac{L}{2}$，由几何关系可得$ac$边上有粒子到达区域的长度为$\Delta L_{ac} = 2r \cos 30^{\circ} = \frac{\sqrt{3}}{2}L$，故AB错误；C.如图丙所示:

粒子从$ab$边上$d$点射出时,对应的圆心角最小,所用时间最短,由几何关系可知,最小圆心角为$60^{\circ}$，则最短时间为$t_{min} = \frac{60^{\circ}}{360^{\circ}}T = \frac{1}{6} × \frac{2 \pi m}{qB} = \frac{\pi m}{3qB}$，故C正确；D.如图丁所示:

粒子从$ac$边上$f$点射出时,对应的圆心角最大,所用时间最长,由几何关系可知,最大圆心角为$120^{\circ}$，则最长时间为$t_{max} = \frac{120^{\circ}}{360^{\circ}}T = \frac{1}{3} × \frac{2 \pi m}{qB} = \frac{2 \pi m}{3qB}$，故D错误。故选C。
名师点评：根据洛伦兹力充当向心力求出运动半径,再结合几何关系求解。这里面要清晰运动轨迹和$ab$直线相切时,运动到最远点,对应的圆心角最大,运动时间最长。

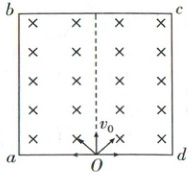
巩固训练3 旋转圆法(2025·广东佛山二模)如图所示,边长为$L$的正方形$abcd$区域内有匀强磁场,$ad$边中点处$O$有一粒子源,向磁场内各方向均匀发射速率均为$v_0$的电子,$ab$边恰好没有电子射出,已知电子质量为$m$,电量大小为$e$,则
(D)

A.$bc$边有电子射出

B.磁感应强度大小为$\frac{mv_0}{eL}$
C.从$ad$边射出的电子在磁场中运动的最长时间为$\frac{\pi L}{12v_0}$
D.从$cd$边射出的电子数和从$ad$边射出的电子数比值为$5:1$

答案：
3. 题型分析
本题属于矩形磁场中的运动问题,电子速度大小固定,方向不定,适用旋转圆法,找到临界位置。
D 解析：AB.$ab$边恰好没有电子射出,轨迹如图所示(轨迹1)，

根据洛伦兹力提供向心力有$ev_0B = m\frac{v_0^2}{r}$，所以$B = \frac{2mv_0}{eL}$，由于电子射入的速度大小不变,方向改变,则轨迹半径不变,根据旋转圆模型可知,$bc$边没有电子射出,故AB错误；C.从$ad$边射出的电子在磁场中运动的时间最长时轨迹如图所示,

根据几何关系可知,圆心角$\theta = 60^{\circ}$，所以最长时间为$t = \frac{\theta}{360^{\circ}}T = \frac{60^{\circ}}{360^{\circ}} × \frac{2 \pi r}{v_0} = \frac{\pi L}{6v_0}$，故C错误；D.由以上分析可知,当粒子恰好经过$d$点时,其入射速度方向与$ad$边的夹角为$30^{\circ}$，所以从$cd$边射出的电子数和从$ad$边射出的电子数比值为$\frac{150^{\circ}}{30^{\circ}} = \frac{5}{1}$，故D正确。故选D。
解题技巧：依据条件,确定临界情况下的电子的轨迹,根据几何关系求得运动的轨迹半径,根据洛伦兹力提供向心力求得磁感应强度,根据运动的轨迹的圆心角越大,运动的时间越长进行分析。依据电子出射时的速度方向与$ad$边夹角的范围,求解从$cd$边射出的电子数和$ad$边射出的电子数比值。

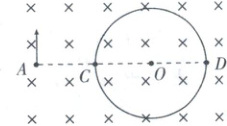
巩固训练4 缩放圆法(2023·T8联考)如图,磁感应强度大小为$B$的匀强磁场垂直于纸面向里.点$A$、$C$、$O$、$D$处于一条水平线上,且$AC = CO = OD = r$.$A$处有一个粒子源,竖直向上同时射出速率不同的同种带电粒子,粒子经过以$O$为圆心、$r$为半径的圆周上各点.已知粒子质量为$m$,电量的绝对值为$q$,不计粒子重力和粒子间相互作用力,问:
(1)粒子带正电荷还是负电荷?到达$C$和到达$D$处的粒子的速率比$v_1:v_2$;
(2)求粒子到达圆周所需的最短时间$T_{\min}$及最先到达圆周的粒子的速度大小$v_3$.

答案：
4. 题型分析
本题属于缩放圆模型,结合圆形接收屏的问题。考查运动时间最短时的轨迹判断及作图求解。
(1)负电荷$v_1 : v_2 = 1 : 3$
(2)$T_{min} = \frac{2 \pi m}{3qB}$ $v_3 = \frac{qBr}{m}$
解析：
(1)由左手定则得,粒子带负电。
由洛伦兹力提供向心力得
$\frac{qv_1B}{r_1} = m\frac{v_1^2}{r_1}$，$\frac{qv_2B}{r_2} = m\frac{v_2^2}{r_2}$，
由几何关系得
$r_1 = \frac{r}{2}$，$r_2 = \frac{3r}{2}$，
联立解得$v_1 : v_2 = 1 : 3$。
(2)根据$qvB = m\frac{v^2}{r}$，$T = \frac{2 \pi r}{v}$，
解得$T = \frac{2 \pi m}{qB}$
可见周期与速度无关。所以粒子运动的轨迹对应的圆心角越小,时间越短。由几何关系得,当轨迹圆弧所对应的弦与圆相切时,时间最短。如图：

此时$\cos \theta = \frac{r}{2r} = \frac{1}{2}$，
解得$\theta = \frac{\pi}{3}$，
则$T_{min} = \frac{2 \theta}{2 \pi}T = \frac{2 \pi m}{3qB}$，
时间最短,则该粒子最先到达。
由$\frac{qv_3B}{r} = m\frac{v_3^2}{r}$，解得$v_3 = \frac{qBr}{m}$
解题技巧：判断轨迹圆心角何时最小时,不用考虑轨迹形状,只看入射点和出射点(轨迹与圆弧的交点)连线,该连线与$AO$之间的夹角越大,则轨迹的圆心角越小。这样很容易判断出当连线与圆相切时,轨迹的圆心角最小,运动时间最短。