《2025年学霸高考黑题物理人教版》

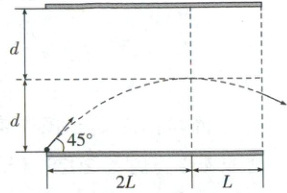
经典真题1(偏转电场+类斜抛运动)(2023·湖北卷)(多选)一带正电微粒从静止开始经电压$U_1$加速后，射入水平放置的平行板电容器，极板间电压为$U_2$。微粒射入时紧靠下极板边缘，速度方向与极板夹角为$45^{\circ}$，微粒运动轨迹的最高点到极板左右两端的水平距离分别为$2L$和$L$，到两极板距离均为$d$，如图所示。忽略边缘效应，不计重力。下列说法正确的是(BD)


A.$L:d = 2:1$
B.$U_1:U_2 = 1:1$
C.微粒穿过电容器区域的偏转角度的正切值为$2$
D.仅改变微粒的质量或者电荷数量，微粒在电容器中的运动轨迹不变

答案： 1.【学霸三步解题思路】
步骤A 题干正向延伸
直接信息：
①加速电压$U_1$，板间电压$U_2$
②板间距离$2d$，极板长度$3L$
③斜抛运动初速度方向与水平方向成$45°$角，竖直方向最大位移为$d$
间接信息：
①射入到最高点的时间：最高点到射出的时间$=2:1$
②水平分速度=竖直分速度
步骤B 设问反向推演
选项A：$L、d$的比值$\Rightarrow$从入射到最高点的斜抛运动的竖直位移与水平位移
选项B：$U_1、U_2$的比值$\Rightarrow U_1$决定入射初速度，$U_2$决定竖直位移
选项C：速度偏转角的正切值$\Rightarrow$通过从最高点到射出的平抛运动计算竖直速度
选项D：影响粒子运动轨迹的因素$\Rightarrow$射入到最高点的平抛运动(逆向思维)与最高点到射出的平抛运动的轨迹方程
步骤C 正反连接
选项A：$v_{x}t_{1}=2L,\frac {0+v_{y}}{2}t_{1}=d$
选项B：$a = \frac{qE}{m}=\frac{qU_{2}}{2md}$，$v_{y}^{2}=2ad$，$qU_{1}=\frac{1}{2}mv_{0}^{2}$
选项C：$v_{x}t_{2}=L$，$v_{y1}=at_{2}$，$v_{y}=at_{1}$，$t_{2}=\frac{1}{2}t_{1}$，$\tan\alpha=\frac{v_{y1}}{v_{x}}$，偏转角=$\alpha + 45^{\circ}$
选项D：$qU_{1}=\frac{1}{2}mv_{0}^{2}$，从射入到最高点：$x_{1}=v_{x}t_{1}$，$y_{1}=v_{y}t_{1}-\frac{1}{2}· \frac{qU_{2}}{2md}· t_{1}^{2}$；从最高点到射出：$x_{2}=v_{x}t_{2}$，$y_{2}=\frac{1}{2}· \frac{qU_{2}}{2md}· t_{2}^{2}$
【答案】BD
解析：B.微粒在电容器中水平方向做匀速直线运动，竖直方向做匀变速直线运动，根据电场强度和电势差的关系及场强和电场力的关系可得$E = \frac{U_{2}}{2d}$，$F = qE = ma$，微粒射入电容器后的速度为$v_{0}$，水平方向和竖直方向的分速度$v_{x}=v_{0}\cos45^{\circ}=\frac{\sqrt{2}}{2}v_{0}$，$v_{y}=v_{0}\sin45^{\circ}=\frac{\sqrt{2}}{2}v_{0}$，从射入到运动到最高点由运动学关系$v_{y}^{2}=2ad$，微粒射入电场时由动能定理可得$qU_{1}=\frac{1}{2}mv_{0}^{2}$，联立解得$U_{1}:U_{2}=1:1$，B正确；
解题技巧：$U_{1}$决定了微粒入射的初动能，$qU_{1}=\frac{1}{2}mv_{0}^{2}$，微粒在极板间消耗微粒竖直方向速度对应的动能，$q· \frac{1}{2}U_{2}=\frac{1}{2}mv_{y}^{2}$，由于$v_{0}:v_{y}=\sqrt{2}:1$，则$U_{1}:\frac{1}{2}U_{2}=v_{0}^{2}:v_{y}^{2}=2:1$，即$U_{1}:U_{2}=1:1$。
A.微粒从射入到运动到最高点由运动学可得$2L = v_{x}t_{1}$，$d=\frac{0 + v_{y}}{2}t_{1}$，联立可得$L:d = 1:1$，A错误；C.微粒穿出电容器时从最高点到穿出时由运动学可得$v_{x}t_{2}=L$，$v_{y1}=at_{2}$，射入电容器到最高点有$v_{y}=at_{1}$，由于$t_{2}=\frac{1}{2}t_{1}$，得$v_{y1}=\frac{v_{y}}{2}$，设微粒穿出电容器时速度与水平的夹角为$\alpha$，则$\tan\alpha=\frac{v_{y1}}{v_{x}}=\frac{1}{2}$，微粒射入电容器时速度和水平方向的夹角为$\beta = 45^{\circ}$，$\tan(\alpha + \beta)=\frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta}=3$，C错误；D.微粒射入到最高点的过程中水平方向的位移为$x_{1}=v_{x}t_{1}$，竖直方向的位移为$y_{1}=v_{y}t_{1}-\frac{1}{2}· \frac{qU_{2}}{2md}· t_{1}^{2}$，联立$qU_{1}=\frac{1}{2}mv_{0}^{2}$，$v_{x}=v_{y}=v_{0}\cos45^{\circ}$，解得$y_{1}=x_{1}-\frac{U_{2}x_{1}^{2}}{4dU_{1}}$，最高点到射出电容器过程，同理可得$x_{2}=L = v_{x}t_{2}$，$y_{2}=\frac{1}{2}· \frac{qU_{2}}{2md}· t_{2}^{2}$，解得$y_{2}=\frac{U_{2}x_{2}^{2}}{4dU_{1}}$，即轨迹不会变化，D正确。故选BD。