2025年学霸高考黑题物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学霸高考黑题物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
巩固训练 3 弹性碰撞 + 圆周运动 + 运动分解 (2025·湖北十一校二模)在竖直平面内,质量 $m = 0.1\ kg$ 的小球 $A$ 用长为 $L = 0.5\ m$ 的不可伸长的轻绳悬挂于 $O$ 点,$O$ 点正下方用 $L = 0.5\ m$ 不可伸长的轻绳竖直悬挂一质量也为 $0.1\ kg$ 的小球 $B$。把小球 $A$ 拉到如图所示位置,轻绳恰好伸直,且轻绳与竖直方向的夹角 $\alpha = 60°$。由静止释放小球 $A$,$A$ 球自由下落,两小球发生弹性碰撞。两球都可视为质点,忽略空气阻力,$g$ 取 $10\ m/s^2$。下列说法正确的是(
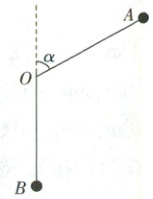
A.小球 $A$ 在与小球 $B$ 发生碰撞前小球 $A$ 的速度大小为 $\sqrt{15}\ m/s$
B.小球 $A$ 在与小球 $B$ 发生碰撞后小球 $B$ 的速度大小为 $\dfrac{5\sqrt{2}}{2}\ m/s$
C.小球 $A$ 和小球 $B$ 发生碰撞后,小球 $B$ 上升的最大高度与小球 $A$ 释放的高度相同
D.小球 $A$ 和小球 $B$ 发生碰撞后小球 $B$ 在上摆的过程中轻绳不会松弛
B
)
A.小球 $A$ 在与小球 $B$ 发生碰撞前小球 $A$ 的速度大小为 $\sqrt{15}\ m/s$
B.小球 $A$ 在与小球 $B$ 发生碰撞后小球 $B$ 的速度大小为 $\dfrac{5\sqrt{2}}{2}\ m/s$
C.小球 $A$ 和小球 $B$ 发生碰撞后,小球 $B$ 上升的最大高度与小球 $A$ 释放的高度相同
D.小球 $A$ 和小球 $B$ 发生碰撞后小球 $B$ 在上摆的过程中轻绳不会松弛
答案:
3.题型分析
速度分解、弹性碰撞—动碰静模型、竖直方向圆周运动的临界问题.
B 解析:A.小球A先做自由落体运动至关于过O点的水平线对称的位置,由机械能守恒定律得$mgL=\frac{1}{2}mv_0^2$,
得$v_0=\sqrt{10} m/s$,在此位置绳绷直的瞬间,把$v_0$沿绳和垂直绳方向分解,沿绳方向分速度由于绳拉力的冲量而变为0,仅剩下垂直绳方向分速度沿弧线下摆至B处,机械能守恒,$v_{⊥}=v_0\sin 60^{\circ}=\frac{\sqrt{30}}{2} m/s$,设A与B碰前速度为$v_1$,由机械能守恒定律得
$mgL(1-\cos 60^{\circ})=\frac{1}{2}mv_1^2-\frac{1}{2}mv_{⊥}^2$,解得$v_1=\frac{5\sqrt{2}}{2} m/s$,故A错误;
易错提醒:注意原题中的条件“不可伸长的轻绳”,这意味着在绳子绷直的瞬间,小球在沿着绳子方向上的分速度会瞬间归零,此时小球沿着绳子方向上的动能瞬间转化为内能
B.A和B发生弹性碰撞,根据动量守恒$mv_1=mv_1'+mv_B$,根据机械能守恒$\frac{1}{2}mv_1^2=\frac{1}{2}mv_1'^2+\frac{1}{2}mv_B^2$,解得$v_1'=0$,$v_B=\frac{5\sqrt{2}}{2} m/s$,故B正确;
C.由于小球A下落至绳绷直时有机械能损失,故B球上升的最大高度一定小于A球释放高度,故C错误;D.由于B球不能做完整的圆周运动,要想绳子不松弛,小球不能过圆心等高位置(本题图中O点).设B上升的最大高度为h,对小球B上摆过程由机械能守恒定律得$mgh=\frac{1}{2}mv_B^2$,解得$h=\frac{5}{8} m>0.5 m$,越过了圆心高度,绳会松弛,故D错误.故选B.

3.题型分析
速度分解、弹性碰撞—动碰静模型、竖直方向圆周运动的临界问题.
B 解析:A.小球A先做自由落体运动至关于过O点的水平线对称的位置,由机械能守恒定律得$mgL=\frac{1}{2}mv_0^2$,
得$v_0=\sqrt{10} m/s$,在此位置绳绷直的瞬间,把$v_0$沿绳和垂直绳方向分解,沿绳方向分速度由于绳拉力的冲量而变为0,仅剩下垂直绳方向分速度沿弧线下摆至B处,机械能守恒,$v_{⊥}=v_0\sin 60^{\circ}=\frac{\sqrt{30}}{2} m/s$,设A与B碰前速度为$v_1$,由机械能守恒定律得
$mgL(1-\cos 60^{\circ})=\frac{1}{2}mv_1^2-\frac{1}{2}mv_{⊥}^2$,解得$v_1=\frac{5\sqrt{2}}{2} m/s$,故A错误;
易错提醒:注意原题中的条件“不可伸长的轻绳”,这意味着在绳子绷直的瞬间,小球在沿着绳子方向上的分速度会瞬间归零,此时小球沿着绳子方向上的动能瞬间转化为内能
B.A和B发生弹性碰撞,根据动量守恒$mv_1=mv_1'+mv_B$,根据机械能守恒$\frac{1}{2}mv_1^2=\frac{1}{2}mv_1'^2+\frac{1}{2}mv_B^2$,解得$v_1'=0$,$v_B=\frac{5\sqrt{2}}{2} m/s$,故B正确;
C.由于小球A下落至绳绷直时有机械能损失,故B球上升的最大高度一定小于A球释放高度,故C错误;D.由于B球不能做完整的圆周运动,要想绳子不松弛,小球不能过圆心等高位置(本题图中O点).设B上升的最大高度为h,对小球B上摆过程由机械能守恒定律得$mgh=\frac{1}{2}mv_B^2$,解得$h=\frac{5}{8} m>0.5 m$,越过了圆心高度,绳会松弛,故D错误.故选B.

巩固训练 4 弹性碰撞 + 子母球问题 + 极限思维 (2025·湖南长郡二十校联盟联考)三个同质且均匀分布的弹性小球 $A、B、C$ 通过质心的光滑细杆相互接触串在一起,如图,三球质量满足 $m_A\gg m_B\gg m_C$。现将三小球竖直从离地面高为 $h$ 处静止自由下落,若所有碰撞均可视为弹性碰撞,则小球 $C$ 上跳的高度约为(
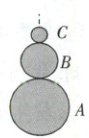
A.$25h$
B.$49h$
C.$16h$
D.$3h$
B
)
A.$25h$
B.$49h$
C.$16h$
D.$3h$
答案:
4.题型分析
一般弹性碰撞模型、自由落体与竖直上抛运动.
B 解析:根据动能定理$mgh=\frac{1}{2}mv_0^2$,解得三球在落地前均有向下的速度为$v_0=\sqrt{2gh}$,A球先与地面弹性碰撞后速度变为向上的$v_0$与B球发生碰撞,取向上为正方向,根据动量守恒和机械能守恒有$m_Av_0-m_Bv_0=m_Av_{A1}+m_Bv_{B1}$,$\frac{1}{2}m_Av_0^2+\frac{1}{2}m_Bv_0^2=\frac{1}{2}m_Av_{A1}^2+\frac{1}{2}m_Bv_{B1}^2$,解得A、B发生弹性碰撞后B的速度大小为$v_{B1}=\frac{(3m_A-m_B)v_0}{m_A+m_B}$,因为$m_A\gg m_B$,则有$v_{B1}=3v_0$,此后B、C发生弹性碰撞,取向上为正方向,根据动量守恒和机械能守恒有$m_B· 3v_0-m_Cv_0=m_Bv_{B2}+m_Cv_C$,$\frac{1}{2}m_B(3v_0)^2+\frac{1}{2}m_Cv_0^2=\frac{1}{2}m_Bv_{B2}^2+\frac{1}{2}m_Cv_C^2$,解得$v_C=\frac{(7m_B-m_C)v_0}{m_B+m_C}$,因为$m_B\gg m_C$,则有$v_C=7v_0$,根据动能定理$\frac{1}{2}m_Cv_C^2=m_Cgh_C$,其中$v_0=\sqrt{2gh}$,解得$h_C=49h$,故选B.
解题技巧:本题利用弹性碰撞速算式,即$v_A-v_B=v_B'-v_A'$,可以快速求解.A撞地反弹后与B碰撞前相对速度大小为$2v_0$,由于$m_A\gg m_C$,A与B碰撞后速度不变,根据结论,B的速度应该为$3v_0$,这样才能保证弹性碰撞前后相对速度大小一样.同理可以判断出B与C碰撞后,B速度不变,C的速度应该为$v_0+3v_0+3v_0=7v_0$.最终$h_C=49h$.
一般弹性碰撞模型、自由落体与竖直上抛运动.
B 解析:根据动能定理$mgh=\frac{1}{2}mv_0^2$,解得三球在落地前均有向下的速度为$v_0=\sqrt{2gh}$,A球先与地面弹性碰撞后速度变为向上的$v_0$与B球发生碰撞,取向上为正方向,根据动量守恒和机械能守恒有$m_Av_0-m_Bv_0=m_Av_{A1}+m_Bv_{B1}$,$\frac{1}{2}m_Av_0^2+\frac{1}{2}m_Bv_0^2=\frac{1}{2}m_Av_{A1}^2+\frac{1}{2}m_Bv_{B1}^2$,解得A、B发生弹性碰撞后B的速度大小为$v_{B1}=\frac{(3m_A-m_B)v_0}{m_A+m_B}$,因为$m_A\gg m_B$,则有$v_{B1}=3v_0$,此后B、C发生弹性碰撞,取向上为正方向,根据动量守恒和机械能守恒有$m_B· 3v_0-m_Cv_0=m_Bv_{B2}+m_Cv_C$,$\frac{1}{2}m_B(3v_0)^2+\frac{1}{2}m_Cv_0^2=\frac{1}{2}m_Bv_{B2}^2+\frac{1}{2}m_Cv_C^2$,解得$v_C=\frac{(7m_B-m_C)v_0}{m_B+m_C}$,因为$m_B\gg m_C$,则有$v_C=7v_0$,根据动能定理$\frac{1}{2}m_Cv_C^2=m_Cgh_C$,其中$v_0=\sqrt{2gh}$,解得$h_C=49h$,故选B.
解题技巧:本题利用弹性碰撞速算式,即$v_A-v_B=v_B'-v_A'$,可以快速求解.A撞地反弹后与B碰撞前相对速度大小为$2v_0$,由于$m_A\gg m_C$,A与B碰撞后速度不变,根据结论,B的速度应该为$3v_0$,这样才能保证弹性碰撞前后相对速度大小一样.同理可以判断出B与C碰撞后,B速度不变,C的速度应该为$v_0+3v_0+3v_0=7v_0$.最终$h_C=49h$.
巩固训练 5 一般对心碰撞 + $v - t$ 图像 (2025·广东卷)如图所示,光滑水平面上,小球 $M、N$ 分别在水平恒力 $F_1$ 和 $F_2$ 作用下,由静止开始沿同一直线相向运动,在 $t_1$ 时刻发生正碰后各自反向运动。已知 $F_1$ 和 $F_2$ 始终大小相等,方向相反。从开始运动到碰撞后第 $1$ 次速度减为 $0$ 的过程中,两小球速度 $v$ 随时间 $t$ 变化的图像,可能正确的是(
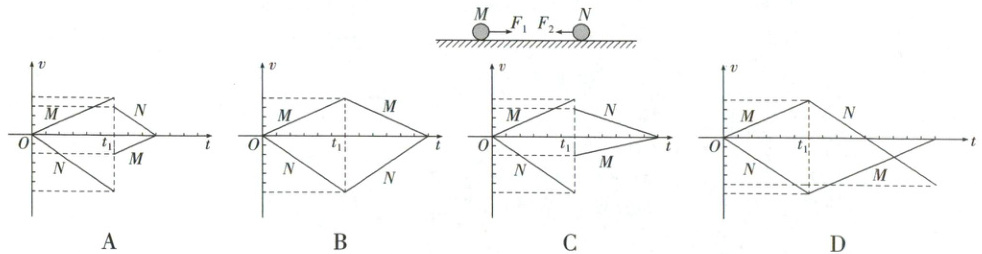
A
)
答案:
5.题型分析
一般对心碰撞、$v-t$图像.
A 解析:根据牛顿第二定律$a=\frac{F}{m}$,两物体受外力F大小相等,由图像的斜率等于加速度可知M、N的加速度大小之比为$4:6=2:3$,可知M、N的质量之比为$6:4=3:2$;设分别为$3m$和$2m$;由图像可设M、N碰前的速度分别为$4v$和$6v$,则因M、N系统受合外力为零,向右为正方向,则系统动量守恒,则由动量守恒定律$3m· 4v-2m· 6v=3mv_1+2mv_2$,
若系统为弹性碰撞,则由机械能守恒可知$\frac{1}{2}· 3m(4v)^2+\frac{1}{2}· 2m(6v)^2=\frac{1}{2}· 3mv_1^2+\frac{1}{2}· 2mv_2^2$,
解得$v_1=-4v$,$v_2=6v$.
因M、N的加速度大小之比仍为$2:3$,则停止运动的时间之比为$1:1$,即两物体一起停止;
若不是弹性碰撞,则$3m· 4v-2m· 6v=3mv_1+2mv_2$,
可知碰后速度大小之比为$v_1:v_2=2:3$,
若假设$v_1=2v$,则$v_2=3v$,此时满足$\frac{1}{2}· 3m(4v)^2+\frac{1}{2}· 2m(6v)^2>\frac{1}{2}· 3mv^2+\frac{1}{2}· 2mv^2$,
则假设成立,因M、N的加速度大小之比仍为$2:3$,则停止运动的时间之比为$1:1$,对M来说碰撞前后的速度之比为$4v:2v=2:1$,可知碰撞前后运动时间之比为$2:1$,可知A正确,BCD错误.故选A.
解析技巧:B.碰后瞬间M、N速度大小方向不变,两球穿越违反常识,排除.D.根据图像,两球碰后速度交换,根据两等质量球弹性正碰速度交换的规律,反推两球质量相等,图像斜率大小不同,排除.C.因为力恒定,碰撞前后球M或N的加速度不变,图中M或N前后不平行,排除.只能选A.
一般对心碰撞、$v-t$图像.
A 解析:根据牛顿第二定律$a=\frac{F}{m}$,两物体受外力F大小相等,由图像的斜率等于加速度可知M、N的加速度大小之比为$4:6=2:3$,可知M、N的质量之比为$6:4=3:2$;设分别为$3m$和$2m$;由图像可设M、N碰前的速度分别为$4v$和$6v$,则因M、N系统受合外力为零,向右为正方向,则系统动量守恒,则由动量守恒定律$3m· 4v-2m· 6v=3mv_1+2mv_2$,
若系统为弹性碰撞,则由机械能守恒可知$\frac{1}{2}· 3m(4v)^2+\frac{1}{2}· 2m(6v)^2=\frac{1}{2}· 3mv_1^2+\frac{1}{2}· 2mv_2^2$,
解得$v_1=-4v$,$v_2=6v$.
因M、N的加速度大小之比仍为$2:3$,则停止运动的时间之比为$1:1$,即两物体一起停止;
若不是弹性碰撞,则$3m· 4v-2m· 6v=3mv_1+2mv_2$,
可知碰后速度大小之比为$v_1:v_2=2:3$,
若假设$v_1=2v$,则$v_2=3v$,此时满足$\frac{1}{2}· 3m(4v)^2+\frac{1}{2}· 2m(6v)^2>\frac{1}{2}· 3mv^2+\frac{1}{2}· 2mv^2$,
则假设成立,因M、N的加速度大小之比仍为$2:3$,则停止运动的时间之比为$1:1$,对M来说碰撞前后的速度之比为$4v:2v=2:1$,可知碰撞前后运动时间之比为$2:1$,可知A正确,BCD错误.故选A.
解析技巧:B.碰后瞬间M、N速度大小方向不变,两球穿越违反常识,排除.D.根据图像,两球碰后速度交换,根据两等质量球弹性正碰速度交换的规律,反推两球质量相等,图像斜率大小不同,排除.C.因为力恒定,碰撞前后球M或N的加速度不变,图中M或N前后不平行,排除.只能选A.
巩固训练 6 弹性碰撞 + 圆周运动 + 动能定理 (2025·广东佛山二模)很多医院都装备有气动物流装置,将药房配药输送到各科室。如图所示是类似的气动输送装置,管道 $abcde$ 右端开口,其中 $ab$ 竖直,高度 $H = 2R$,$bc$ 是半径为 $R$ 的四分之一圆弧管($R$ 远大于管道直径),$cde$ 水平,$cd$ 长度 $x_1 = 3R$,$de$ 长度 $x_2 = \dfrac{10}{3}R$。$d$ 处紧挨放置着大小可忽略不计的运输胶囊 $B$ 和 $C$,$B$ 被锁定在 $d$ 处,$a$ 处放置胶囊 $A$,胶囊与管道内壁接触处均不漏气,胶囊 $A、C$ 间气室为真空,$A$ 的质量为 $m$,$B、C$ 的质量均为 $M = 3m$。启动风机,给 $A$ 施加一大小恒为 $F = 2mg$ 的气动推力,$A$ 运动至 $d$ 处前瞬间解锁 $B$,并与 $B$ 完成弹性碰撞,紧接着 $B$ 与 $C$ 完成弹性碰撞,碰撞时间极短,大气对 $C$ 产生的压力恒为 $mg$(忽略管道内空气流动对气压的影响),$ab$ 和 $cde$ 均光滑,$A$ 经 $bc$ 过程克服阻力做功为 $W_f = mgR(\pi - 1)$,求:
(1)$A$ 经圆弧管 $b$ 点处时,管道对其弹力大小 $F_N$;
(2)$B$ 与 $C$ 碰撞后瞬间,$C$ 的速度大小 $v_C$;
(3)试分析并判断 $B$ 与 $C$ 是否会发生第二次碰撞。
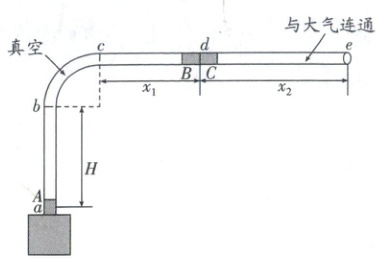
(1)$A$ 经圆弧管 $b$ 点处时,管道对其弹力大小 $F_N$;
(2)$B$ 与 $C$ 碰撞后瞬间,$C$ 的速度大小 $v_C$;
(3)试分析并判断 $B$ 与 $C$ 是否会发生第二次碰撞。

答案:
6.题型分析
弹性碰撞模型、动能定理、二次碰撞的判断问题.
(1)$4mg$
(2)$2\sqrt{gR}$
(3)B与C不会发生二次碰撞
解析:
(1)A由a到b过程$(F-mg)×2R=\frac{1}{2}mv_b^2$,解得$v_b=2\sqrt{gR}$,
A经b点处$F_N=m\frac{v_b^2}{R}$,解得$F_N=4mg$.
(2)A由b到d过程$F×\frac{\pi R}{2}-W_1-mgR+F_x=\frac{1}{2}mv_d^2-\frac{1}{2}mv_b^2$,解得$v_d=4\sqrt{gR}$,
A与B碰撞,以$v_d$的方向为正方向,有$mv_d=mv_A+Mv_B$,$\frac{1}{2}mv_d^2+\frac{1}{2}Mv_B^2=\frac{1}{2}mv_A^2+\frac{1}{2}Mv_B^2$,
解得$v_A=-2\sqrt{gR}$,$v_B=2\sqrt{gR}$,
B与C碰撞,以$v_B$的方向为正方向,有$Mv_B=Mv_{B2}+Mv_C$,$\frac{1}{2}Mv_B^2=\frac{1}{2}Mv_{B2}^2+\frac{1}{2}Mv_C^2$,
解得$v_{B2}=0$,$v_C=2\sqrt{gR}$.
(3)设管de段足够长,B与C会发生二次碰撞,先设A反弹不会进入圆弧管,则A减速至速度为零所需距离为$s_1$,则$-Fs_1=0-\frac{1}{2}mv_A^2$,解得$s_1=R<x_1=3R$,假设成立,
以$v_A$的方向为正方向,则A与B两次碰撞时间间隔为$t_1$,则$Ft_1=m(-v_A)-mv_A$,解得$t_1=2\sqrt{\frac{R}{g}}$
A与B从第一次碰撞到第二次碰撞C的位移为$x_C=v_Ct_1-\frac{1}{2}at_1^2$,
C的加速度大小$mg=Ma$,解得$a=\frac{1}{3}g$,
位移大小为$x_C=\frac{10}{3}R$,此时C恰好到达管口处,即B与C不会发生二次碰撞.
弹性碰撞模型、动能定理、二次碰撞的判断问题.
(1)$4mg$
(2)$2\sqrt{gR}$
(3)B与C不会发生二次碰撞
解析:
(1)A由a到b过程$(F-mg)×2R=\frac{1}{2}mv_b^2$,解得$v_b=2\sqrt{gR}$,
A经b点处$F_N=m\frac{v_b^2}{R}$,解得$F_N=4mg$.
(2)A由b到d过程$F×\frac{\pi R}{2}-W_1-mgR+F_x=\frac{1}{2}mv_d^2-\frac{1}{2}mv_b^2$,解得$v_d=4\sqrt{gR}$,
A与B碰撞,以$v_d$的方向为正方向,有$mv_d=mv_A+Mv_B$,$\frac{1}{2}mv_d^2+\frac{1}{2}Mv_B^2=\frac{1}{2}mv_A^2+\frac{1}{2}Mv_B^2$,
解得$v_A=-2\sqrt{gR}$,$v_B=2\sqrt{gR}$,
B与C碰撞,以$v_B$的方向为正方向,有$Mv_B=Mv_{B2}+Mv_C$,$\frac{1}{2}Mv_B^2=\frac{1}{2}Mv_{B2}^2+\frac{1}{2}Mv_C^2$,
解得$v_{B2}=0$,$v_C=2\sqrt{gR}$.
(3)设管de段足够长,B与C会发生二次碰撞,先设A反弹不会进入圆弧管,则A减速至速度为零所需距离为$s_1$,则$-Fs_1=0-\frac{1}{2}mv_A^2$,解得$s_1=R<x_1=3R$,假设成立,
以$v_A$的方向为正方向,则A与B两次碰撞时间间隔为$t_1$,则$Ft_1=m(-v_A)-mv_A$,解得$t_1=2\sqrt{\frac{R}{g}}$
A与B从第一次碰撞到第二次碰撞C的位移为$x_C=v_Ct_1-\frac{1}{2}at_1^2$,
C的加速度大小$mg=Ma$,解得$a=\frac{1}{3}g$,
位移大小为$x_C=\frac{10}{3}R$,此时C恰好到达管口处,即B与C不会发生二次碰撞.
查看更多完整答案,请扫码查看


