《2025年学霸高考黑题物理人教版》

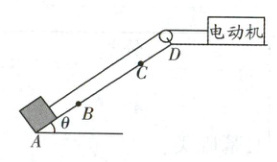
经典真题1 斜面模型+能量守恒+牛顿第二定律 (2024·江苏卷)如图所示,粗糙斜面的动摩擦因数为$\mu$,倾角为$\theta$,斜面长为$L$.一个质量为$m$的物块,在电动机作用下,从$A$点由静止加速至$B$点时达到最大速度$v$,之后做匀速运动至$C$点,关闭电动机,从$C$点又恰好到达最高点$D$.已知重力加速度大小为$g$,求：
(1)$CD$段长$x$;
(2)$BC$段电动机的输出功率$P$;
(3)全过程物块增加的机械能$E_{1}$和电动机消耗的总电能$E_{2}$的比值.

答案： 1.【学霸三步解题思路】
步骤A 题干正向延伸
直接信息：
①斜面的动摩擦因数为$\mu$，倾角为$\theta$，斜面长为$L$
②从$A$点由静止加速至$B$点时达到最大速度$v$
③$BC$阶段以$v$的速度匀速运动
④关闭电动机，从$C$点又恰好到达最高点$D$
间接信息：
①$BC$匀速阶段物块受力平衡，电动机的牵引力$F = mg\sin \theta + \mu mg\cos \theta$
②$CD$阶段做匀减速运动，初速度为$v$，末速度$0$，满足$mg\sin \theta + \mu mg\cos \theta = ma$，
则$a = g\sin \theta + \mu g\cos \theta$
③全过程中物块受到的摩擦力$f = \mu mg\cos \theta$
步骤B 设问反向推演
(1)求$CD$段长$x$
$\Rightarrow$根据间接信息已知初速度$v$、末速度$0$、加速度$a$
$\Rightarrow$根据匀变速直线运动的速度位移关系求解
(2)求$BC$段电动机的输出功率$P$
$\Rightarrow P = Fv$
(3)求全过程物块增加的机械能$E_1$和电动机消耗的总电能$E_2$的比值
$\Rightarrow$全过程初末速度都为$0$，故动能不变，则增加的机械能为增加的重力势能
$\Rightarrow$增加的高度$h = L\sin \theta$
$\Rightarrow E_1 = mgh$
$\Rightarrow$根据能量守恒，电动机消耗的总电能为物块增加的机械能加上此过程中摩擦产生的热量
$\Rightarrow Q = fL, E_2 = E_1 + Q$
步骤C 正反连接
(1)$mg\sin \theta + \mu mg\cos \theta = ma, 0 - v^2 = -2ax$
解得$x = \frac{v^2}{2g(\sin \theta + \mu \cos \theta)}$
(2)$F = mg\sin \theta + \mu mg\cos \theta, P = Fv$
解得$P = mgv(\sin \theta + \mu \cos \theta)$
(3)$E_1 = mgL\sin \theta, E_2 = E_1 + \mu mg\cos \theta · L$
解得$\frac{E_1}{E_2} = \frac{mgL\sin \theta}{mgL\sin \theta + \mu mgL\cos \theta} = \frac{\sin \theta}{\sin \theta + \mu \cos \theta}$
【答案】
(1)$\frac{v^2}{2g(\sin \theta + \mu \cos \theta)}$
(2)$mgv(\sin \theta + \mu \cos \theta)$
(3)$\frac{\sin \theta}{\sin \theta + \mu \cos \theta}$
解析：
(1)物块在$CD$段运动过程中，由牛顿第二定律得$mg\sin \theta + \mu mg\cos \theta = ma$，
由运动学公式得$0 - v^2 = -2ax$，
联立解得$x = \frac{v^2}{2g(\sin \theta + \mu \cos \theta)}$。
(2)物块在$BC$段匀速运动，得电动机的牵引力为$F = mg\sin \theta + \mu mg\cos \theta$，
由$P = Fv$得$P = mgv(\sin \theta + \mu \cos \theta)$。
(3)全过程物块增加的机械能为$E_1 = mgL\sin \theta$，
整个过程能量守恒得电动机消耗的总电能转化为物块增加的机械能和摩擦产生的内能，故可知
$E_2 = E_1 + \mu mg\cos \theta · L$，
故可得$\frac{E_1}{E_2} = \frac{mgL\sin \theta}{mgL\sin \theta + \mu mgL\cos \theta} = \frac{\sin \theta}{\sin \theta + \mu \cos \theta}$

经典真题2 斜面弹簧模型+牛顿第二定律+动能定理 (2021·福建卷)如图(a),一倾角为$37^{\circ}$的固定斜面的$AB$段粗糙,$BC$段光滑.斜面上一轻质弹簧的一端固定在底端$C$处,弹簧的原长与$BC$长度相同.一小滑块在沿斜面向下的拉力$T$作用下,由$A$处从静止开始下滑,当滑块第一次到达$B$点时撤去$T.T$随滑块沿斜面下滑的位移$s$的变化关系如图(b)所示.已知$AB$段长度为$2\ m$,滑块质量为$2\ kg$,滑块与斜面$AB$段的动摩擦因数为$0.5$.弹簧始终在弹性限度内,重力加速度大小取$10\ m/s^2$,$\sin37^{\circ}=0.6$.求：
(1)当拉力为$10\ N$时,滑块的加速度大小;
(2)滑块第一次到达$B$点时的动能;
(3)滑块第一次在$B$点与弹簧脱离后,沿斜面上滑的最大距离.

答案： 2.【学霸三步解题思路】
步骤A 题干正向延伸
直接信息：
①固定斜面倾角为$37°$，$AB$段粗糙，$BC$段光滑，$AB$段长度为$2m$
②弹簧的原长与$BC$长度相同
③滑块质量为$2kg$，滑块与斜面$AB$段的动摩擦因数为$0.5$
间接信息：
滑块第一次在$B$点与弹簧脱离的动能与第一次在$B$点接触弹簧的动能相同
步骤B 设问反向推演
(1)求拉力为$10N$时，滑块的加速度
$\Rightarrow$对滑块受力分析并正交分解
$\Rightarrow$利用牛顿第二定律求得加速度
(2)求滑块第一次到达$B$点时的动能
$\Rightarrow$根据图像求拉力$T$做的功
$\Rightarrow$根据动能定理求得动能
(3)求滑块第一次在$B$点与弹簧脱离后，沿斜面上滑的最大距离
$\Rightarrow$对滑块脱离弹簧到沿斜面上滑减速到$0$的过程使用动能定理，求得最大距离
步骤C 正反连接
(1)$T + mg\sin \theta - f = ma, N - mg\cos \theta = 0, f = \mu N$
(2)$W = T_1s_1 + T_2s_2, W + (mg\sin \theta - f)(s_1 + s_2) = E_k - 0$
(3)$- (mg\sin \theta + f)s_{max} = 0 - E_k$
【答案】
(1)$7m/s^2$
(2)$26J$
(3)$1.3m$
解析：
(1)设小滑块的质量为$m$，斜面倾角为$\theta$，滑块与斜面间的动摩擦因数为$\mu$，滑块受斜面的支持力大小为$N$，滑动摩擦力大小为$f$，拉力为$10N$时滑块的加速度大小为$a$。由牛顿第二定律和滑动摩擦力公式有
$T + mg\sin \theta - f = ma·s·s①$，
$N - mg\cos \theta = 0·s·s②$，
$f = \mu N·s·s③$，
联立①②③式并代入题给数据得$a = 7m/s^2·s·s④$。
(2)设滑块在$AB$段运动的过程中拉力所做的功为$W$，由功的定义有
$W = T_1s_1 + T_2s_2·s·s⑤$，
式中$T_1$、$T_2$和$s_1$、$s_2$分别对应滑块下滑过程中两阶段所受的拉力及相应的位移大小。
依题意，$T_1 = 8N$，$s_1 = 1m$，$T_2 = 10N$，$s_2 = 1m$。
设滑块第一次到达$B$点时的动能为$E_k$，由动能定理有$W + (mg\sin \theta - f)(s_1 + s_2) = E_k - 0·s·s⑥$，
联立②③⑤⑥式并代入题给数据得$E_k = 26J·s·s⑦$。
(3)由机械能守恒定律可知，滑块第二次到达$B$点时，动能仍为$E_k$。设滑块离$B$点的最大距离为$s_{max}$，由动能定理有$- (mg\sin \theta + f)s_{max} = 0 - E_k·s·s⑧$，
联立②③⑦⑧式并代入题给数据得$s_{max} = 1.3m$。