《2025年学霸高考黑题物理人教版》

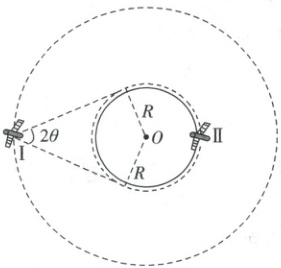
(2025·山东济南三模)如图所示，Ⅰ为北斗卫星导航系统中的静止轨道卫星，其对地张角为2θ，Ⅱ为地球的近地卫星。已知地球的自转周期为$T_{0}$，引力常量为G，根据题中条件，可求出(A)


A.地球的平均密度为$\frac{3\pi}{GT_{0}^{2}\sin^{3}\theta}$
B.卫星Ⅰ和卫星Ⅱ的加速度之比为$1:\sin^{2}2\theta$
C.卫星Ⅱ的周期为$\frac{T_{0}}{\sqrt{\sin^{3}\theta}}$
D.卫星Ⅱ运动的一个周期内无法直接接收到卫星Ⅰ发出电磁波信号的时间为$\frac{(\pi + 2\theta)T_{0}}{2\pi}\sqrt{\sin^{3}\theta}$

答案： 5.题型分析
开普勒第三定律，卫星追及相遇问题.
A 解析：C.设地球质量为$M$，卫星Ⅰ、Ⅱ的轨道半径分别为$r$和$R$，卫星Ⅰ为同步卫星，周期为$T_{0}$，近地卫星Ⅱ的周期为$T$.
根据开普勒第三定律得$\frac{r^{3}}{T_{0}^{2}} = \frac{R^{3}}{T^{2}}$，由题图得$\sin\theta = \frac{R}{r}$，
可得卫星Ⅱ的周期为$T = T_{0}\sqrt{\sin^{3}\theta}$，故C错误；
A.对于卫星Ⅱ有$\frac{GMm}{R^{2}} = m( \frac{2\pi}{T} )^{2}R$，对于地球$\rho = \frac{M}{V} = \frac{3M}{4\pi R^{3}}$，
联立以上各式，可得地球的平均密度为$\rho = \frac{3\pi}{GT_{0}^{2}\sin^{3}\theta}$，故A正确；
B.对于不同轨道卫星，根据牛顿第二定律得$a = \frac{GM}{r^{2}}$，
所以卫星Ⅰ和卫星Ⅱ的加速度之比为$\frac{a_{Ⅰ}}{a_{Ⅱ}} = \frac{R^{2}}{r^{2}} = \sin^{2}\theta$，故B错误；
D.当卫星Ⅱ运行到与卫星Ⅰ的连线隔着地球的区域内，其对应圆心角为$\pi + 2\theta$时，卫星Ⅱ无法直接接收到卫星Ⅰ发出电磁波信号，设这段时间为$t$.若两卫星同向运行，则有
$(\omega_{Ⅱ} - \omega_{Ⅰ})t = \pi + 2\theta$，其中$\omega_{Ⅱ} = \frac{2\pi}{T} = \frac{2\pi}{T_{0}\sqrt{\sin^{3}\theta}}$，$\omega_{Ⅰ} = \frac{2\pi}{T_{0}}$，解得
$t = \frac{2\pi(1 - \sqrt{\sin^{3}\theta})}{2\pi(1 + \sqrt{\sin^{3}\theta})}$
重难突破：卫星追及相遇问题的难点在于同学们对角速度概念的理解不够透彻.角速度$\omega$与线速度$v$本质上是差不多的，角速度是每秒通过的角度，线速度是每秒通过的路程.举个例子，甲、乙两同学沿环形跑道赛跑，经过$t$时间甲比乙多跑一圈，设跑道周长为$L$用线速度列式，$(v_{甲} - v_{乙})t = L$；用角速度列式，$(\omega_{甲} - \omega_{乙})t = 2\pi$.
若两卫星相向运行，则有$\omega_{Ⅱ} = \frac{2\pi}{T} = \frac{2\pi}{T_{0}\sqrt{\sin^{3}\theta}}$，$(\omega_{Ⅱ} + \omega_{Ⅰ})t = \pi + 2\theta$，
$\omega_{Ⅰ} = \frac{2\pi}{T_{0}}$，解得$t = \frac{(\pi + 2\theta)T_{0}\sqrt{\sin^{3}\theta}}{2\pi(1 + \sqrt{\sin^{3}\theta})}$，故D错误.故选A.

压轴挑战6 斜抛运动+天体问题
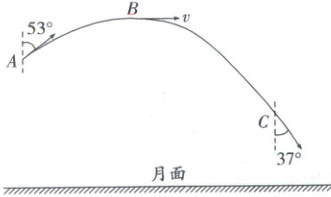
(2025·山东威海月考)中国宇航员计划在2030年前登上月球，假设宇宙飞船落到月面前绕月球表面做角速度为ω的匀速圆周运动，运动半径可近似看为月球半径。宇航员登上月球后，做了一次斜上抛运动的实验。如图所示，在月面上，小球从A点斜向上抛出，经过最高点B运动到C点，已知小球在A、C两点的速度与竖直方向的夹角分别为53°、37°，小球在B点的速度为v，小球从A到C的运动时间为t，引力常量为G，$\sin53° = 0.8$，$\cos53° = 0.6$，忽略月球的自转影响，求：
(1)月球的密度（假设月球为均匀球体）以及月面的重力加速度；
(2)宇宙飞船绕月球表面做匀速圆周运动的线速度大小以及月球的质量。

答案： 6.题型分析
斜抛运动与天体问题结合，黄金代换.
(1)$\frac{3\omega^{2}}{4\pi G}$
(2)$\frac{25v}{12\omega t}$ $\frac{25v}{12\omega t} = \frac{15625v^{3}}{1728Gt\omega^{4}}$
解析：
(1)根据$G\frac{Mm}{R^{2}} = m\omega^{2}R,\rho = \frac{M}{4}\frac{4}{3}\pi R^{3}$，可得$\rho = \frac{3\omega^{2}}{4\pi G}$，
在A点时的竖直速度$v_{Ay} = v\tan37^{\circ} = \frac{3}{4}v$，
在C点时的竖直速度$v_{Cy} = v\tan53^{\circ} = \frac{4}{3}v$，
向上为正，则从A到C由运动公式$-v_{Cy} = v_{Ay} - gt$，
解得$g = \frac{25v}{12t}$.
(2)根据$G\frac{Mm}{R^{2}} = mg = m\omega^{2}R$，可得$R = \frac{g}{\omega^{2}}$.
名师点评：对于地球、月球、火星以及自转速度较慢的未知天体，可以近似地认为其表面物体受到的万有引力等于其重力，这就是“黄金代换”，简化表达式为$GM = gR^{2}$.通常我们在做天体运动相关的选择题时，如果发现选项中没有$GM$却有$g$，那么此题大概率会用到黄金代换.
宇宙飞船绕月球表面做匀速圆周运动的线速度$v_{0} = \omega R = \frac{g}{\omega} = \frac{25v}{12\omega t}$
月球的质量$M = \rho\frac{4}{3}\pi R^{3} = \frac{15625v^{3}}{1728Gt\omega^{4}}$.