2025年学霸高考黑题物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学霸高考黑题物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
巩固训练2(光滑斜面+轻绳模型+$T - \alpha$图像)
(2025·四川遂宁二模)如图甲所示,倾角为$\theta$的光滑斜面固定在水平地面上,细线一端与可看成质点的质量为$m$的小球相连,另一端穿入小孔$O$与力传感器(位于斜面体内部)连接,传感器可实时记录细线拉力大小及扫过的角度。初始时,细线水平,小球位于小孔$O$的右侧,现敲击小球,使小球获得一平行于斜面向上的初速度$v_{0}$,此后传感器记录细线拉力$T$的大小随细线扫过角度$\alpha$的变化图像如图乙所示,图中$F_{0}$已知,小球到$O$点距离为$l$,重力加速度为$g$,则下列说法不正确的是(
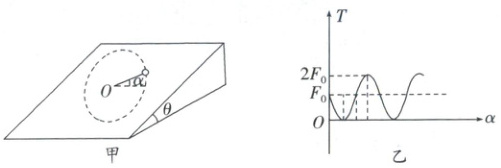
A.小球位于初始位置时的加速度为$\frac{v_{0}^{2}}{l}$
B.小球通过最高点时速度为$\sqrt{gl\sin\theta}$
C.小球通过最高点时速度为$\sqrt{\frac{mgsin\theta}{F_{0}}}v_{0}$
D.小球通过最低点时速度为$\sqrt{\frac{2F_{0} - mgsin\theta}{F_{0}}}v_{0}$
(2025·四川遂宁二模)如图甲所示,倾角为$\theta$的光滑斜面固定在水平地面上,细线一端与可看成质点的质量为$m$的小球相连,另一端穿入小孔$O$与力传感器(位于斜面体内部)连接,传感器可实时记录细线拉力大小及扫过的角度。初始时,细线水平,小球位于小孔$O$的右侧,现敲击小球,使小球获得一平行于斜面向上的初速度$v_{0}$,此后传感器记录细线拉力$T$的大小随细线扫过角度$\alpha$的变化图像如图乙所示,图中$F_{0}$已知,小球到$O$点距离为$l$,重力加速度为$g$,则下列说法不正确的是(
A
)
A.小球位于初始位置时的加速度为$\frac{v_{0}^{2}}{l}$
B.小球通过最高点时速度为$\sqrt{gl\sin\theta}$
C.小球通过最高点时速度为$\sqrt{\frac{mgsin\theta}{F_{0}}}v_{0}$
D.小球通过最低点时速度为$\sqrt{\frac{2F_{0} - mgsin\theta}{F_{0}}}v_{0}$
答案:
2.题型分析
本题属于斜面上的轻绳模型.
A 解析:A.位于初始位置时的向心加速度大小为$a_1=\frac{v_{0}^{2}}{l}$,沿斜面向下的加速度大小为$a_2 = g\sin\theta$,根据平行四边形定则知,小球位于初始位置时的加速度大于$\frac{v_{0}^{2}}{l}$,故A错误,满足题意要求;
B.由图乙可知,小球通过最高点时细线的拉力最小,为零,则有$mg\sin\theta = m\frac{v_{1}^{2}}{l}$,解得小球通过最高点时的速度$v_1 = \sqrt{gl\sin\theta}$,故B正确,不满足题意要求;
C.小球在初始位置时,有$F_0 = m\frac{v_{0}^{2}}{l}$,则小球通过最高点时的速度$v_1 = \sqrt{gl\sin\theta}=\sqrt{\frac{mg\sin\theta}{F_0}}v_0$,故C正确,不满足题意要求;
D.小球通过最低点时,细线的拉力最大,根据牛顿第二定律有$2F_0 - mg\sin\theta = m\frac{v_{2}^{2}}{l}$,联立解得小球通过最低点的速度为$v_2 = \sqrt{\frac{2F_0 - mg\sin\theta}{F_0}}v_0$,故D正确,不满足题意要求.故选A.
本题属于斜面上的轻绳模型.
A 解析:A.位于初始位置时的向心加速度大小为$a_1=\frac{v_{0}^{2}}{l}$,沿斜面向下的加速度大小为$a_2 = g\sin\theta$,根据平行四边形定则知,小球位于初始位置时的加速度大于$\frac{v_{0}^{2}}{l}$,故A错误,满足题意要求;
B.由图乙可知,小球通过最高点时细线的拉力最小,为零,则有$mg\sin\theta = m\frac{v_{1}^{2}}{l}$,解得小球通过最高点时的速度$v_1 = \sqrt{gl\sin\theta}$,故B正确,不满足题意要求;
C.小球在初始位置时,有$F_0 = m\frac{v_{0}^{2}}{l}$,则小球通过最高点时的速度$v_1 = \sqrt{gl\sin\theta}=\sqrt{\frac{mg\sin\theta}{F_0}}v_0$,故C正确,不满足题意要求;
D.小球通过最低点时,细线的拉力最大,根据牛顿第二定律有$2F_0 - mg\sin\theta = m\frac{v_{2}^{2}}{l}$,联立解得小球通过最低点的速度为$v_2 = \sqrt{\frac{2F_0 - mg\sin\theta}{F_0}}v_0$,故D正确,不满足题意要求.故选A.
(2025·云南昭通模拟)如图甲所示为一种“自动旋转电玩小球”玩具模型的简化图。内侧半径为$R$的光滑绝缘轨道竖直固定放置,轨道内部存在与轨道平面平行的匀强电场(方向未知)。轨道内侧有一质量为$m$,带电量为$q(q > 0)$的五彩小球从轨道最低点$P$以某一初速度启动,在轨道平面内沿逆时针方向恰好能做完整的圆周运动。运动过程中,小球与轨道圆心$O$的连线与$OP$方向的夹角记为$\theta$,乙图所示为小球在运动过程中的电势能$E_{p}$随角度$\theta$的变化情况,已知重力加速度为$g$,则(
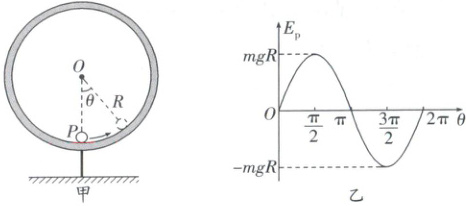
A.匀强电场的方向水平向右
B.电场强度的大小为$\frac{\sqrt{2}mg}{q}$
C.小球运动过程中动能的最小值为$\frac{\sqrt{2}}{2}mgR$
D.小球运动过程中对轨道压力的最大值为$(3 + 3\sqrt{2})mg$
C
)
A.匀强电场的方向水平向右
B.电场强度的大小为$\frac{\sqrt{2}mg}{q}$
C.小球运动过程中动能的最小值为$\frac{\sqrt{2}}{2}mgR$
D.小球运动过程中对轨道压力的最大值为$(3 + 3\sqrt{2})mg$
答案:
3.题型分析
本题属于轻绳模型的变式——轨道模型,结合复合场问题.
C 解析:A.如图所示,

设M、N分别为圆环上与圆心O等高的两点,根据乙图,当$\theta = 0$和$\theta = \pi$时,小球的电势能均为0,则P、Q两点的连线为等势线,当$\theta = \frac{\pi}{2}$时,小球运动到N点,电势能$E_{pN}=mgR$;当$\theta = \frac{3\pi}{2}$时,小球运动到M点,电势能$E_{pM}=-mgR$,综上所得,电场线的方向由N指向M,即水平向左,A错误;
B.小球从N点运动到M点,由动能定理得$Eq·2R = mgR - (-mgR)$,解得$E = \frac{mg}{q}$,B错误;
C.小球所受电场力$F = Eq = mg$,则小球所受合力,即小球在圆环内受到的等效重力为$\sqrt{2}mg$,方向与MN成$45^{\circ}$角,根据题意,小球运动到等效“最高点”时动能最小,由牛顿第二定律得$\sqrt{2}mg = m\frac{v_{min}^{2}}{R}$,解得$\frac{1}{2}mv_{min}^{2}=\frac{\sqrt{2}}{2}mgR$,即$E_{kmin}=\frac{\sqrt{2}}{2}mgR$,C正确;
D.当小球运动到“最低点”时对轨道的压力最大,小球从等效“最高点”到等效“最低点”的过程,根据动能定理得$\sqrt{2}mg·2R = \frac{1}{2}mv_{max}^{2}-\frac{1}{2}mv_{min}^{2}$,小球在等效“最低点”时,根据牛顿第二定律得$F_N - \sqrt{2}mg = m\frac{v_{max}^{2}}{R}$,联立以上两式,解得$F_N = 6\sqrt{2}mg$,D错误.故选C.
3.题型分析
本题属于轻绳模型的变式——轨道模型,结合复合场问题.
C 解析:A.如图所示,

设M、N分别为圆环上与圆心O等高的两点,根据乙图,当$\theta = 0$和$\theta = \pi$时,小球的电势能均为0,则P、Q两点的连线为等势线,当$\theta = \frac{\pi}{2}$时,小球运动到N点,电势能$E_{pN}=mgR$;当$\theta = \frac{3\pi}{2}$时,小球运动到M点,电势能$E_{pM}=-mgR$,综上所得,电场线的方向由N指向M,即水平向左,A错误;
B.小球从N点运动到M点,由动能定理得$Eq·2R = mgR - (-mgR)$,解得$E = \frac{mg}{q}$,B错误;
C.小球所受电场力$F = Eq = mg$,则小球所受合力,即小球在圆环内受到的等效重力为$\sqrt{2}mg$,方向与MN成$45^{\circ}$角,根据题意,小球运动到等效“最高点”时动能最小,由牛顿第二定律得$\sqrt{2}mg = m\frac{v_{min}^{2}}{R}$,解得$\frac{1}{2}mv_{min}^{2}=\frac{\sqrt{2}}{2}mgR$,即$E_{kmin}=\frac{\sqrt{2}}{2}mgR$,C正确;
D.当小球运动到“最低点”时对轨道的压力最大,小球从等效“最高点”到等效“最低点”的过程,根据动能定理得$\sqrt{2}mg·2R = \frac{1}{2}mv_{max}^{2}-\frac{1}{2}mv_{min}^{2}$,小球在等效“最低点”时,根据牛顿第二定律得$F_N - \sqrt{2}mg = m\frac{v_{max}^{2}}{R}$,联立以上两式,解得$F_N = 6\sqrt{2}mg$,D错误.故选C.
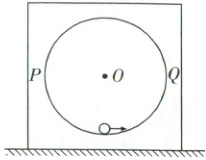
(2025·安徽合肥二模)如图所示,质量为$M$、半径为$R$、内壁光滑的圆形轨道竖直放置在水平地面上,轨道圆心为$O$,$P$、$Q$是轨道上与圆心$O$等高的两点。一质量为$m$的小球沿轨道做圆周运动且刚好能通过轨道最高点,运动过程中轨道始终在地面保持静止状态。已知重力加速度为$g$,求:
(1)小球经过轨道最低点时的速度大小;
(2)小球经过$P$点时,地面对轨道的摩擦力;
(3)轨道对地面的最小压力的大小。
(1)小球经过轨道最低点时的速度大小;
(2)小球经过$P$点时,地面对轨道的摩擦力;
(3)轨道对地面的最小压力的大小。

答案:
4.题型分析
本题属于轻绳模型的变式——轨道模型.
(1)$\sqrt{5gR}$
(2)$3mg$,方向水平向右
(3)$Mg - \frac{3}{4}mg$
解析:
(1)由题意可知,小球恰好通过轨道最高点时,小球的重力恰好提供向心力,则有$mg = m\frac{v_{1}^{2}}{R}$,解得$v_1 = \sqrt{gR}$;
小球从最高点运动到最低点,设小球在最低点的速度为$v_2$,由动能定理可得$mg·2R = \frac{1}{2}mv_{2}^{2}-\frac{1}{2}mv_{1}^{2}$,解得$v_2 = \sqrt{5gR}$.
(2)小球经过P点时,轨道的支持力提供向心力,设速度为$v_3$,小球由最高点运动到P点过程中,由动能定理得$mgR = \frac{1}{2}mv_{3}^{2}-\frac{1}{2}mv_{1}^{2}$,又$F_{N1} = m\frac{v_{3}^{2}}{R}$,解得$F_{N1}=3mg$,方向水平向右.
由牛顿第三定律得,小球对轨道压力$F_{N1}' = F_{N1}=3mg$,方向水平向左.
由二力平衡得,地面对轨道摩擦力$f = F_{N1}' = 3mg$,方向水平向右.
(3)如图所示,

设小球经过A点时速度大小为v,AO连线与竖直方向夹角为$\theta$,
名师点评:虽然“刚好通过最高点”时,小球对轨道没有压力,但不能草率地认为最高点就是对地面压力最小的位置.
在抵达最高点的前后,小球不能脱离轨道,对轨道必然会有压力,因此对地面压力最小的位置应该在圆周左上或右上的某个位置.
由动能定理有$mgR(1 - \cos\theta)=\frac{1}{2}mv^{2}-\frac{1}{2}mv_{1}^{2}$,又$mg\cos\theta + F_N = m\frac{v^{2}}{R}$,解得$F_N = 3mg - 3mg\cos\theta$,
又有$F_N = F_{N}\cos\theta = 3mg\cos\theta - 3mg\cos^{2}\theta$,
根据牛顿第三定律,轨道对地面压力等于地面对轨道的支持力,结合轨道受力平衡可知$F_{压}=F_{支}-F_N = Mg - 3mg(\cos\theta - \cos^{2}\theta)$,
由数学知识得,当$\cos\theta = \frac{1}{2}$时,$F_{压}$取最小值$F_{压min}=Mg - \frac{3}{4}mg$.
4.题型分析
本题属于轻绳模型的变式——轨道模型.
(1)$\sqrt{5gR}$
(2)$3mg$,方向水平向右
(3)$Mg - \frac{3}{4}mg$
解析:
(1)由题意可知,小球恰好通过轨道最高点时,小球的重力恰好提供向心力,则有$mg = m\frac{v_{1}^{2}}{R}$,解得$v_1 = \sqrt{gR}$;
小球从最高点运动到最低点,设小球在最低点的速度为$v_2$,由动能定理可得$mg·2R = \frac{1}{2}mv_{2}^{2}-\frac{1}{2}mv_{1}^{2}$,解得$v_2 = \sqrt{5gR}$.
(2)小球经过P点时,轨道的支持力提供向心力,设速度为$v_3$,小球由最高点运动到P点过程中,由动能定理得$mgR = \frac{1}{2}mv_{3}^{2}-\frac{1}{2}mv_{1}^{2}$,又$F_{N1} = m\frac{v_{3}^{2}}{R}$,解得$F_{N1}=3mg$,方向水平向右.
由牛顿第三定律得,小球对轨道压力$F_{N1}' = F_{N1}=3mg$,方向水平向左.
由二力平衡得,地面对轨道摩擦力$f = F_{N1}' = 3mg$,方向水平向右.
(3)如图所示,

设小球经过A点时速度大小为v,AO连线与竖直方向夹角为$\theta$,
名师点评:虽然“刚好通过最高点”时,小球对轨道没有压力,但不能草率地认为最高点就是对地面压力最小的位置.
在抵达最高点的前后,小球不能脱离轨道,对轨道必然会有压力,因此对地面压力最小的位置应该在圆周左上或右上的某个位置.
由动能定理有$mgR(1 - \cos\theta)=\frac{1}{2}mv^{2}-\frac{1}{2}mv_{1}^{2}$,又$mg\cos\theta + F_N = m\frac{v^{2}}{R}$,解得$F_N = 3mg - 3mg\cos\theta$,
又有$F_N = F_{N}\cos\theta = 3mg\cos\theta - 3mg\cos^{2}\theta$,
根据牛顿第三定律,轨道对地面压力等于地面对轨道的支持力,结合轨道受力平衡可知$F_{压}=F_{支}-F_N = Mg - 3mg(\cos\theta - \cos^{2}\theta)$,
由数学知识得,当$\cos\theta = \frac{1}{2}$时,$F_{压}$取最小值$F_{压min}=Mg - \frac{3}{4}mg$.
查看更多完整答案,请扫码查看


