《2025年学霸高考黑题物理人教版》

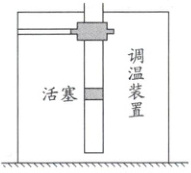
压轴挑战 6 竖直单活塞+热力学第一定律（2025·山东卷）如图所示，上端开口，下端封闭的足够长玻璃管竖直固定于调温装置内。玻璃管导热性能良好，管内横截面积为 $S$，用轻质活塞封闭一定质量的理想气体。大气压强为 $p_0$，活塞与玻璃管之间的滑动摩擦力大小恒为 $f_0 = \frac{1}{21}p_0S$，等于最大静摩擦力。用调温装置对封闭气体缓慢加热，$T_1 = 330\ K$ 时，气柱高度为 $h_1$，活塞开始缓慢上升；继续缓慢加热至 $T_2 = 440\ K$ 时停止加热，活塞不再上升；再缓慢降低气体温度，活塞位置保持不变，直到降温至 $T_3 = 400\ K$ 时，活塞才开始缓慢下降；温度缓慢降至 $T_4 = 330\ K$ 时，保持温度不变，活塞不再下降。求：
(1) $T_2 = 440\ K$ 时，气柱高度 $h_2$；
(2) 从 $T_1$ 状态到 $T_4$ 状态的过程中，封闭气体吸收的净热量 $Q$（扣除放热后净吸收的热量）。

答案： 6.题型分析
本题属于单缸单活塞问题，考查理想气体状态方程与热力学第一律的综合应用.
(1)$\frac{4}{3}h_1$
(2)$\frac{8p_0h_1S}{63}$
解析：
(1)活塞开始缓慢上升，由受力平衡$p_0S + f_0 = p_1S$，
可得封闭的理想气体压强$p_1 = \frac{22}{21}p_0$，
$T_1 \to T_2$升温过程中，等压膨胀，由盖－吕萨克定律$\frac{h_1S}{T_1} = \frac{h_2S}{T_2}$，解得$h_2 = \frac{4}{3}h_1$.
(2)$T_1 \to T_2$升温过程中，等压膨胀，外界对气体做功$W_1 = -p_1(h_2 - h_1)S = - \frac{22p_0h_1S}{63}$，
$T_2 \to T_3$降温过程中，等容变化，外界对气体做功$W_2 = 0$，
活塞受力平衡有$p_0S = f_0 + p_3S$，
解得封闭的理想气体压强$p_3 = \frac{20}{21}p_0$，
$T_3 \to T_4$降温过程中，等压压缩，由盖－吕萨克定律$\frac{h_2S}{T_3} = \frac{h_4S}{T_4}$，解得$h_4 = \frac{11}{10}h_1$，
外界对气体做功$W_3 = p_3(h_2 - h_4)S = \frac{2p_0h_1S}{9}$，
全过程中外界对气体做功$W = W_1 + W_2 + W_3 = - \frac{8p_0h_1S}{63}$，
因为$T_1 = T_4$，故封闭的理想气体总内能变化$\Delta U = 0$，
利用热力学第一定律$\Delta U = W + Q$，解得$Q = \frac{8p_0h_1S}{63}$，
故封闭气体吸收的净热量$Q = \frac{8p_0h_1S}{63}$.

压轴挑战 7 弹簧连接双活塞（2022·全国乙卷）如图，一竖直放置的汽缸由两个粗细不同的圆柱形筒组成，汽缸中活塞Ⅰ和活塞Ⅱ之间封闭有一定质量的理想气体，两活塞用一轻质弹簧连接，汽缸连接处有小卡销，活塞Ⅱ不能通过连接处。活塞Ⅰ、Ⅱ的质量分别为 $2m$、$m$，横截面积分别为 $2S$、$S$，弹簧原长为 $l$。初始时系统处于平衡状态，此时弹簧的伸长量为 $0.1l$，活塞Ⅰ、Ⅱ到汽缸连接处的距离相等，两活塞间气体的温度为 $T_0$。已知活塞外大气压强为 $p_0$，忽略活塞与汽缸壁间的摩擦，汽缸无漏气，不计弹簧的体积。
(1) 求弹簧的劲度系数；
(2) 缓慢加热两活塞间的气体，求当活塞Ⅱ刚运动到汽缸连接处时，活塞间气体的压强和温度。

答案： 7.题型分析
本题属于双塞单缸模型，第
(2)问要注意隐含条件的挖掘，从第
(1)问的受力分析中可知弹簧的弹力与封闭气体的压强无关，即在加热封闭气体时，弹簧并不会发生形变.
(1)$\frac{40mg}{l}$
(2)$\frac{3mg}{S} + p_0$$\frac{4}{3}T_0$
解析：
(1)对两活塞与弹簧整体进行受力分析得：$3mg + 2p_0S + p_0S = 2pS + p_0S$，
对活塞Ⅱ受力分析得：$p_0S + F = pS + mg$，
由胡克定律得：$F = 0.1kl$，
联立解得：$k = \frac{40mg}{l}$；
(2)通过对两活塞与弹簧整体进行受力分析得气体的压强$p = \frac{3mg}{S} + p_0$，可知气体做的是等压变化，那么弹簧上弹力大小不变，弹簧的长度不变，即两活塞间距离不变，
所以气体初态：体积$V_1 = (2S + S) · \frac{1.1}{2}l$，温度：$T_1 = T_0$，
末态：体积$V_2 = 2S · 1.1l$，温度为$T_2$，
由理想气体状态方程得：$\frac{V_1}{T_1} = \frac{V_2}{T_2}$，
联立解得$T_2 = \frac{4}{3}T_0$.
解题技巧：当题目中出现“缓慢加热”封闭气体的条件，且系统可以自由变化时，通常封闭气体要先做等压变化，类似于力学题中“缓慢移动”的条件，整个系统始终处于受力平衡的状态.
尽管活塞之间由弹簧或细绳连接，但对整体进行受力分析时，弹簧或细绳上的力作为内力并不考虑，整个系统的平衡状态由系统重力$mg$，大气压强$p_0$和封闭气体压强$p$共同决定，由于重力$mg$和大气压强$p_0$不变，所以封闭气体压强$p$也不改变，即在系统自由的情况下，缓慢加热封闭气体，封闭气体做等压变化，弹簧或细绳上的力也不变化，但当活塞在汽缸连接处被卡住之后，弹簧或细绳上的力就要发生变化.