第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
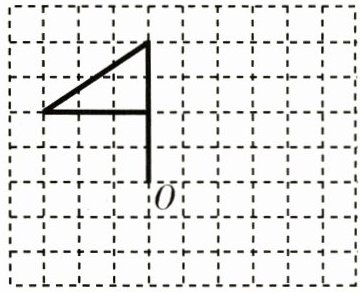
3. 在方格纸上按以下要求作图,不写作法.
(1)画出该图案向右平移$6$格后的图案;
(2)画出该图案绕点$O$逆时针旋转$90^{\circ}$后的图案.
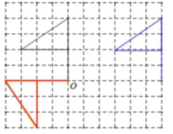
(1)画出该图案向右平移$6$格后的图案;
(2)画出该图案绕点$O$逆时针旋转$90^{\circ}$后的图案.

答案:

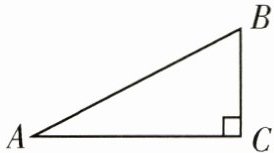
4. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$BC = 1$,$AC = \sqrt{5}$.
(1)将$\triangle ABC$绕点$B$逆时针旋转$90^{\circ}$后得到$\triangle A'BC'$,请画出旋转后的图形;
(2)求$AA'$的长.
(1)将$\triangle ABC$绕点$B$逆时针旋转$90^{\circ}$后得到$\triangle A'BC'$,请画出旋转后的图形;
(2)求$AA'$的长.

答案:
4.
(1)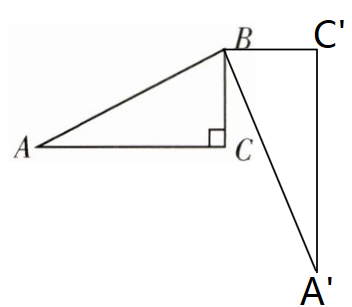
(2)2$\sqrt{3}$
4.
(1)

(2)2$\sqrt{3}$
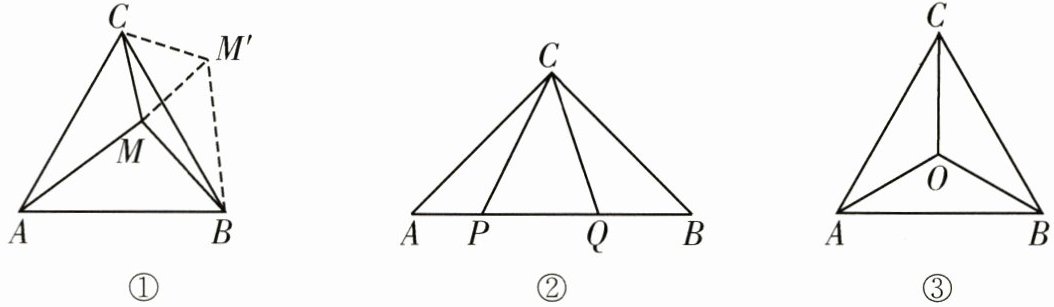
5. (1)【知识技能】如图①,在等边三角形$ABC$内有一点$M$.若点$M$到顶点$C$,$A$,$B$的距离分别为$6$,$10$,$8$,求$\angle BMC$的度数.
为了解决本题,我们可以将$\triangle AMC$绕顶点$C$逆时针旋转$60^{\circ}$到$\triangle BM'C$处,此时$\triangle BM'C\cong\triangle AMC$,这样就可以利用旋转变换,将三条线段$AM$,$BM$,$CM$转化到一个三角形中,则$\angle BMC$的度数是
(2)【构建联系】如图②,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC$,$P$,$Q$为$AB$上的点,且$\angle PCQ = 45^{\circ}$,求证:$PQ^{2} = BQ^{2} + AP^{2}$;
(3)【深入探究】如图③,在等边三角形$ABC$中,$AC = 2$,$O$为$\triangle ABC$内一点,连接$AO$,$BO$,$CO$,且$\angle AOC = \angle COB = \angle BOA = 120^{\circ}$,求$OA + OB + OC$的值.
为了解决本题,我们可以将$\triangle AMC$绕顶点$C$逆时针旋转$60^{\circ}$到$\triangle BM'C$处,此时$\triangle BM'C\cong\triangle AMC$,这样就可以利用旋转变换,将三条线段$AM$,$BM$,$CM$转化到一个三角形中,则$\angle BMC$的度数是
150°
;(2)【构建联系】如图②,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC$,$P$,$Q$为$AB$上的点,且$\angle PCQ = 45^{\circ}$,求证:$PQ^{2} = BQ^{2} + AP^{2}$;
(3)【深入探究】如图③,在等边三角形$ABC$中,$AC = 2$,$O$为$\triangle ABC$内一点,连接$AO$,$BO$,$CO$,且$\angle AOC = \angle COB = \angle BOA = 120^{\circ}$,求$OA + OB + OC$的值.

答案:
5
(1)150°
(2)证明:如图①,把△APC绕点C逆时针旋转90°得到△BP'C,连接P'Q.由旋转的性质得CP'=CP,BP'=AP,∠CBP'=∠A,∠PCP'=90°.
∵∠PCQ=45°,
∴∠P'CQ=∠P'CP - ∠PCQ=45°.
∴∠PCQ=∠P'CQ.在△PCQ和△P'CQ中,
$\begin{cases} CP = CP' \\ \angle PCQ = \angle P'CQ \end{cases}$
∴△PCQ≌△P'CQ(SAS).
∴PQ = P'Q.
∵∠ACB=90°,AC=BC,
∴∠CBP'=∠A=∠ABC=45°.
∴∠P′BQ=∠CBP'+∠ABC=90°.
∴P'Q²=BQ²+BP'²,即PQ²=BQ²+AP².
(3)解:


如图②,将△COB绕点B顺时针旋转60°,得到△C'O'B,连接OO',则O'C'=OC,O'B=OB,BC'=BC=AC=2,∠OBO'=∠CBC'=60°,∠BO'C'=∠COB,
∴∠C'BA=∠ABC+∠CBC'=120°,△BOO'是等边三角形.
∴OB=OO',∠BOO′=∠BO'O=60°.
∵∠AOC=∠COB=∠BOA=120°,
∴∠BOA+∠BOO'=∠BO'C'+∠BO'O=120°+60°=180°.
∴A,O,O',C'四点共线.过点C'作C'H⊥AB交AB延长线于点H,则∠H=90°,
∴∠C'BH=180° - ∠C'BA=60°,则∠BC'H=90° - ∠C'BH=30°.
∴BH=$\frac{1}{2}$BC'=1,C'H=$\sqrt{BC'^2 - BH^2}$=$\sqrt{3}$.在Rt△AHC'中,AH=AB+BH=3,
∴AC'=$\sqrt{AH^2 + C'H^2}$=2$\sqrt{3}$
∴OA+OB+OC=OA+OO'+O'C'=AC'=2$\sqrt{3}$
5
(1)150°
(2)证明:如图①,把△APC绕点C逆时针旋转90°得到△BP'C,连接P'Q.由旋转的性质得CP'=CP,BP'=AP,∠CBP'=∠A,∠PCP'=90°.
∵∠PCQ=45°,
∴∠P'CQ=∠P'CP - ∠PCQ=45°.
∴∠PCQ=∠P'CQ.在△PCQ和△P'CQ中,
$\begin{cases} CP = CP' \\ \angle PCQ = \angle P'CQ \end{cases}$
∴△PCQ≌△P'CQ(SAS).
∴PQ = P'Q.
∵∠ACB=90°,AC=BC,
∴∠CBP'=∠A=∠ABC=45°.
∴∠P′BQ=∠CBP'+∠ABC=90°.
∴P'Q²=BQ²+BP'²,即PQ²=BQ²+AP².
(3)解:


如图②,将△COB绕点B顺时针旋转60°,得到△C'O'B,连接OO',则O'C'=OC,O'B=OB,BC'=BC=AC=2,∠OBO'=∠CBC'=60°,∠BO'C'=∠COB,
∴∠C'BA=∠ABC+∠CBC'=120°,△BOO'是等边三角形.
∴OB=OO',∠BOO′=∠BO'O=60°.
∵∠AOC=∠COB=∠BOA=120°,
∴∠BOA+∠BOO'=∠BO'C'+∠BO'O=120°+60°=180°.
∴A,O,O',C'四点共线.过点C'作C'H⊥AB交AB延长线于点H,则∠H=90°,
∴∠C'BH=180° - ∠C'BA=60°,则∠BC'H=90° - ∠C'BH=30°.
∴BH=$\frac{1}{2}$BC'=1,C'H=$\sqrt{BC'^2 - BH^2}$=$\sqrt{3}$.在Rt△AHC'中,AH=AB+BH=3,
∴AC'=$\sqrt{AH^2 + C'H^2}$=2$\sqrt{3}$
∴OA+OB+OC=OA+OO'+O'C'=AC'=2$\sqrt{3}$
查看更多完整答案,请扫码查看


