第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
2. 如图,以 $ (1,-4) $ 为顶点的二次函数 $ y = ax^{2}+bx + c $ 的图象与 $ x $ 轴负半轴交于 $ A $ 点,则一元二次方程 $ ax^{2}+bx + c = 0 $ 的正数解的取值范围是(
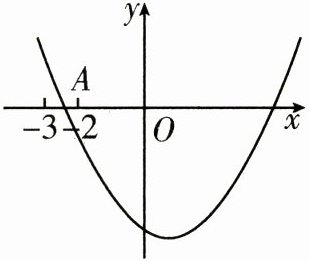
A.$ 2 < x < 3 $
B.$ 3 < x < 4 $
C.$ 4 < x < 5 $
D.$ 5 < x < 6 $
C
).
A.$ 2 < x < 3 $
B.$ 3 < x < 4 $
C.$ 4 < x < 5 $
D.$ 5 < x < 6 $
答案:
C
1. 二次函数 $ y = ax^{2}+bx + c $ 的部分图象如图所示,该函数图象的对称轴是直线 $ x = 1 $,图象与 $ y $ 轴交点的纵坐标是 2. 有下列结论:① $ 2a + b = 0 $;②方程 $ ax^{2}+bx + c = 0 $ 一定有一个根在 $ -2 $ 和 $ -1 $ 之间;③方程 $ ax^{2}+bx + c-\frac{3}{2}=0 $ 一定有两个不等的实数根;④ $ b - a < 2 $. 其中正确的结论有(

A.1 个
B.2 个
C.3 个
D.4 个
B
).
A.1 个
B.2 个
C.3 个
D.4 个
答案:
B
2. 已知二次函数 $ y = x^{2}-3x + m $($ m $ 为常数)的图象与 $ x $ 轴的一个交点为 $ (1,0) $,则关于 $ x $ 的一元二次方程 $ x^{2}-3x + m = 0 $ 的两个实数根分别是(
A.$ x_{1}=1 $,$ x_{2}=-1 $
B.$ x_{1}=1 $,$ x_{2}=2 $
C.$ x_{1}=1 $,$ x_{2}=0 $
D.$ x_{1}=1 $,$ x_{2}=3 $
B
).A.$ x_{1}=1 $,$ x_{2}=-1 $
B.$ x_{1}=1 $,$ x_{2}=2 $
C.$ x_{1}=1 $,$ x_{2}=0 $
D.$ x_{1}=1 $,$ x_{2}=3 $
答案:
B
3. 若抛物线 $ y = x^{2}+bx + c $ 与 $ x $ 轴只有一个交点,且过点 $ A(m,n) $,$ B(m + 6,n) $,则 $ n = $
9
.
答案:
9
查看更多完整答案,请扫码查看


