第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1. 有一座抛物线形拱桥的示意图如图所示,正常水位时,桥下水深6m,水面宽度为20m,拱顶距离水平面4m.为保证过往船只顺利航行,桥下水面宽度不得小于18m,且当水深超过某数值时,就会影响过往船只的顺利航行,则该数值为(
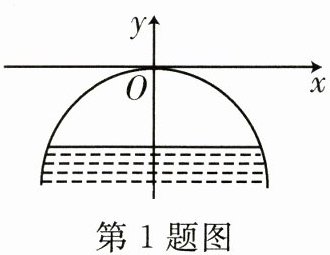
A.2.76m
B.6.76m
C.6m
D.7m
B
).
A.2.76m
B.6.76m
C.6m
D.7m
答案:
1. B
2. 校运会期间,某学校在运动场入口安装了一座充气拱门,拱门呈抛物线状(如图所示).数学小组想了解拱门的高度,先测量拱门底端距离$AB=8$m,再用两根长度为2m的标杆CE,DF垂直于地面且让标杆端点C,D在拱门上,再测量出两标杆间的距离$EF=6$m,则此拱门(不考虑拱门自身的粗细大小)的高度为(
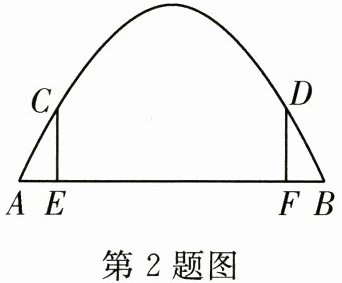
A.6m
B.4.8m
C.$\frac{32}{7}$m
D.$\frac{18}{7}$m
C
).
A.6m
B.4.8m
C.$\frac{32}{7}$m
D.$\frac{18}{7}$m
答案:
2. C
3. 某座下沿呈抛物线形的廊桥示意图如图所示,已知抛物线的函数解析式为$y=-\frac{1}{40}x^2+10$.为保护廊桥的安全,在该抛物线上距水面AB高为8m的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是

8$\sqrt{5}$
m.
答案:
3. 8$\sqrt{5}$
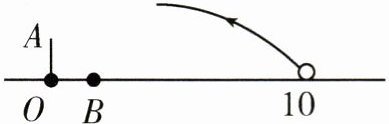
4. 如图,在某场足球比赛中,球员甲从球门底部中点O的正前方10m处起脚射门,足球沿抛物线飞向球门中线.当足球飞离地面高度为3m时到达最高点,此时足球飞行的水平距离为6m.已知球门的横梁高OA为2.44m.
(1)球员甲能否进球? (不计其他情况)
(2)守门员乙站在距离球门2m的B处,他跳起时手最高能达到2.52m,他能拦下足球吗? 如果不能,那么他至少后退多远才能拦下足球?
(1)球员甲能否进球? (不计其他情况)
(2)守门员乙站在距离球门2m的B处,他跳起时手最高能达到2.52m,他能拦下足球吗? 如果不能,那么他至少后退多远才能拦下足球?

答案:
4. 解:
(1)以O为坐标原点,以OB所在直线为x轴,以OA所在直线为y轴建立平面直角坐标系. 抛物线的顶点坐标是(4,3),设抛物线的解析式是y = a(x - 4)² + 3. 把点(10,0)代入,得36a + 3 = 0,解得a = −$\frac{1}{12}$,则抛物线的解析式为y = −$\frac{1}{12}$(x - 4)² + 3. 当x = 0时,y = −$\frac{1}{12}$×16 + 3 = 3 - $\frac{4}{3}$ = $\frac{5}{3}$<2.44,答:球员甲能进球.
(2)当x = 2时,y = −$\frac{1}{12}$×(2 - 4)² + 3 = $\frac{8}{3}$>2.52,
∴守门员乙不能拦下足球. 令y = 2.52,得−$\frac{1}{12}$(x - 4)² + 3 = 2.52,解得x₁ = 1.6,x₂ = 6.4(舍去).
∴2 - 1.6 = 0.4(m). 答:守门员乙至少要后退0.4 m才能拦下足球.
(1)以O为坐标原点,以OB所在直线为x轴,以OA所在直线为y轴建立平面直角坐标系. 抛物线的顶点坐标是(4,3),设抛物线的解析式是y = a(x - 4)² + 3. 把点(10,0)代入,得36a + 3 = 0,解得a = −$\frac{1}{12}$,则抛物线的解析式为y = −$\frac{1}{12}$(x - 4)² + 3. 当x = 0时,y = −$\frac{1}{12}$×16 + 3 = 3 - $\frac{4}{3}$ = $\frac{5}{3}$<2.44,答:球员甲能进球.
(2)当x = 2时,y = −$\frac{1}{12}$×(2 - 4)² + 3 = $\frac{8}{3}$>2.52,
∴守门员乙不能拦下足球. 令y = 2.52,得−$\frac{1}{12}$(x - 4)² + 3 = 2.52,解得x₁ = 1.6,x₂ = 6.4(舍去).
∴2 - 1.6 = 0.4(m). 答:守门员乙至少要后退0.4 m才能拦下足球.
查看更多完整答案,请扫码查看


