《2025年同步练习册泰山出版社七年级数学上册青岛版》

17. (10 分)计算
(1)$-\frac{1}{5} × [-5^2 + 3 ÷ (-\frac{1}{3})^2] - 1.5^2$。
(2)$-2^2 ÷ \frac{2}{3} × (-\frac{2}{3} + 1)^2$。

答案： $(1)$ 计算$-\frac{1}{5} × [-5^2 + 3 ÷ (-\frac{1}{3})^2] - 1.5^2$
解：
根据运算顺序，先算乘方：
$-5^2=-25$，$(-\frac{1}{3})^2=\frac{1}{9}$，$1.5^2 = (\frac{3}{2})^2=\frac{9}{4}$。
再算括号内的除法：$3÷\frac{1}{9}=3×9 = 27$。
然后算括号内的加法：$-25 + 27=2$。
接着算乘法：$-\frac{1}{5}×2=-\frac{2}{5}$。
最后算减法：$-\frac{2}{5}-\frac{9}{4}=-\frac{8}{20}-\frac{45}{20}=-\frac{53}{20}=-2.65$。
$(2)$ 计算$-2^2 ÷ \frac{2}{3} × (-\frac{2}{3} + 1)^2$
解：
先算乘方：$-2^2=-4$，$(-\frac{2}{3} + 1)^2=(\frac{1}{3})^2=\frac{1}{9}$。
再算除法：$-4÷\frac{2}{3}=-4×\frac{3}{2}=-6$。
最后算乘法：$-6×\frac{1}{9}=-\frac{2}{3}$。
综上，答案依次为$(1)$$-2.65$；$(2)$$-\frac{2}{3}$。

18. (8 分)在数轴上表示下列各数：$2.5$,$-3.5$,$-|-2|$,$0$,$-(-4)$,$-\frac{1}{3}$,并用“$＜$”把这些数连接起来。

答案：
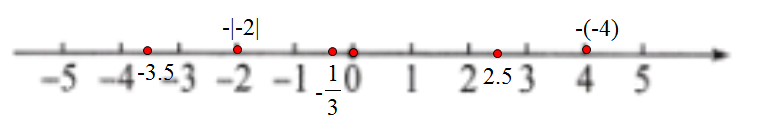
$-3.5＜-|-2|＜-\frac{1}{3}＜0＜2.5＜-(-4)$ 数轴如图所示

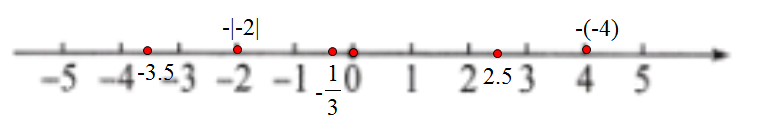
19. (8 分)某自行车厂一周计划生产 700 辆自行车,平均每天生产自行车 100 辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入,下表是某周的自行车生产情况：(超过计划生产量为正,不足计划生产量为负,单位：辆)

(1)根据记录求前三天共生产自行车多少辆；
(2)若该厂实行日计件工资制,每生产一辆自行车可得 60 元,一天中生产超过计划生产量的,每超一辆奖 15 元,一天中生产不足计划生产量的,每少一辆扣 20 元,那么该厂工人这一周的工资总额是多少？

答案： 1. （1）
解：已知平均每天计划生产$100$辆，根据前三天的增减情况：
星期一生产$(100 + 6)$辆，星期二生产$(100−2)$辆，星期三生产$(100−4)$辆。
则前三天共生产：$(100 + 6)+(100−2)+(100−4)$
利用加法交换律和结合律$=(100 + 100+100)+(6−2−4)$
因为$100 + 100+100 = 300$，$6−2−4 = 0$，所以前三天共生产$300$辆。
2. （2）
解：
先计算一周实际生产的辆数：
一周计划生产$700$辆，实际生产的增减量为$( + 6)+(−2)+(−4)+( + 10)+(−9)+( + 10)+(−11)$
$=(6 + 10+10)+(-2−4−9−11)$
$=26+( - 26)$
$=0$，所以实际生产$700$辆。
再计算工资总额：
每生产一辆得$60$元，所以生产工资为$700×60 = 42000$元。
计算奖金和扣钱数：
奖金：$(6 + 10+10)×15$
$=26×15$
$=390$元。
扣钱数：$(2 + 4+9+11)×20$
$=26×20$
$=520$元。
工资总额$=$生产工资$+$奖金$-$扣钱数，即$42000+390 - 520$
$=42000-(520 - 390)$
$=42000 - 130$
$=41870$元。
综上，（1）前三天共生产自行车$300$辆；（2）该厂工人这一周的工资总额是$41870$元。

20. (8 分)如图所示是一个长方形。
(1)根据图中尺寸大小,用含 $x$ 的代数式表示阴影部分的面积 $S$；
(2)若 $x = 3$,求 $S$ 的值。

答案： 解：
(1)$S=\frac 12×4×8-\frac 12×(8-4)×(4-x)=16-8+2x=2x+8(cm^2)$
(2)当x=3时，$S=2×3+8=14(cm^2)$